9类RD Sharma解决方案–第15章平行四边形和三角形的区域-练习15.3 |套装3

问题21.在图中，PSDA是一个平行四边形，其中PQ = QR = RS，AP || BQ || CR。证明ar(ΔPQE)= ar(ΔCFD)。

解决方案：

According to the question

PSDA is a parallelogram

So, AP || BQ || CR || DS and AD || PS

PQ = CD       …..(i)

Prove that (ΔPQE) = ar(ΔCFD)

Proof:

In ΔBED, 

C is the midpoint of BD and CF || BE

So, F is the midpoint of ED

Hence, EF = PE

Similarly, EF = PE

Therefore, PE = FD             …..(ii)

In ΔPQE and CFD,

PE = FD

∠ EPQ = ∠FDC                            (Alternate angles)

PQ = CD

So, by SAS congruence, we have

ΔPQE ≅ ΔDCF

Hence, ar(ΔPQE) = ar(ΔDCF)

问题22.从图中看，ABCD是一个梯形，其中AB || DC和DC = 40厘米，AB = 60厘米。如果X和Y分别是AD和BC的中点，则证明：

(i)XY = 50厘米

(ii)DCYX是梯形

(iii)ar(陷阱DCYX)=(9/11)ar(XYBA)。

解决方案：

(i) Join DY and produce it to meet AB produced at P.

In ΔBYP and CYD 

∠BYP = ∠ CYD          (Vertically opposite angles)

∠DCY = ∠ PBY           (As, DC || AP)

BY = CY

So, by ASA congruence, 

ΔBYP ≅ ΔCYD

By C.P.C.T

DY = YP and DC = BP

As we know that, Y is the midpoint of DP

also, X is the midpoint of AD

So, XY || AP and XY || (1/2) AP

XY = (1/2) (AB + BP)

XY = (1/2) (AB + DC)

XY = (1/2) (60 + 40) = 50 cm

(ii) Given that, 

XY || AP

XY || AB and AB || DC

XY || DC

Hence, DCYX is a trapezium

(iii) As we know that X and Y are the mid-points of Ad and BC.

So, trapezium DCYX and ABYX are of the same height 

Let us assume, the height of the trapezium is h cm

Now,

ar(trap. DCXY) = (1/2)(DC + XY) × h

ar(trap. DCXY) = (1/2) (50 + 40) × h cm² = 45 h cm²

ar(trap. ABYX) = (1/2)(AB + XY) × h

ar(trap. ABYX) = (1/2)(60 + 50) × h cm² = 55h cm²

ar(trap. DCYX) ar(trap. ABYX) = 45h/55h = 9/11

Hence, ar(trap. DCYX) = 9/11 ar(trap. ABYX)

问题23。在图中，ABC和BDE是两个等边三角形，使得D是BC的中点。 AE在F中与BC相交。证明：

(i)ar(ΔBDE)=(1/4)ar(ΔABC)

(ii)ar(ΔBDE)=(1/2)ar(ΔBAE)

(iii)ar(ΔBFE)= ar(ΔAFD)

(iv)ar(ΔABC)= 2 ar(ΔBEC)

(v)ar(ΔFED)= 1/8 ar(ΔAFC)

(vi)ar(ΔBFE)= 2 ar(ΔEFD)

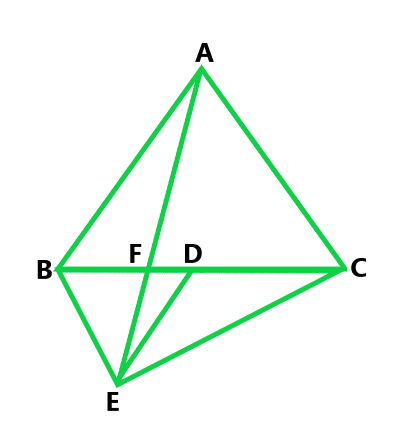
解决方案：

According to the question

ABC and BDE are two equilateral triangles.

Let us considered AB = BC = CA = x. Then, BD = x/2 = DE = BE

(i) Given that,

ar(ΔABC) = √3/4 x² ….(i)

ar(ΔBDE) = √3/4 (x/2)² = 1/4 x √3/4 x²

Now put the value of √3/4 x² from eq(i), we get

Hence, ar(ΔBDE) = 1/4 ar(ΔABC)

Hence proved

(ii) Given that, 

ΔABC and BED are equilateral triangles

So, ∠ ACB = ∠DBE = 60°

BE || AC                                    (Alternative angles are equal)

As we know that ΔBAF and ΔBEC are on the same base BE 

and between same parallels BF and AC.

So, ar(ΔBAE) = ar(ΔBEC)

ED is a median of ΔEBC

So, ar(ΔBAE) = 2ar(ΔBDE)                      

Hence, ar(ΔBDE) = (1/2) ar(ΔBAE)

(iii) Given that,

ΔABC and BDE are equilateral triangles

So, ∠ABC = 60° and ∠BDE = 60°

∠ABC = ∠BDE

AB || DE                   (Alternate angles are equal)

As we know that ΔBED and ΔAED are on the same base ED and 

between same parallels AB and DE.

So, ar(ΔBED) = ar(ΔAED)

ar(ΔBED) − ar(ΔEFD) = ar(ΔAED) − ar(ΔEFD)

Hence, ar(ΔBEF) = ar(ΔAFD)

(iv) Given that,

ED is the median of tΔBEC

So, ar(ΔBEC) = 2ar(ΔBDE)

ar(ΔBEC) = 2 × (1/2) ar(ΔABC)    (Proved above)              

ar(ΔBEC) = (1/2) ar(ΔABC)

Hence, ar(ΔABC) = 2ar(ΔBEC)

(v) ar(ΔAFC) = ar(ΔAFD) + ar(ΔADC)

ar(ΔBFE) + (1/2) ar(ΔABC)                       

ar(ΔBFE) + (1/2) × 4ar(ΔBDE)             

ar(ΔBFE) = 2ar(ΔFED)  …..(iii)

ar(ΔBDE) = ar(ΔBFE) + ar(ΔFED)

2ar(ΔFED) + ar(ΔFED)

3ar(ΔFED)         ….(iv)

From eq (ii), (iii) and (iv), we get

ar(ΔAFC) = 2ar(ΔFED) + 2 × 3 ar(ΔFED) = 8 ar(ΔFED)

Hence, ar(ΔFED) = (1/8) ar(ΔAFC)

(vi) Let’s assume that h be the height of vertex E, corresponding to the side BD in ΔBDE and

H be the height of vertex A, corresponding to the side BC in ΔABC

As we proved above

ar(ΔBDE) = (1/4) ar(ΔABC)

(1/2) × BD × h = (1/4) (1/2 × BC × h)

BD × h = (1/4)(2BD × H)

h = (1/2) H    ….(i)

From part (iii), we get

ar(ΔBFE) = ar(ΔAFD)

ar(ΔBFE) = (1/2) × FD × H

ar(ΔBFE) = (1/2) × FD × 2h

ar(ΔBFE) = 2((1/2) × FD × h)

Hence, ar(ΔBFE) = 2ar(ΔEFD)

问题24. D是ΔABC的BC边的中点，E是BD的中点。如果O是AE的中点，则证明ar(ΔBOE)=(1/8)ar(ΔABC)。

解决方案：

According to the question

D is the midpoint of sides BC of Δ ABC,

E is the midpoint of BD and O is the midpoint of AE,

So, AD and AE are the medians of ΔABC and ΔABD 

Hence, ar(ΔABD) = (1/2) ar(ΔABC)   …..(i)

and ar(ΔABE) = (1/2) ar(ΔABD)   …….(ii)

Also, OB is the median of triangle ABE

So, ar(ΔBOE) = (1/2) ar(ΔABE)

From eq (i), (ii) and (iii), we conclude that

ar(ΔBOE) = (1/8) ar(ΔABC)

Hence proved

问题25.在图中，X和Y分别是AC和AB的中点，QP || BC，CYQ和BXP是直线。证明ar(ΔABP)= ar(ΔACQ)。

解决方案：

According to the question

X and Y are the mid-points of AC and AB 

So, XY || BC

Prove: ar(ΔABP) = ar(ΔACQ)

Proof:

From the figure, we conclude that ΔBYC and BXC are on the same base BC and 

between the same parallels XY and BC

So, ar(ΔBYC) = ar(ΔBXC)

ar(ΔBYC) − ar(ΔBOC) = ar(ΔBXC) − ar(ΔBOC)

ar(ΔBOY) = ar(ΔCOX)

ar(ΔBOY) + ar(ΔXOY) = ar(ΔCOX) + ar(ΔXOY)

ar(ΔBXY) = ar(ΔCXY)             …..(i)

From the figure we conclude that the quadrilaterals XYAP and XYAQ are on 

the same base XY and between same parallels XY and PQ.

So, ar(quad. XYAP) = ar(quad XYQA)   ….(ii)

Now, add eq(i) and (ii), we get

ar(ΔBXY) + ar(quad. XYAP) = ar(ΔCXY) + ar(quad XYQA)

 ar(ΔABP) = ar(ΔACQ)

Hence proved

问题26.在图中，ABCD和AEFD是两个平行四边形。证明

(i)PE = FQ

(ii)ar(ΔAPE)：ar(ΔPFA)= ar(ΔQFD)：ar(ΔPFD)

(iii)ar(ΔPEA)= ar(ΔQFD)

解决方案：

According to the question

ABCD and AEFD are two parallelograms

(i) Prove that PE = FQ

Proof:

In ΔEPA and FQD

∠PEA = ∠QFD         (Corresponding angles)

∠EPA=∠FQD           (Corresponding angles)

PA = QD                   (Opposite sides of parallelogram)

So, by AAS congruence

ΔEPA ≅ ΔFQD       

Hence, by C.P.C.T

EP = FQ               

Hence proved

(ii) Prove that ar(ΔAPE) : ar(ΔPFA) = ar(ΔQFD) : ar(ΔPFD)

From the figure we conclude that ΔPEA and ΔQFD stand on equal bases 

PE and FQ lies between the same parallels EQ and AD

So, ar(ΔPEA) = ar(ΔQFD) ……(i)

From the figure we conclude that ΔPEA and ΔPFD stand on the same 

base PF and between same parallels PF and AD

Therefore, ar(ΔPFA) = ar(ΔPFD)      ……(ii)

Now divide eq(i) by eq(ii), we get

Hence, ar(ΔPEA) : ar(ΔPFA) = ar(ΔQFD) : ar(ΔPFD)

Hence proved

(iii) Prove that ar(ΔPEA) = ar(ΔQFD)

Proof:

As we proved above that

ΔEPA ≅ ΔFQD

Hence, ar(ΔPEA) = ar(ΔQFD)

Hence proved

问题27.在图中，ABCD是平行四边形。 O是AC上的任意点。 PQ || AB和LM ||广告。证明：ar(|| gm DLOP)= ar(|| gm BMOQ)。

解决方案：

According to the question

ABCD is a parallelogram and PQ || AB and LM || AD

Prove that ar(||gm DLOP) = ar(||gm BMOQ)

Proof:

Here, the diagonal AC of a parallelogram divides it into two triangles of equal area

So, ar(ΔADC) = ar(ΔABC)

ar(ΔAPO) + ar(||gm DLOP) + ar(ΔOLC)

ar(ΔAOM) + ar(||gm BMOQ) + ar(ΔOQC)           ……(i)

From the figure, AO and OC are diagonals of parallelograms AMOP and OQCL

So, ar(ΔAPO) = ar(ΔAMO)             ……(ii)

And ar(ΔOLC) = ar(ΔOQC)            ……(iii)

Now subtracting eq(ii) and (iii) from (i), we get

ar(||gm DLOP) = ar(||gm BMOQ)

Hence proved

问题28.在三角形ABC中，如果L和M分别是AB和AC上的点，则LM ||公元前。证明：

(i)ar(ΔLCM)= ar(ΔLBM)

(ii)ar(ΔLBC)= ar(ΔMBC)

(iii)ar(ΔABM)= ar(ΔACL)

(iv)ar(ΔLOB)= ar(ΔMOC)

解决方案：

According to the question

ABC is a triangle and L and M are points on AB and AC respectively such that LM || BC

(i) Here, Δ LMB and LMC are on the same base LM and between the same parallels LM and BC.

Hence, ar(ΔLMB) = ar(ΔLMC)            

(ii) Here, ΔLBC and MBC are on the same base BC and between same parallels LM and BC.

Hence, ar(ΔLBC) = ar(ΔMBC)         

(iii) Here, we have

ar(ΔLMB) = ar(ΔLMC)            (Proved above)

ar(ΔALM) + ar(ΔLMB) = ar(ΔALM) + ar(ΔLMC)

Hence, ar(ΔABM) = ar(ΔACL)

(iv) Here, we have

ar(ΔLBC) = ar(ΔMBC)              (Proved above)

ar(ΔLBC) − ar(ΔBOC) = ar(ΔMBC) − ar(ΔBOC)

Hence, ar(ΔLOB) = ar(ΔMOC).

问题29.在图中，D和E是BC上的两个点，因此BD = DE = EC。证明ar(ΔABD)= ar(ΔADE)= ar(ΔAEC)。

解决方案：

In the triangle ABC, draw a line || through A parallel to BC.

BD = DE = EC  (Given)

Now from the figure, triangles ABD and AEC are on the same base AC and 

between the same parallels l and BC. Hence, the area of triangles ABD and AEC is equal.

Hence, ar(ΔABD) = ar(ΔADE) = ar(ΔAEC).

问题30.在图中，ABC是A处的直角三角形，BCED，ACFG和ABMN分别是BC，CA和AB侧的正方形。线段AX⊥DE在Y遇见BC。

(i)ΔMBC≅ΔABD

(ii)ar(BYXD)= 2ar(ΔMBC)

(iii)ar(BYXD)= ar(ABMN)

(iv)ΔFCB≅ΔACE

(v)ar(CYXE)= 2ar(ΔFCB)

(vi)ar(CYXE)= ar(ACFG)

(vii)ar(BCED)= ar(ABMN)+ ar(ACFG)

解决方案：

According to the question

ABC is a right-angled triangle at A, BCED, ACFG, and ABMN are squares on the sides BC, CA, and AB 

(i) In ΔMBC and ΔABD, 

MB = AB,

BC = BD,

∠MBC = ∠ABD             

So, by SAS congruence, we have

ΔMBC ≅ ΔABD

Hence, ar(ΔMBC) = ar(ΔABD)   

(ii) From the figure, triangle ABC and rectangle BYXD are on the same base BD 

and between the same parallels AX and BD.

So, ar(ΔABD) = (1/2) ar(rect BYXD)

ar(rect BYXD) = 2ar(ΔABD)

From part (i)

Hence, ar(rect BYXD) = 2ar(ΔMBC)   ……(i)        

(iii) From the figure, triangles MBC and square MBAN are on the same base MB and 

between the same parallels MB and NC.

So, 2ar(ΔMBC) = ar(MBAN)  ……(ii)

From eq(i) and (ii), we get

Hence, ar(sq. MBAN) = ar(rect BYXD)

(iv) In ΔFCB and ACE, 

FC = AC

CB = CE

∠FCB = ∠ACE               

So, by SAS congruence, 

Hence, ΔFCB ≅ ΔACE

(v) As we proved above

ΔFCB ≅ ΔACE

So, ar(ΔFCB) = ar(ΔACE)

From the figure, triangle ACE and rectangle CYXE are on the same base CE 

and between same parallels CE and AX.

So, 2ar(ΔACE) = ar(CYXE)

Hence, 2ar(ΔFCB) = ar(ΔCYXE)        …..(iii)

(vi) From the figure, triangle FCb and rectangle FCAG are on the same base FC 

and between the same parallels FC and BG.

So, 2ar(ΔFCB) = ar(FCAG)            ……(iv)

From eq(iii) and (iv), we get

ar(CYXE) = ar(ACFG)

(vii) In ΔACB, we have

Using Pythagoras theorem 

BC² = AB² + AC²

BC × BD = AB × MB + AC × FC

Hence, ar(BCED) = ar(ABMN) + ar(ACFG)