问题1.通过完成平方的方法,找到以下二次方程式的根(如果存在):
(i)2x 2 – 7x + 3 = 0
解决方案:
2x2 – 7x = – 3
Dividing by 2 on both sides, we get
x2 –![]() = –
= –![]()
x2 -2 × x ×![]() = –
= –![]()
On adding (![]() )2 to both sides of equation, we get
)2 to both sides of equation, we get
(x)2 – 2×x×![]() +(
+(![]() )2 = (
)2 = (![]() )2–
)2–![]()
(x-![]() )2 = (
)2 = (![]() ) – (
) – (![]() ) (Using identity: a2 – 2ab + b2 = (a-b)2)
) (Using identity: a2 – 2ab + b2 = (a-b)2)
(x-![]() )2 =
)2 =![]()
(x-![]() )2 = ±
)2 = ±![]()
x =![]()
x =![]() or x =
or x =![]()
x =![]() or x =
or x =![]()
x = 3 or x =![]()
(ii)2x 2 + x – 4 = 0
解决方案:
2x2 + x = 4
Dividing both sides of the equation by 2, we get
x2 +![]() = 2
= 2
Now on adding![]() 2 to both sides of the equation, we get,
2 to both sides of the equation, we get,
(x)2 + 2 × x ×![]() + (
+ (![]() )2 = 2 + (
)2 = 2 + (![]() )2
)2
(x +![]() )2 =
)2 =![]() (Using identity: a2 + 2ab + b2 = (a+b)2)
(Using identity: a2 + 2ab + b2 = (a+b)2)
x +![]() = ±
= ±![]()
x =![]()
x =![]()
Hence, x =![]() or x =
or x =![]()
(iii)4x 2 +4√3x+ 3 = 0
解决方案:
4x2 + 4√3x = -3
Dividing both sides of the equation by 4, we get
x2 + √3x = –![]()
Now on adding (![]() )2 to both sides of the equation, we get,
)2 to both sides of the equation, we get,
(x)2 + 2 × x ×![]() + (
+ (![]() )2 = –
)2 = –![]() + (
+ (![]() )2
)2
(x +![]() )2 = 0 (Using identity: a2 + 2ab + b2 = (a+b)2)
)2 = 0 (Using identity: a2 + 2ab + b2 = (a+b)2)
Hence, x = –![]() or x = –
or x = –![]()
(iv)2x 2 + x + 4 = 0
解决方案:
2x2 + x = -4
Dividing both sides of the equation by 2, we get
x2 +![]() = -2
= -2
Now on adding (![]() )2 to both sides of the equation, we get,
)2 to both sides of the equation, we get,
(x)2 + 2 × x ×![]() + (
+ (![]() )2 = – 2 + (
)2 = – 2 + (![]() )2
)2
(x +![]() )2 =
)2 =![]() (Using identity: a2 + 2ab + b2 = (a+b)2)
(Using identity: a2 + 2ab + b2 = (a+b)2)
As we know, the square of numbers cannot be negative.
Hence, there is no real root for the given equation, 2x2 + x + 4 = 0.
问题2。通过应用二次方程式,找到上述Q.1中给出的二次方程式的根。
(i)2x 2 – 7x + 3 = 0
解决方案:
On comparing the equation with ax2 + bx + c = 0, we get,
a = 2, b = -7 and c = 3
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
x =![]()
x =![]() or x =
or x =![]()
x =![]() or
or![]()
x = 3 or![]()
(ii)2x 2 + x – 4 = 0
解决方案:
On comparing the equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = -4
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
x =![]() or x =
or x =![]()
(iii)4x 2 +4√3x+ 3 = 0
解决方案:
On comparing the equation with ax2 + bx + c = 0, we get,
a = 4, b = 4√3 and c = 3
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
x =![]() or x =
or x =![]()
(iv)2x 2 + x + 4 = 0
解决方案:
On comparing the equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = 4
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
As we know, the square of a number can never be negative.
Hence, there is no real solution for the given equation.
问题3.找到以下方程式的根:
(i)x –  = 3,x≠0
= 3,x≠0
解决方案:
After rearranging, we get
x2 – 3x -1 = 0
On comparing the equation with ax2 + bx + c = 0, we get,
a = 1, b = -3 and c = -1
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
x =![]() or x =
or x =![]()
(ii) 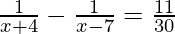 ,x≠-4,7
,x≠-4,7
解决方案:
![]()
![]()
After rearranging,
(x+4)(x-7) = -30
x2 – 3x – 28 = 30
x2 – 3x + 2 = 0
On comparing the equation with ax2 + bx + c = 0, we get,
a = 1, b = -3 and c = 2
Then roots of the quadratic equation =![]()
x =![]()
x =![]()
x =![]()
x =![]()
x =![]() or x =
or x =![]()
x = 2 or x = 1
问题4。3年前和5年后的雷曼年龄的倒数之和(以年为单位)是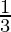 。找到他现在的年龄。
。找到他现在的年龄。
解决方案:
Let’s take,
Present age of Rehman is x years.
Three years ago, Rehman’s age was (x – 3) years.
Five years after, his age will be (x + 5) years.
According to the given condition,
![]()
![]()
![]()
3(2x + 2) = (x-3)(x+5)
6x + 6 = x2 + 2x – 15
x2 – 4x – 21 = 0
x2 – 7x + 3x – 21 = 0 (by factorizing)
x(x – 7) + 3(x – 7) = 0
(x – 7)(x + 3) = 0
x = 7, -3
As, age cannot be negative.
Therefore, Rehman’s present age is 7 years.
问题5:在课堂测试中,Shefali在数学和英语中的分数总和为30。如果她在数学中获得2分,而在英语中少得到3分,则它们的分数乘积应为210。两个科目。
解决方案:
Let’s take,
The marks of Shefali in Maths be x.
Then, the marks in English will be 30 – x.
According to the given condition,
(x + 2)(30 – x – 3) = 210
(x + 2)(27 – x) = 210
-x2 + 25x + 54 = 210
Multiply the equation by (-1),
x2 – 25x + 156 = 0
x2 – 12x – 13x + 156 = 0
x(x – 12) -13(x – 12) = 0
(x – 12)(x – 13) = 0
x = 12, 13
Hence, if the marks in Maths are 12, then marks in English will be 30 – 12 = 18
and, the marks in Maths are 13, then marks in English will be 30 – 13 = 17.
问题6.矩形场的对角线比短边大60米。如果较长的一面比较短的一面多30米,请找到视野的两边。
解决方案:
Let’s take,
Breadth = x
Length = x+30
Diagonal = x+60

Diagonal = √(Length2 + Breadth2)
According to the given condition,
√((x+30)2 + (x)2) = x+60
Squaring both sides,
x2 + (x + 30)2 = (x + 60)2
x2 + x2 + 900 + 60x = x2 + 3600 + 120x
x2 – 60x – 2700 = 0
x2 – 90x + 30x – 2700 = 0
x(x – 90) + 30(x -90) = 0
(x – 90)(x + 30) = 0
x = 90, -30
As, side of the field cannot be negative.
Hence, the length of the shorter side will be 90 m.
and, the length of the larger side will be (90 + 30) m = 120 m.
问题7.两个数字的平方差是180。较小数字的平方是较大数字的8倍。找到两个数字。
解决方案:
Let’s take,
The larger number = x
and, smaller number = y
According to the given condition,
x2 – y2 = 180 and y2 = 8x (It means x has to be positive, because it is obtained by squaring a number)
x2 – 8x = 180
x2 – 8x – 180 = 0
x2 – 18x + 10x – 180 = 0
x(x – 18) +10(x – 18) = 0
(x – 18)(x + 10) = 0
x = 18, -10
As x cannot be negative,
Hence, the larger number will be 18.
x = 18
So, As y2 = 8x
= 8 × 18
= 144
y = ±√144 = ±12
So, Smaller number = ±12
Hence, the numbers are 18 and 12 or 18 and -12.
问题8.火车以匀速行驶360公里。如果速度提高了5 km / h,则相同的旅程将少花1个小时。找到火车的速度。
解决方案:
Let’s take
The speed of the train = x km/hr.
As, Speed =![]()
Time taken to cover 360 km =![]() hr.
hr.
As per the question given,
(x + 5)(![]() – 1) = 360
– 1) = 360
(x + 5)(![]() ) = 360
) = 360
(x + 5)(360 – x) = 360x
x2 + 5x -1800 = 0
x2 + 45x – 40x + 1800 = 0
x(x + 45) -40(x + 45) = 0
(x + 45)(x – 40) = 0
x = 40, -45
As we know, the value of speed cannot be negative.
Hence, the speed of train is 40 km/h.
问题9.两个水龙头可以一起装满9个水箱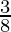 小时。较大直径的水龙头要比较小的水龙头少花10个小时,以便分别填充水箱。找出每个水龙头可以分别填充水箱的时间。
小时。较大直径的水龙头要比较小的水龙头少花10个小时,以便分别填充水箱。找出每个水龙头可以分别填充水箱的时间。
解决方案:
Let’s take
The time taken by the smaller pipe to fill the tank = x hr.
Time taken by the larger pipe = (x – 10) hr
Part of tank filled by smaller pipe in 1 hour =![]()
Part of tank filled by larger pipe in 1 hour =![]()
According to the given condition,
9![]() hrs taken to fill with both the pipe.
hrs taken to fill with both the pipe.
So,
![]()
![]()
![]()
75(2x – 10) = 8x2 – 80x
150x – 750 = 8x2 – 80x
8x2 – 230x +750 = 0
8x2 – 200x – 30x + 750 = 0
8x(x – 25) -30(x – 25) = 0
(x – 25)(8x -30) = 0
x = 25,![]()
Time taken by the smaller pipe cannot be![]() hours, as the time taken by the larger pipe will become negative.
hours, as the time taken by the larger pipe will become negative.
Hence, time taken by the smaller pipe = 25hours
and, by the larger pipe =15 hours
问题10:在迈索尔和班加罗尔之间行驶132公里(不考虑中间站的停留时间),快车比旅客列车少花1个小时。如果快车的平均速度比旅客列车的平均速度高11 km / h,请找到两列火车的平均速度。
解决方案:
Let’s take
The average speed of passenger train = x km/h.
Average speed of express train = (x + 11) km/h
According to the given condition,
![]() = 1
= 1
![]() = 1
= 1
![]() = 1
= 1
132 × 11 = x(x + 11)
x2 + 11x – 1452 = 0
x2 + 44x -33x -1452 = 0
x(x + 44) -33(x + 44) = 0
(x + 44)(x – 33) = 0
x = – 44, 33
As we know, Speed cannot be negative.
Hence, the speed of the passenger train will be 33 km/h
and, the speed of the express train will be 33 + 11 = 44 km/h.
问题11:两个正方形的面积之和为468 m 2 。如果它们的周长差为24 m,请找到两个正方形的边。
解决方案:
Let the sides of the two squares be x and y meter.
Perimeter = 4x and 4y respectively
Area = x2 and y2 respectively.
According to the given condition,
4x – 4y = 24
x – y = 6
x = y + 6 ………………….(I)
and,
x2 + y2 = 468
(6 + y)2 + y2 = 468 (From (I))
36 + y2 + 12y + y2 = 468
2y2 + 12y + 432 = 0
y2 + 6y – 216 = 0
y2 + 18y – 12y – 216 = 0
y(y +18) -12(y + 18) = 0
(y + 18)(y – 12) = 0
y = -18, 12
As we know, the side of a square cannot be negative.
Hence, the sides of the squares are 12 m
and, (12 + 6) m = 18 m.