10类NCERT解决方案-第6章三角形-练习6.2

Theorem 6.1 :

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Theorem 6.2 :

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

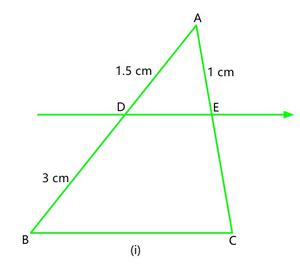
问题1.在图(i)和(ii)中，DE ||公元前。在(i)中找到EC，在(ii)中找到AD。

解决方案：

(i) Here, In △ ABC,

DE || BC

So, according to Theorem 6.1

$\frac{AD}{DB} = \frac{AE}{EC}$

⇒$\frac{1.5}{3} = \frac{1}{EC}$

⇒EC =$\frac{3×1}{1.5}$

EC = 2 cm

Hence, EC = 2 cm.

(ii) Here, In △ ABC,

So, according to Theorem 6.1 , if DE || BC

$\frac{AD}{DB} = \frac{AE}{EC}$

⇒$\frac{AD}{7.2} = \frac{1.8}{5.4}$

⇒AD =$\frac{1.8×7.2}{5.4}$

AD = 2.4 cm

Hence, AD = 2.4 cm.

问题2. E和F分别是∆ PQR边PQ和PR上的点。对于以下每种情况，请说明EF ||是否为EF ||。 QR：

(i)PE = 3.9厘米，EQ = 3厘米，PF = 3.6厘米，FR = 2.4厘米

解决方案：

According to the Theorem 6.2,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

So, lets check the ratios

Here, In △ PQR,

$\frac{PE}{EQ} = \frac{3.9}{3}$= 1.3 ………………………(i)

$\frac{PF}{FR} = \frac{3.6}{2.4}$= 1.5 ………………………(ii)

As,$\frac{PE}{EQ} ≠ \frac{PF}{FR}$

Hence, EF is not parallel to QR.

(ii)PE = 4厘米，QE = 4.5厘米，PF = 8厘米，RF = 9厘米

解决方案：

According to the Theorem 6.2,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

So, lets check the ratios

Here, In △ PQR,

$\frac{PE}{EQ} = \frac{4}{4.5} = \frac{8}{9}$………………………(i)

$\frac{PF}{FR} = \frac{8}{9}$………………………(ii)

As,$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

(iii)PQ = 1.28厘米，PR = 2.56厘米，PE = 0.18厘米，PF = 0.36厘米

解决方案：

EQ = PQ – PE = 1.28 – 0.18 = 1.1

and, FR = PR – PF = 2.56 – 0.36 = 2.2

According to the Theorem 6.2,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

So, lets check the ratios

Here, In △ PQR,

$\frac{PE}{EQ} = \frac{0.18}{1.1} = \frac{9}{55}$………………………(i)

$\frac{PF}{FR} = \frac{0.36}{2.2} = \frac{9}{55}$………………………(ii)

As,$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

问题3.在图中，如果LM || CB和LN || CD，证明

$\frac{AM}{AB} = \frac{AN}{AD}$

解决方案：

Here, In △ ABC,

According to Theorem 6.1, if LM || CB

then,$\frac{AM}{AB} = \frac{AL}{AC}$…………………………….(I)

and, In △ ADC,

According to Theorem 6.1, if LN || CD

then,$\frac{AN}{AD} = \frac{AL}{AC}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{AM}{AB} = \frac{AN}{AD}$

Hence Proved !!

问题4.在图中，DE || AC和DF || AE。证明

$\frac{BF}{FE} = \frac{BE}{EC}$

解决方案：

Here, In △ ABC,

According to Theorem 6.1, if DE || AC

then,$\frac{BD}{DA} = \frac{BE}{EC}$…………………………….(I)

and, In △ ABE,

According to Theorem 6.1, if DF || AE

then,$\frac{BD}{DA} = \frac{BF}{FE}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{BF}{FE} = \frac{BE}{EC}$

Hence Proved !!

问题5.在图中，DE || OQ和DF ||或者。显示EF || QR

解决方案：

Here, In △ POQ,

According to Theorem 6.1, if DE || OQ

then,$\frac{PE}{EQ} = \frac{PD}{DO}$…………………………….(I)

and, In △ POR,

According to Theorem 6.1, if DF || OR

then,$\frac{PD}{DO} = \frac{PF}{FR}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{PE}{EQ} = \frac{PF}{FR}$………………………………(III)

According to Therem 6.2 and eqn. (III)

EF || QR, in △ PQR

Hence Proved !!

问题6。在图中，A，B和C分别是OP，OQ和OR上的点，因此AB || PQ和AC ||公关显示BC || QR

解决方案：

Here, In △ POQ,

According to Theorem 6.1, if AB || PQ

then,$\frac{OA}{AP} = \frac{OB}{BQ}$…………………………….(I)

and, In △ POR,

According to Theorem 6.1, if AC || PR

then,$\frac{OA}{AP} = \frac{OC}{CR}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{OB}{BQ} = \frac{OC}{CR}$………………………………(III)

According to Therem 6.2 and eqn. (III)

BC || QR, in △ OQR

Hence Proved !!

问题7.使用定理6.1，证明通过平行于另一边的三角形的一侧的中点画出的线将第三侧平分。

解决方案：

Given, in ΔABC, D is the midpoint of AB such that AD=DB.

A line parallel to BC intersects AC at E

So, DE || BC.

We have to prove that E is the mid point of AC.

As, AD=DB

⇒$\frac{AD}{DB}$= 1 …………………………. (I)

Here, In △ ABC,

According to Theorem 6.1, if DE || BC

then,$\frac{AD}{DB} = \frac{AE}{EC}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{AD}{DB} = \frac{AE}{EC}$= 1

$\frac{AE}{EC}$= 1

AE = EC

E is the midpoint of AC.

Hence proved !!

问题8.使用定理6.2，证明连接三角形任意两个边的中点的线与第三边平行。

解决方案：

Given, in ΔABC, D and E are the mid points of AB and AC respectively

AD=BD and AE=EC.

We have to prove that: DE || BC.

As, AD=DB

⇒$\frac{AD}{DB}$= 1 …………………………. (I)

and, AE=EC

⇒$\frac{AE}{EC}$= 1 …………………………. (II)

From (I) and (II), we conclude that

$\frac{AD}{DB} = \frac{AE}{EC}$= 1 ……………….(III)

According to Therem 6.2 and eqn. (III)

DE || BC, in △ ABC

Hence Proved !!

问题9. ABCD是一个梯形，其中AB || DC及其对角线在点O处相交。

$\frac{AO}{BO} = \frac{CO}{DO}$

解决方案：

From the point O, draw a line EO touching AD at E, in such a way that,

EO || DC || AB

Here, In △ ADB,

According to Theorem 6.1, if AB || EO

then,$\frac{AE}{ED} = \frac{OB}{OD}$…………………………….(I)

and, In △ ADC,

According to Theorem 6.1, if AC || PR

then,$\frac{AE}{ED} = \frac{AO}{OC}$…………………………….(II)

From (I) and (II), we conclude that

$\frac{AO}{OC} = \frac{OB}{OD}$

After rearranging, we get

$\frac{AO}{OB} = \frac{OC}{OD}$

Hence Proved !!

问题10.四边形ABCD的对角线在点O处相交，使得

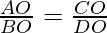$\frac{AO}{BO} = \frac{CO}{DO}$ 。证明ABCD是梯形。

解决方案：

From the point O, draw a line EO touching AD at E, in such a way that,

EO || DC || AB

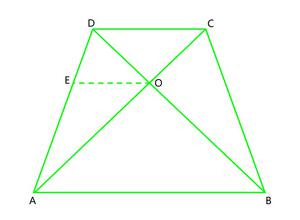
Here, In △ ADB,

According to Theorem 6.1, if AB || EO

then,$\frac{AE}{ED} = \frac{OB}{OD}$…………………………….(I)

$\frac{AO}{OB} = \frac{OC}{OD}$(Given)

$\frac{AO}{OC} = \frac{OB}{OD}$(After rearranging) ………………………………..(II)

From (I) and (II), we conclude that

$\frac{AE}{ED} = \frac{AO}{OC}$………………………………..(III)

According to Therem 6.2 and eqn. (III)

EO || DC and also EO || AB

⇒ AB || DC.

Hence, quadrilateral ABCD is a trapezium with AB || CD.