NCERT Theorem 1.5 : Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form, ![]() where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
NCERT Theorem 1.6 : Let x = ![]() be a rational number, such that the prime factorization of q is of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
be a rational number, such that the prime factorization of q is of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
问题1.在没有实际执行长除法的情况下,请说明以下有理数将具有终止的十进制扩展数还是具有非终止的重复十进制扩展数:
(一世) 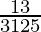
(ii) 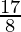
(iii) 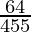
(iv) 
(v) 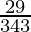
(六) 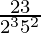
(vii) 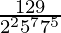
(viii) 
(ix) 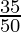
(X) 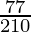
解决方案:
(i) ![]()
By doing prime factorization of denominator, we get
3125 = 5×5×5 = 53
As denominator is in the form 2n5m only where n=0 and m=3.
According to Theorem 1.6,
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(ii) ![]()
By doing prime factorization of denominator, we get
8 = 2×2×2 = 23
As denominator is in the form 2n5m only where n=3 and m=0.
According to Theorem 1.6,
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(iii) ![]()
By doing prime factorization of denominator, we get
455 = 5×7×13
As denominator is not in the form 2n5m only.
According to contradiction of Theorem 1.6,
![]() will have a non-terminating decimal expansion.
will have a non-terminating decimal expansion.
(iv) ![]()
By doing prime factorization of denominator, we get
1600 = 2×2×2×2×2×2×5×5 = 2652
As denominator is in the form 2n5m only where n=6 and m=2.
According to Theorem 1.6, 1
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(v) ![]()
By doing prime factorization of denominator, we get
343 = 7×7×7 = 73
As denominator is not in the form 2n5m only.
According to contradiction of Theorem 1.6,
![]() will have a non-terminating decimal expansion.
will have a non-terminating decimal expansion.
(vi) ![]()
Prime factorization of denominator, we have
= 2352
As denominator is in the form 2n5m only where n=3 and m=2.
According to Theorem 1.6,
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(vii) ![]()
Prime factorization of denominator, we have
= 225775
As denominator is not in the form 2n5m only.
According to contradiction of Theorem 1.6,
![]() will have a non-terminating decimal expansion.
will have a non-terminating decimal expansion.
(viii) ![]()
![]()
by doing prime factorization of denominator, we get
5 = 51
As denominator is in the form 2n5m only where n=0 and m=1.
According to Theorem 1.6,
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(ix) ![]()
by doing prime factorization of denominator, we get
50= 2×5×5 = 2152
As denominator is in the form 2n5m where n=1 and m=2.
According to Theorem 1.6,
![]() will have a terminating decimal expansion.
will have a terminating decimal expansion.
(x) ![]()
by doing prime factorization of denominator, we get
210 = 2×3×5×7
As denominator is not in the form 2n5m only.
According to contradiction of Theorem 1.6,
![]() will have a non-terminating decimal expansion.
will have a non-terminating decimal expansion.
问题2。写下上面问题1中那些有终止十进制扩展的有理数的十进制扩展。
(一世) 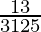
(ii) 
(iv) 
(六) 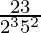
(viii) 
(ix) 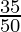
解决方案:
(i) ![]()
= 0.00416
(ii) ![]()
= 2.125
(iv) ![]()
= 0.009375
(vi) ![]()
= 0.0115
(viii) ![]()
= 0.4
(ix) ![]()
= 0.7
问题3.以下实数具有十进制扩展名,如下所示。在每种情况下,请确定它们是否合理。如果它们是理性的,并且形式如此, 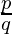 关于q的素数,您能说什么?
关于q的素数,您能说什么?
(i)43.123456789
(ii)0.120120012000120000。 。 。
(iii)43.123456789
解决方案:
(i) 43.123456789
As this is a rational number whose decimal expansion terminates. Then it can be expressed in the form, ![]() where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
= 43123456789 / 109
= 43123456789 / 29 × 59
(ii) 0.120120012000120000…………..
As given decimal number expansion is non-terminating and non-repeating, then it is not a rational number. Then it can’t be expressed in the form, ![]() where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
where p and q are coprime, and the prime factorization of q is of the form 2n5m, where n, m are non-negative integers.
(iii) 43.![]() [Tex] [/Tex]
[Tex] [/Tex]
As given decimal number expansion is non-terminating and repeating, then it is a rational number. Then it can be expressed in the form, ![]() where p and q are coprime, but the prime factorization of q is not in the form of 2n5m only, where n, m are non-negative integers
where p and q are coprime, but the prime factorization of q is not in the form of 2n5m only, where n, m are non-negative integers