第11类RD Sharma解决方案–第13章复数–练习13.4

问题1.找到以下复数的模数和自变量，并以极形式表示它们中的每一个：

(i)1 +我

(ii)√3+ i

(iii)1 –我

(iv)(1 – i)/(1 + i)

(v)1 /(1 + i)

(vi)(1 + 2i)/(1 – 3i)

(vii)罪120 ^o –我cos 120 ^o

(viii) –16 /(1 +i√3)

The polar form of a complex number Z = x + iy is given by Z = |Z| (cos θ + i sin θ) where,

Modulus of complex number, |Z| = √(x² + y²)

Argument of complex number, θ = arg (Z) = tan^–1 (y/x)

(i)1 +我

解决方案：

We are given, Z = 1 + i, so x = 1 and y = 1.

|Z| = √(1² + 1²) = √2

θ = tan^-1 (1/1) = tan^-1 1

As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.

So, θ = π/4 and Z = √2 (cos (π/4) + i sin (π/4)) 

Therefore, the polar form of (1 + i) is √2 (cos (π/4) + i sin (π/4)).

(ii)√3+ i

解决方案：

We are given, Z = √3 + i, so x = √3 and y = 1.

|Z| = √((√3)² + 1²) = 2

θ = tan^-1 (1/√3) 

As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.

So, θ = π/6 and Z = 2 (cos (π/6) + i sin (π/6))

Therefore, the polar form of (√3 + i) is √2 (cos (π/6) + i sin (π/6)).

(iii)1 –我

解决方案：

We are given, Z = 1 – i, so x = 1 and y = –1.

|Z| = √(1)² + (–1)²) = √2

θ = tan^-1 (1/1) = tan^-1 1  

As x > 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.

So, θ = – π/4 and,

Z = √2 (cos (–π/4) + i sin (–π/4))

= √2 (cos (π/4) – i sin (π/4))

Therefore, the polar form of (1 – i) is √2 (cos (π/4) – i sin (π/4)).

(iv)(1 – i)/(1 + i)

解决方案：

We are given, Z = (1 – i)/(1 + i).

Multiplying and dividing by (1 – i), we get,

Z = $\frac{1 - i}{1 + i}×\frac{1 - i}{1 - i}$

= $\frac{1+i^2-2i}{1-i^2}$

= $\frac{1+(-1)-2i}{1-(-1)}$

= $\frac{-2i}{2}$

= 0 – i

So x = 0, y = –1 and |Z| = √(0² + (–1)²) = 1

θ =  tan^-1 (1/0)

As x ≥ 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.

So, θ = –π/2 and,

Z = 1 (cos (–π/2) + i sin (–π/2))

= cos (π/2) – i sin (π/2)

Therefore, the polar form of (1 – i)/(1 + i) is cos (π/2) – i sin (π/2).

(v)1 /(1 + i)

解决方案：

We are given, Z = (1 – i)/(1 + i).

Multiplying and dividing by (1 – i), we get,

Z = $\frac{1}{1 + i}×\frac{1 - i}{1 - i}$

= $\frac{1-i}{1-i^2}$

= $\frac{1-i}{1-(-1)}$

= $\frac{1-i}{2}$

= 1/2 – i/2

So x = 1/2, y = –1/2 and |Z| = √((1/2)² + (–1/2)²) = √(2/4) = 1/√2

θ =  tan^-1 ((1/2)/(1/2)) = tan^–1 1

As x > 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.

So, θ = –π/4 and,

Z = 1/√2 (cos (-π/4) + i sin (-π/4))

= 1/√2 (cos (π/4) – i sin (π/4))

Therefore, the polar form of 1/(1 + i) is 1/√2 (cos (π/4) – i sin (π/4)).

(vi)(1 + 2i)/(1 – 3i)

解决方案：

We are given, Z = (1 + 2i)/(1 – 3i).

Multiplying and dividing by (1 + 3i), we get,

Z = $\frac{1+2i}{1-3i}×\frac{1+3i}{1+3i}$

= $\frac{1+3i+2i+6i^2}{1-9i^2}$

= $\frac{1+5i+6(-1)}{1-9(-1)}$

= $\frac{-5+5i}{10}$

= –1/2 + i/2

So x = –1/2, y = 1/2 and |Z| = √((–1/2)² + (1/2)²) = √(2/4) = 1/√2

θ =  tan-1 ((1/2)/(1/2)) = tan^–1 1

As  x < 0 and y > 0, Z lies in 2nd quadrant and the value of θ is π/2 ≤ θ ≤ π.

So, θ = 3π/4 and Z = 1/√2 (cos (3π/4) + i sin (3π/4))

Therefore, the polar form of (1 + 2i)/(1 – 3i) is 1/√2 (cos (3π/4) + i sin (3π/4)).

(vii)罪120 ^o –我cos 120 ^o

解决方案：

We are given, Z = sin 120^o – i cos 120^o

= √3/2 – i (–1/2)

= √3/2 + i (1/2)

So x = √3/2, y = 1/2 and |Z| = √((√3/2)² + (1/2)²) = √(3/4 + 1/4) = 1

θ = tan^-1 ((1/2)/(√3/2)) = tan^-1 (1/√3)

As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.

So, θ = π/6 and Z = 1 (cos (π/6) + i sin (π/6))

Therefore, the polar form of √3/2 + i (1/2) is 1 (cos (π/6) + i sin (π/6)).

(viii)-16 /(1 +i√3)

We are given, Z = –16/(1 + i√3).

Multiplying and dividing by (1 – i√3), we get,

Z = $\frac{-16}{1+\sqrt{3}i}×\frac{1-\sqrt{3}i}{1-\sqrt{3}i}$

= $\frac{-16+16\sqrt{3}i}{1-3i^2}$

= $\frac{-16+16\sqrt{3}i}{4}$ 

= –4 + 4√3 i

So x = –4, y = 4/√3 and |Z| = √((–4)² + (4√3)²) = √(16 + 48) = 8

θ = tan^-1 (4√3/4) = tan^-1 (√3)

As x < 0 and y > 0, Z lies in 2nd quadrant and the value of θ is π/2 ≤ θ ≤ π.

So, θ = 2π/3 and Z = 8 (cos (2π/3) + i sin (2π/3))

Therefore, the polar form of -16 / (1 + i√3) is 8 (cos (2π/3) + i sin (2π/3)).

问题2.以极形式写(i ²⁵ ) ^3。

解决方案：

We are given, 

 Z = (i²⁵)³

= i⁷⁵

= (i²)³⁷. i

= (–1)³⁷. i

= – i

= 0 – i

So x = 0, y = –1 and,

|Z| = √(x² + y²)

= √(0² + (–1)²)

= 1

θ = tan^–1 (|y| / |x|)

= tan^–1 (1 / 0)

Since x ≥ 0 and y < 0, Z lies in 4th quadrant and the value of θ is π/2 ≤ θ ≤ 0. So, θ = –π/2.

Z = 1 (cos (–π/2) + i sin (–π/2))

= 1 (cos (π/2) – i sin (π/2))

Therefore, the polar form of (i²⁵)³ is 1 (cos (π/2) – i sin (π/2)).

问题3.以r(cosθ + i sinθ )的形式表示以下复数：

(i)1 +我tanα

(ii)棕褐色α– i

解决方案：

(i) 1 + i tan α

We are given 1 + i tan α, so x =1 and y = tan α. 

We also know that tan α is a periodic function with period π. 

So α is lying in the interval [0, π/2) ∪ (π/2, π].

Case 1: If α ∈ [0, π/2)

|Z| = r = √(1² + tan² α)

= √( sec² α)

= sec α

θ = tan^-1 (tan α/1)

= tan^-1 (tan α)

= α 

So, Z = sec α (cos α + i sin α)

Therefore, polar form is sec α (cos α + i sin α).

Case 2: α ∈ (π/2, π]

|Z| = r = √(1² + tan² α)

= √( sec² α)

= – sec α

θ = tan^-1 (tan α/1)

= tan^-1 (tan α)

= –π + α

So, Z = –sec α (cos (α – π) + i sin (α – π))

Therefore, polar form is –sec α (cos (α – π) + i sin (α – π)).

(ii) tan α – i

We are given tan α – i, so x =tan α and y = –1.

We also know that tan α is a periodic function with period π.

So α is lying in the interval [0, π/2) ∪ (π/2, π].

Case 1: If α ∈ [0, π/2)

|Z| = r = √(tan² α + 1)

= √( sec² α)

= sec α

θ = tan^-1 (1/tan α)

= tan^-1 (cot α)

= α – π/2

So, Z = sec α (cos (α – π/2) + i sin (α – π/2))

Therefore, polar form is sec α (cos (α – π/2) + i sin (α – π/2)).

Case 2: α ∈ (π/2, π]

|Z| = r = √(tan² α + 1)

= √( sec² α)

= – sec α

θ = tan^-1 (1/tan α)

= tan^-1 (cot α)

= π/2 + α

So, Z =  –sec α (cos (π/2 + α) + i sin (π/2 + α))

Therefore, polar form is –sec α (cos (π/2 + α) + i sin (π/2 + α)).

问题4.如果z ₁和z ₂是两个复数，则| z ₁ | = | z ₂ |并且arg(z ₁ )+ arg(z ₂ )=π，然后证明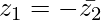$z_1 = -\bar{z_2}$ 。

解决方案：

We are given |z₁| = |z₂| and arg (z₁) + arg (z₂) = π. Suppose arg (z₁) = θ, then arg (z₂) = π – θ.

We know z = |z| (cos θ + i sin θ)

z₂ = |z₂| (cos (π – θ) + i sin (π – θ))

= |z₂| (–cos θ + i sin θ)

= – |z₂| (cos θ – i sin θ)

The conjugate of z₂, $\bar{z_2}$ = – |z₂| (cos θ + i sin θ)

Now L.H.S. = z₁ = |z₁| (cos θ + i sin θ)

= |z₂| (cos θ + i sin θ)

= – [– |z₂| (cos θ + i sin θ)]

= $-\bar{z_2}$

= R.H.S.

Hence proved.

问题5.如果z ₁ ，z ₂和z ₃ ，z ₄是两对共轭复数，则证明arg(z ₁ / z ₄ )+ arg(z ₂ / z ₃ )= 0

解决方案：

We are given,

$z_1=\bar{z_2}$

$z_3=\bar{z_4}$

L.H.S. = arg (z₁/z₄) + arg (z₂/z₃)

= arg (z₁) − arg (z₄) + arg (z₂) − arg (z₃)

= [arg (z₁) + arg (z₂)] − [arg (z₃) + arg (z₄)] 

= $[arg(z_2)+arg(\bar{z_2})]−[arg(z_4)+arg(\bar{z_4})]$

= 0 − 0

= 0 

= R.H.S

Hence proved.

问题6.以极性形式表达sinπ / 5 + i(1 – cosπ / 5)。

解决方案：

We are given,

Z = sin π/5 + i (1 – cos π/5)

= 2 sin π/10 cos π/10 + i (2 sin² π/10)

= 2 sin π/10 (cos π/10 + i sin π/10)

We know the polar form is given by r (cos θ + i sin θ).

Therefore, the polar form of the given expression is 2 sin π/10 (cos π/10 + i sin π/10).