第6章线性不等式–练习6.1 |套装1
问题13. 2(2x + 3)– 10 <6(x – 2)
解决方案:
Given, 2(2x + 3) – 10 < 6 (x – 2)
By multiplying we get
4x + 6 – 10 < 6x – 12
On simplifying we get
4x – 4 < 6x – 12
– 4 + 12 < 6x – 4x
8 < 2x
4 < x
Thus, the solutions of the given equation are defined by all the real numbers greater than or equal to 4.
Hence, the required solution set is [4, ∞)
问题14. 37 –(3x + 5) ≥9x – 8(x – 3)
解决方案:
Given that, 37 – (3x + 5) ≥ 9x – 8 (x – 3)
On simplifying we get
37 – 3x – 5 ≥ 9x – 8x + 24
32 – 3x ≥ x + 24
On rearranging
32 – 24 ≥ x + 3x
8 ≥ 4x
2 ≥ x
All the real numbers of x which are less than or equal to 2 are the solutions of the given equation
Hence, (-∞, 2] will be the solution for the given equation
问题15. x / 4 <(5x-2)/ 3-(7x-3)/ 5
解决方案:
Given, x/4<(5x-2)/3-(7x-3)/5
Taking 15 as the lcm on the right side
x/4<(5(5x-2)-3(7x-3))/15
Further, simplifying we get,
x/4<((25x-10)-(21x-9))/15
Multiplying 15 at both the sides
15x/4<25x-10-21x+9
15x/4<4x-1
Multiplying by 4 we get
15x < 4 (4x – 1)
15x < 16x – 4
4 < x
All the real numbers of x which are greater than 4 are the solutions of the given equation
Hence, (4, ∞) will be the solution for the given equation
问题16.(2x-1)/ 3> =(3x-2)/ 4-(2-x)/ 5
解决方案:
Let us simplify the inequation
(2x-1)/3>=(5(3x-2)-4(2-x))/20
(2x-1)/3>=((15x-10)-(8-4x))/20
(2x-1)/3>=(15x-10-8+4x)/20
(2x-1)/3>=(19x-18)/20
Now cross multiplying at both the sides we get
20 (2x – 1) ≥ 3 (19x – 18)
40x – 20 ≥ 57x – 54
– 20 + 54 ≥57x – 40x
34 ≥ 17x
2 ≥ x
∴ All the real numbers of x which are less than or equal to 2 are the solutions of the given equation
Hence, (-∞, 2] will be the solution for the given equation
解决练习17至20中的不等式,并在每种情况下在数字线上显示解决方案的图形。
问题17. 3x – 2 <2x + 1
解决方案:
Given, 3x – 2 < 2x + 1Solving the given inequality, we get
3x – 2 < 2x + 1
3x – 2x < 1 + 2
x < 3
Now, the graphical representation of the solution is as follows:

问题18。5x– 3≥3x – 5
解决方案:
We have,5x – 3 ≥ 3x – 5
Solving the given inequality, we get
5x – 3 ≥ 3x – 5
On rearranging we get
5x – 3x ≥ -5 + 3
On simplifying 2x ≥ -2
Now divide by 2 on both sides we get
x ≥ -1
The graphical representation of the solution is as follows:

问题19. 3(1 – x)<2(x + 4)
解决方案:
Given,3 (1 – x) < 2 (x + 4)
Solving the given inequality, we get
3 (1 – x) < 2 (x + 4)
Multiplying we get 3 – 3x < 2x + 8
On rearranging we get
3 – 8 < 2x + 3x
– 5 < 5x
Now by dividing 5 on both sides we get
-5/5 < 5x/5
– 1 < x
Now, the graphical representation of the solution is as follows:
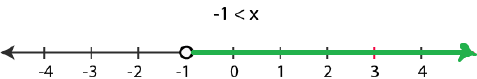
问题20. x / 2> =(5x-2)/ 3-(7x-3)/ 5
解决方案:
Let us solve the right side of the inequation
x/2>=(5(5x-2)-(7x-3)3)/15
x/2>=(25x-10-21x+9)/15
x/2>=(4x+1)/15
15x ≥ 2 (4x – 1)
15x ≥ 8x -2
15x -8x ≥ 8x -2 -8x
7x ≥ -2
x ≥ -2/7
Now, the graphical representation of the solution is as follows:

问题21. Ravi在前两个单元测试中分别获得了70分和75分。找到他在第三次考试中应获得的最低分数,以使平均分数至少达到60分。
解决方案:
Let us assume that the marks obtained by Ravi in his third unit test be x,
According to question,
the entire students should have an average of at least 60 marks i.e,
(70 + 75 + x)/3 ≥ 60
145 + x ≥ 180
x ≥ 180 – 145
x ≥ 35
Thus, all the students must obtain 35 marks in order to have an average of at least 60 marks
问题22.要获得一门课程的“ A”级成绩,必须在五门考试中平均取得90分以上(每门100分)。如果Sunita在前四次考试中的分数分别为87、92、94和95,请找到Sunita在第五次考试中必须获得的最低分数才能在课程中获得“ A”级。
解决方案:
Let us assume Sunita scored x marks in her 5th examination
Now, according to the question
In order to receive A grade in the course she must have to obtain average 90 marks or more in her five examinations that is,
(87 + 92 + 94 + 95 + x)/5 ≥ 90
(368 + x)/5 ≥ 90
368 + x ≥ 450
x ≥ 450 – 368
x ≥ 82
Thus, she must have to obtain 82 or more marks in her fifth examination
问题23.查找所有均小于10且其总和大于11的所有连续的奇异正整数对。
解决方案:
Let us assume x be the smaller of the two consecutive odd positive integers
Let other integer = x + 2
It is also given in the question that,
both the integers are smaller than 10 that is,
x + 2 < 10
x< 8 … (a)
Also, it is given in the question that sum off two integers is more than 11
∴ x + (x + 2) > 11
2x + 2 > 11
x > 9/2
x > 4.5 … (b)
Thus, from (a) and (b) we have x is an odd integer and it can take values 5 and 7
Hence, possible pairs are (5, 7) and (7, 9)
问题24.查找所有成对的连续偶数正整数,这两个整数均大于5且其总和小于23。
解决方案:
Let us assume x be the smaller of the two consecutive even positive integers
Let other integer= x + 2
It is also given in the question that, both the integers are larger than 5∴
x > 5 ….(a)
Also, it is given in the question that the sum of two integers is less than 23.
∴ x + (x + 2) < 23
2x + 2 < 23
x < 21/2
x < 10.5 …. (b)
Thus, from (a and (b) we have x is an even number and it can take values 6, 8 and 10
Thus, the possible pairs are (6, 8), (8, 10) and (10, 12).
问题25.三角形的最长边是最短边的3倍,而第三边比最长边短2厘米。如果三角形的周长至少为61厘米,则找到最短边的最小长度。
解决方案:
Let us assume that the length of the shortest side of the triangle be x cm
According to the question,
length of the longest side = 3x cm
And, length of third side = (3x – 2) cm
As, the least perimeter of the triangle = 61 cm
Thus, x + 3x + (3x – 2) cm ≥ 61 cm
7x – 2 ≥ 61
7x ≥ 63
Now let us divide by 7 we get=
7x/7 ≥ 63/7=
x ≥ 9
Hence, the minimum length of the shortest side will be 9 cm
问题26.一个人想要从一块91厘米长的木板上切下三个长度。第二个长度应比最短的长度长3厘米,第三个长度应是最短的长度的两倍。如果第三块比第二块至少长5厘米,那么最短板的可能长度是多少?
解决方案:
Let us assume that the length of the shortest piece be x cm
∴ According to the question,
Length of the second piece = (x + 3) cm
And, length of third piece = 2x cm
As all the three lengths are to be cut from a single piece of board having a length of 91 cm
x + (x + 3) + 2x ≤ 91 cm
4x + 3 ≤ 91
4x ≤ 88
4x/4 ≤ 88/4
x ≤ 22 … (i)
Also, it is given in the question that, the third piece is at least 5 cm longer than the second piece
2x ≥ (x+3) + 5
2x ≥ x + 8
x ≥ 8 … (ii)
Thus, from equation (i) and (ii) we have:
8 ≤ x ≤ 22
Hence, it is clear that the length of the shortest board is greater than or equal to 8 cm and less than or equal to 22 cm