11类NCERT解决方案–第六章线性不等式–练习6.3

以图形方式解决以下不等式系统：

问题1：x≥3，y≥2

解决方案：

For equation 1:

Now draw a solid line x = 3 in the graph (because (x = 3) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
3	0
3	5

Consider x ≥ 3

Lets, select origin point (0, 0)

⇒ 0 ≥ 3

⇒ 0 ≥ 3 (this not is true)

Hence, Solution region of the given inequality is the line x ≥ 3. where, Origin is not included in the region

For equation 2:

Now draw a solid line y = 2 in the graph (because (y = 2) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	2
3	2

Consider y ≥ 2

Lets, select origin point (0, 0)

⇒ 0 ≥ 2

⇒ 0 ≥ 2 (this not is true)

Hence, Solution region of the given inequality is the line y ≥ 2. where, Origin is not included in the region

The graph will be as follows for Equation 1 and 2:

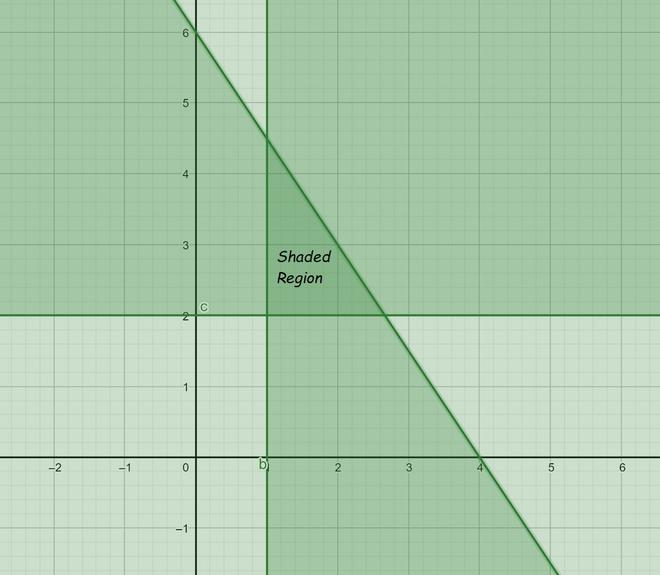
问题2：3x + 2y≤12，x≥1，y≥2

解决方案：

For equation 1:

Now draw a solid line 3x + 2y = 12 in the graph (because (3x + 2y = 12) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	6
4	0

Consider 3x + 2y ≤ 12

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 12

⇒ 0 + 0 ≤ 12 (this is true)

Hence, Solution region of the given inequality is the line 3x + 2y ≤ 12. where, Origin is included in the region

For equation 2:

Now draw a solid line x = 1 in the graph (because (x = 1) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	0
1	5

Consider x ≥ 1

Lets, select origin point (0, 0)

⇒ 0 ≥ 1

⇒ 0 ≥ 1 (this not is true)

Hence, Solution region of the given inequality is the line x ≥ 1. where, Origin is not included in the region

For equation 3:

Now draw a solid line y = 2 in the graph (because (y = 2) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	2
5	2

Consider y ≥ 2

Lets, select origin point (0, 0)

⇒ 0 ≥ 2

⇒ 0 ≥ 2 (this not is true)

Hence, Solution region of the given inequality is the line y ≥ 2. where, Origin is not included in the region

The graph will be as follows for Equation 1, 2 and 3:

问题3：2x + y≥6，3x + 4y <12

解决方案：

For equation 1:

Now draw a solid line 2x + y = 6 in the graph (because (2x + y = 6) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	6
3	0

Consider 2x + y ≥ 6

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 6

⇒ 0 ≥ 6 (this is not true)

Hence, Solution region of the given inequality is the line 2x + y ≥ 6. where, Origin is not included in the region

For equation 2:

Now draw a dotted line 3x + 4y = 12 in the graph (because (3x + 4y = 12) is NOT the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	3
4	0

Consider 3x + 4y < 12

Lets, select origin point (0, 0)

⇒ 0 + 0 < 12

⇒ 0 < 12 (this is true)

Hence, Solution region of the given inequality is the line 3x + 4y < 12. where, Origin is included in the region.

The graph will be as follows for Equation 1 and 2:

问题4：x + y≥4，2x – y <0

解决方案：

For equation 1:

Now draw a solid line x + y = 4 in the graph (because (x + y = 4) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	4
4	0

Consider x + y ≥ 4

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 4

⇒ 0 ≥ 4 (this is not true)

Hence, Solution region of the given inequality is the line x + y ≥ 4. where, Origin is not included in the region

For equation 2:

Now draw a dotted line 2x – y = 0 in the graph (because (2x – y = 0) is NOT the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
1	2

Consider 2x – y < 0

Lets, select point (3, 0)

⇒ 6 – 0 < 0

⇒ 0 > 6 (this is not true)

Hence, Solution region of the given inequality is the line 2x – y < 0. where, the point (3,0) is included in the region.

The graph will be as follows for Equation 1 and 2:

问题5：2x – y> 1，x – 2y <– 1

解决方案：

For equation 1:

Now draw a dotted line 2x – y =1 in the graph (because (2x – y =1) is NOT the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	-1
1	1

Consider 2x – y >1

Lets, select origin point (0, 0)

⇒ 0 – 0 > 1

⇒ 0 > 1 (this is not true)

Hence, Solution region of the given inequality is the line 2x – y >1. where, Origin is not included in the region

For equation 2:

Now draw a dotted line x – 2y = – 1 in the graph (because (x – 2y = – 1) is NOT the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	1
-1	0

Consider x – 2y < – 1

Lets, select point (3, 0)

⇒ 0 – 0 < -1

⇒ 0 < -1 (this is not true)

Hence, Solution region of the given inequality is the line x – 2y < – 1. Origin is not included in the region

The graph will be as follows for Equation 1 and 2:

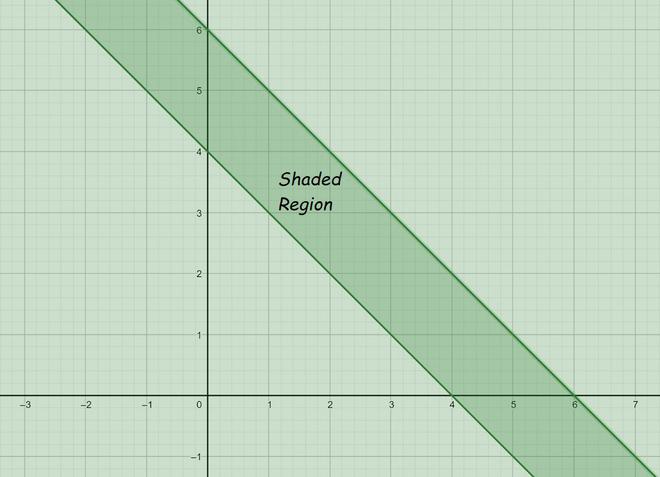
问题6：x + y≤6，x + y≥4

解决方案：

For equation 1:

Now draw a solid line x + y = 6 in the graph (because (x + y = 6) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	6
6	0

Consider x + y ≤ 6

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 6

⇒ 0 ≤ 6 (this is true)

Hence, Solution region of the given inequality is the line x + y ≤ 6. where, Origin is included in the region

For equation 2:

Now draw a solid line x + y = 4 in the graph (because (x + y = 4) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	4
4	0

Consider x + y ≥ 4

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 4

⇒ 0 ≥ 4 (this not is true)

Hence, Solution region of the given inequality is the line x + y ≥ 4. where, Origin is not included in the region

The graph will be as follows for Equation 1 and 2:

问题7：2x + y≥8，x + 2y≥10

解决方案：

For equation 1:

Now draw a solid line 2x + y = 8 in the graph (because (2x + y = 8) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	8
4	0

Consider 2x + y ≥ 8

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 8

⇒ 0 ≥ 8 (this is not true)

Hence, Solution region of the given inequality is the line 2x + y ≥ 8. where, Origin is not included in the region

For equation 2:

Now draw a solid line x + 2y = 10 in the graph (because (x + 2y = 10) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	5
10	0

Consider x + 2y ≥ 10

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 10

⇒ 0 ≥ 10 (this not is true)

Hence, Solution region of the given inequality is the line x + 2y ≥ 10. where, Origin is not included in the region

The graph will be as follows for Equation 1 and 2:

问题8：x + y≤9，y> x，x≥0

解决方案：

For equation 1:

Now draw a solid line x + y = 9 in the graph (because (x + y = 9) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	9
9	0

Consider x + y ≤ 9

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 9

⇒ 0 ≤ 9 (this is true)

Hence, Solution region of the given inequality is the line x + y ≤ 9. where, Origin is included in the region

For equation 2:

Now draw a dotted line y = x in the graph (because (y = x) is NOT the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	1
0	0

Consider y > x

Lets, select point (3, 0)

⇒ 0 > 3

⇒ 0 > 3 (this is not true)

Hence, Solution region of the given inequality is the line y > x. the point (3,0) is not included in the region.

For equation 3:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

The graph will be as follows for Equation 1, 2 and 3:

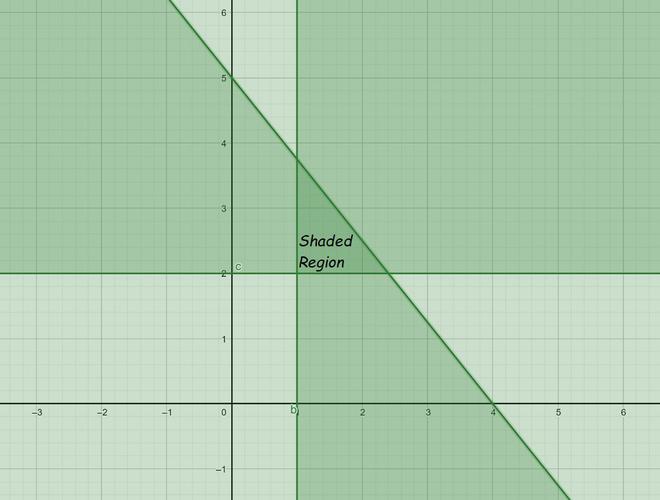
问题9：5x + 4y≤20，x≥1，y≥2

解决方案：

For equation 1:

Now draw a solid line 5x + 4y = 20 in the graph (because (5x + 4y = 20) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	5
4	0

Consider 5x + 4y ≤ 20

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 20

⇒ 0 ≤ 20 (this is true)

Hence, Solution region of the given inequality is the line 5x + 4y ≤ 20. where, Origin is included in the region

For equation 2:

Now draw a solid line x = 1 in the graph (because (x = 1) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	0
1	5

Consider x ≥ 1

Lets, select origin point (0, 0)

⇒ 0 ≥ 1

⇒ 0 ≥ 1 (this not is true)

Hence, Solution region of the given inequality is the line x ≥ 1. where, Origin is not included in the region

For equation 3:

Now draw a solid line y = 2 in the graph (because (y = 2) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	2
5	2

Consider y ≥ 2

Lets, select origin point (0, 0)

⇒ 0 ≥ 2

⇒ 0 ≥ 2 (this not is true)

Hence, Solution region of the given inequality is the line y ≥ 2. where, Origin is not included in the region

The graph will be as follows for Equation 1, 2 and 3:

问题10：3x + 4y≤60，x + 3y≤30，x≥0，y≥0

解决方案：

For equation 1:

Now draw a solid line 3x + 4y = 60 in the graph (because (3x + 4y = 60) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	15
20	0

Consider 3x + 4y ≤ 60

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 60

⇒ 0 ≤ 60 (this is true)

Hence, Solution region of the given inequality is the line 3x + 4y ≤ 60. where, Origin is included in the region

For equation 2:

Now draw a solid line x +3y = 30 in the graph (because (x +3y = 30) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	10
30	0

Consider x +3y ≤ 30

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 30

⇒ 0 ≤ 30 (this is true)

Hence, Solution region of the given inequality is the line x +3y ≤ 30. where, Origin is included in the region

For equation 3:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

For equation 4:

Now draw a solid line y = 0 in the graph (because (y = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
5	0

Consider y ≥ 0

Lets, select point (0,3)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line y ≥ 0. where, the point (0,3) is included in the region.

The graph will be as follows for Equation 1, 2. 3 and 4:

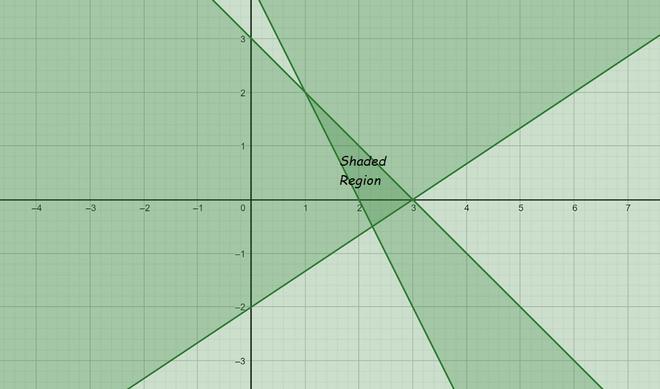
问题11：2x + y≥4，x + y≤3，2x – 3y≤6

解决方案：

For equation 1:

Now draw a solid line 2x + y = 4 in the graph (because (2x + y = 4) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	4
2	0

Consider 2x + y ≥ 4

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 4

⇒ 0 ≥ 4 (this is not true)

Hence, Solution region of the given inequality is the line 2x + y ≥ 4. where, Origin is not included in the region

For equation 2:

Now draw a solid line x + y = 3 in the graph (because (x + y = 3) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	3
3	0

Consider x + y ≤ 3

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 3

⇒ 0 ≤ 3 (this is true)

Hence, Solution region of the given inequality is the line x + y ≤ 3. where, Origin is included in the region

For equation 3:

Now draw a solid line 2x – 3y = 6 in the graph (because (2x – 3y = 6) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	-2
3	0

Consider 2x – 3y ≤ 6

Lets, select origin point (0, 0)

⇒ 0 – 0 ≤ 6

⇒ 0 ≤ 6 (this is true)

Hence, Solution region of the given inequality is the line 2x – 3y ≤ 6. where, Origin is included in the region

The graph will be as follows for Equation 1, 2 and 3:

问题12：x – 2y≤3，3x + 4y≥12，x≥0，y≥1

解决方案：

For equation 1:

Now draw a solid line x – 2y = 3 in the graph (because (x – 2y = 3) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	-1
3	0

Consider x – 2y ≤ 3

Lets, select origin point (0, 0)

⇒ 0 – 0 ≤ 3

⇒ 0 ≤ 3 (this is true)

Hence, Solution region of the given inequality is the line x – 2y ≤ 3. where, Origin is included in the region

For equation 2:

Now draw a solid line 3x + 4y = 12 in the graph (because (3x + 4y = 12) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	3
4	0

Consider 3x + 4y ≥ 12

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 12

⇒ 0 ≥ 12 (this is not true)

Hence, Solution region of the given inequality is the line 3x + 4y ≥ 12. where, Origin is not included in the region

For equation 3:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

For equation 4:

Now draw a solid line y = 1 in the graph (because (y = 1) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	1
5	1

Consider y ≥ 1

Lets, select origin point (0, 0)

⇒ 0 ≥ 1

⇒ 0 ≥ 1 (this is not true)

Hence, Solution region of the given inequality is the line y ≥ 1. where, Origin is not included in the region

The graph will be as follows for Equation 1, 2. 3 and 4:

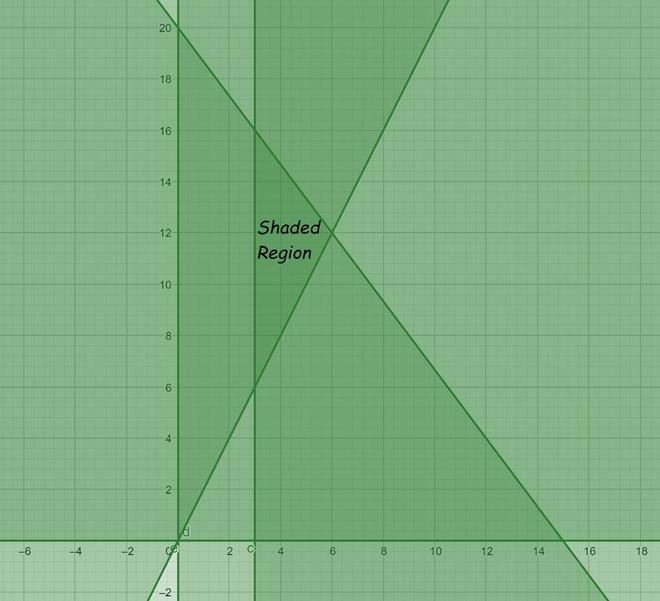
问题13：4x + 3y≤60，y≥2x，x≥3，x，y≥0

解决方案：

For equation 1:

Now draw a solid line 4x + 3y = 60 in the graph (because (4x + 3y = 60) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	20
15	0

Consider 4x + 3y ≤ 60

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 60

⇒ 0 ≤ 60 (this is true)

Hence, Solution region of the given inequality is the line 4x + 3y ≤ 60. where, Origin is included in the region

For equation 2:

Now draw a solid line y = 2x in the graph (because (y = 2x) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
2	4

Consider y ≥ 2x

Lets, select point (3, 0)

⇒ 0 ≥ 6

⇒ 0 ≥ 6 (this is not true)

Hence, Solution region of the given inequality is the line y ≥ 2x. where, the point (3,0) is not included in the region.

For equation 3:

Now draw a solid line x = 3 in the graph (because (x = 3) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
3	0
3	5

Consider x ≥ 3

Lets, select origin point (0, 0)

⇒ 0 ≥ 3

⇒ 0 ≥ 3 (this is not true)

Hence, Solution region of the given inequality is the line x ≥ 3. where, Origin is not included in the region

For equation 4:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

For equation 5:

Now draw a solid line y = 0 in the graph (because (y = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
5	0

Consider y ≥ 0

Lets, select point (0,3)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line y ≥ 0. where, the point (0,3) is included in the region.

The graph will be as follows for Equation 1, 2. 3, 4 and 5:

问题14：3x + 2y≤150，x + 4y≤80，x≤15，y≥0，x≥0

解决方案：

For equation 1:

Now draw a solid line 3x + 2y = 150 in the graph (because (3x + 2y = 150) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	75
50	0

Consider 3x + 2y ≤ 150

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 150

⇒ 0 ≤ 150 (this is true)

Hence, Solution region of the given inequality is the line 3x + 2y ≤ 150. where, Origin is included in the region

For equation 2:

Now draw a solid line x + 4y = 80 in the graph (because (x + 4y = 80) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	20
80	0

Consider x + 4y ≤ 80

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 80

⇒ 0 ≤ 80 (this is true)

Hence, Solution region of the given inequality is the line x + 4y ≤ 80. where, Origin is included in the region

For equation 3:

Now draw a solid line x = 15 in the graph (because (x = 15) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
15	0
15	5

Consider x ≤ 15

Lets, select origin point (0, 0)

⇒ 0 ≤ 15

⇒ 0 ≤ 15 (this is true)

Hence, Solution region of the given inequality is the line x ≤ 15. where, Origin is included in the region

For equation 4:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

For equation 5:

Now draw a solid line y = 0 in the graph (because (y = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
5	0

Consider y ≥ 0

Lets, select point (0,3)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line y ≥ 0. where, the point (0,3) is included in the region.

The graph will be as follows for Equation 1, 2. 3, 4 and 5:

问题15：x + 2y≤10，x + y≥1，x – y≤0，x≥0，y≥0

解决方案：

For equation 1:

Now draw a solid line x + 2y = 10 in the graph (because (x + 2y = 10) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	5
10	0

Consider x + 2y ≤ 10

Lets, select origin point (0, 0)

⇒ 0 + 0 ≤ 10

⇒ 0 ≤ 10 (this is true)

Hence, Solution region of the given inequality is the line x + 2y ≤ 10. where, Origin is included in the region

For equation 2:

Now draw a solid line x + y = 1 in the graph (because (x + y = 1) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	1
1	0

Consider x + y ≥ 1

Lets, select origin point (0, 0)

⇒ 0 + 0 ≥ 1

⇒ 0 ≥ 1 (this is true)

Hence, Solution region of the given inequality is the line x + y ≥ 1. where, Origin is included in the region

For equation 3:

Now draw a solid line x – y = 0 in the graph (because (x – y = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
1	1
0	0

Consider x – y ≤ 0

Lets, select point (3, 0)

⇒ 3 – 0 ≤ 0

⇒ 3 ≤ 0 (this is not true)

Hence, Solution region of the given inequality is the line x – y ≤ 0. where, the point (3,0) is not included in the region

For equation 4:

Now draw a solid line x = 0 in the graph (because (x = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
0	5

Consider x ≥ 0

Lets, select point (3, 0)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line x ≥ 0. where, the point (3,0) is included in the region.

For equation 5:

Now draw a solid line y = 0 in the graph (because (y = 0) is the part of the given equation)

we need at least two solutions of the equation. So, we can use the following table to draw the graph:

x	y
0	0
5	0

Consider y ≥ 0

Lets, select point (0,3)

⇒ 3 ≥ 0

⇒ 3 ≥ 0 (this is true)

Hence, Solution region of the given inequality is the line y ≥ 0. where, the point (0,3) is included in the region.

The graph will be as follows for Equation 1, 2. 3, 4 and 5: