11类NCERT解决方案-第6章线性不等式-第6章的其他练习

解决练习1至6中的不平等问题。

问题1. 2≤3x – 4≤5

解决方案：

In this case, we have two inequalities, 2 ≤ 3x – 4 and 3x – 4 ≤ 5, which we will solve simultaneously. 

We have 2 ≤ 3x – 4 ≤ 5 

or 2 ≤ 3x – 4 and 3x – 4 ≤ 5

⇒ 2 + 4 ≤ 3x and 3x ≤ 5 + 4

⇒ 6 ≤ 3x and 3x ≤ 9

⇒ $\frac{6}{3}$ ≤ x and x ≤ $\frac{9}{3}$

⇒ 2 ≤ x and x ≤ 3

⇒ 2 ≤ x ≤ 3

Hence, all real numbers x greater than or equal to 2 but less than or equal to 3 are solution of given 2 ≤ 3x – 4 ≤ 5 equality.

x ∈ [2, 3]

问题2。6≤– 3(2x – 4)<12

解决方案：

In this case, we have two inequalities, 6 ≤ – 3 (2x – 4) and – 3 (2x – 4) < 12, which we will solve simultaneously.

We have 6 ≤ – 3 (2x – 4) < 12

or 6 ≤ – 3 (2x – 4) and – 3 (2x – 4) < 12

⇒ $\frac{6}{3}$ ≤ -(2x – 4) and -(2x – 4) < $\frac{12}{3}$

⇒ 2 ≤ -(2x – 4) and -(2x – 4) < 4

⇒ -2 ≥ (2x – 4) and (2x – 4) > -4   [multiplying the inequality with (-1) which changes the inequality sign]

⇒ -2+4 ≥ 2x and 2x > -4+4

⇒ 2 ≥ 2x and 2x > 0

⇒ $\frac{2}{2}$ ≥ x > $\frac{0}{2}$

⇒ 1≥ x > 0

⇒ 0 < x ≤ 1

Hence, all real numbers x greater than 0 but less than or equal to 1 are solution of given 6 ≤ – 3 (2x – 4) < 12 equality.

x ∈ (0, 1]

问题3. -3≤4- 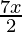$\frac{7x}{2}$ ≤18

解决方案：

In this case, we have two inequalities, -3 ≤ 4- $\frac{7x}{2}$ and 4- $\frac{7x}{2}$ ≤ 18, which we will solve simultaneously.

We have -3 ≤ 4- $\mathbf{\frac{7x}{2}}$ ≤ 18

or -3 ≤ 4- $\frac{7x}{2}$ and 4- $\frac{7x}{2}$ ≤ 18

⇒ -3-4 ≤ – $\frac{7x}{2}$ and – $\frac{7x}{2}$} ≤ 18-4

⇒ -7 ≤ – $\frac{7x}{2}$ and – $\frac{7x}{2}$ ≤ 14

⇒ 7 ≥ $\frac{7x}{2}$ and $\frac{7x}{2}$ ≥ -14   [multiplying the inequality with (-1) which changes the inequality sign]

⇒ 7×2 ≥ 7x and 7x ≥ -14×2 

⇒ $\frac{14}{7}$ ≥ x and x ≥ $\frac{-28}{7}$

⇒ 2 ≥ x ≥ -4

⇒ -4 ≤ x ≤ 2

Hence, all real numbers x greater than or equal to -4 but less than or equal to 2 are solution of given -3 ≤ 4- $\frac{7x}{2}$ ≤ 18 equality.

x ∈ [-4, 2]

问题4. -15 < 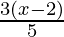$\frac{3(x-2)}{5}$ ≤0

解决方案：

In this case, we have two inequalities, -15 < $\frac{3(x-2)}{5}$ and $\frac{3(x-2)}{5}$} ≤ 0, which we will solve simultaneously.

We have -15 < $\frac{3(x-2)}{5}$ ≤ 0

or -15 < $\frac{3(x-2)}{5}$ and $\frac{3(x-2)}{5}$ ≤ 0

⇒ -15×$\frac{5}{3}$ < (x-2) and (x-2) ≤ 0×$\frac{5}{3}$

⇒ -25 < x-2 and x-2 ≤ 0

⇒ -25+2 < x and x ≤ 0+2

⇒ -23 < x ≤ 2

Hence, all real numbers x greater than -23 but less than or equal to 2 are solution of given -15 ≤ $\frac{3(x-2)}{5}$ ≤ 0 equality.

x ∈ (-23, 2]

问题5. -12 <4-( 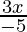$\frac{3x}{-5}$ )≤2

解决方案：

In this case, we have two inequalities, -12 < 4- $\frac{3x}{-5}$ and 4- $\frac{3x}{-5}$ ≤ 2, which we will solve simultaneously.

We have -12 < 4- $\mathbf{\frac{3x}{-5}}$ ≤ 2

or -12 < 4- $\frac{3x}{-5}$ and 4- $\frac{3x}{-5}$ ≤ 2

⇒ -12-4 < $- \frac{3x}{-5}$ and $- \frac{3x}{-5}$ ≤ 2-4

⇒ -16 < $-\frac{3x}{-5}$ and $-\frac{3x}{-5}$ ≤ -2

⇒ -16 < $\frac{3x}{5}$ and $\frac{3x}{5}$ ≤ -2 

⇒ -16×5 < 3x and 3x ≤ -2×5 

⇒ $\frac{-80}{3}$ < x and x ≤ $\frac{-10}{3}$

⇒ $\mathbf{\frac{-80}{3} < x \le \frac{-10}{3}}$

Hence, all real numbers x greater than -80/3 but less than or equal to -10/3 are solution of given -12 < 4- $\frac{3x}{-5}$ ≤ 2 equality.

x ∈ (-80/3, -10/3]

问题6. 7≤ 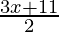$\frac{3x+11}{2}$ ≤11

解决方案：

In this case, we have two inequalities, 7 ≤ $\frac{3x+11}{2}$ and $\frac{3x+11}{2}$ ≤ 11, which we will solve simultaneously.

We have 7 ≤ $\mathbf{\frac{3x+11}{2}}$ ≤ 11

or 7 ≤ $\frac{3x+11}{2}$ and $\frac{3x+11}{2}$ ≤ 11

⇒ 7×2 ≤ 3x+11 and 3x+11 ≤ 11×2

⇒ 14 ≤ 3x+11 and 3x+11 ≤ 22

⇒ 14-11 ≤ 3x and 3x ≤ 22-11

⇒ 3 ≤ 3x and 3x ≤ 11

⇒ 1 ≤ x and x ≤ $\frac{11}{3}$

⇒ 1 ≤ x ≤ $\mathbf{\frac{11}{3}}$

Hence, all real numbers x greater than or equal to 1 but less than or equal to 11/3 are solution of given 7 ≤ $\frac{3x+11}{2}$ ≤ 11 equality.

x ∈ [1, 11/3]

解决练习7至10中的不等式，并在数字线上以图形方式表示解决方案。

问题7：5x +1> – 24，5x – 1 <24

解决方案：

So, from given data

5x + 1 > – 24 ……………………(1)

5x – 1 < 24 …………………….(2)

From inequality (1), we have

5x + 1 > – 24

5x > – 24-1

x > – 25/5

x > -5 ………………………….(3)

Also, from inequality (2), we have

5x – 1 < 24

5x < 24+1

x < 25/5

x < 5 ……………………………(4)

So, from (3) and (4), we can conclude that,

-5 < x < 5 ……………….(5)

If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are 

x ∈ (-5,5)

Thus, solution of the system are real numbers x lying between -5 and 5 excluding -5 and 5.

问题8. 2(x – 1) 2 – x

解决方案：

So, from given data

2 (x – 1) < x + 5 ……………………(1)

3 (x + 2) > 2 – x …………………….(2)

From inequality (1), we have

2 (x – 1) < x + 5

2x – 2 < x + 5

2x – x < 5+2

x < 7 ………………………….(3)

Also, from inequality (2), we have

3 (x + 2) > 2 – x

3x + 6 > 2 – x

3x + x > 2 – 6

4x > -4

x > -1 ……………………………(4)

So, from (3) and (4), we can conclude that,

-1 < x < 7 ……………….(5)

If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are

x ∈ (-1,7)

Thus, solution of the system are real numbers x lying between -1 and 7 excluding -1 and 7.

问题9. 3x – 7> 2(x – 6)，6 – x> 11 – 2x

解决方案：

So, from given data

3x – 7 > 2 (x – 6) ……………………(1)

6 – x > 11 – 2x …………………….(2)

From inequality (1), we have

3x – 7 > 2 (x – 6)

3x – 7 > 2x – 12

3x – 2x > – 12+7

x > -5 ………………………….(3)

Also, from inequality (2), we have

6 – x > 11 – 2x

– x+2x > 11 -6

x > 5 ……………………………(4)

So, from (3) and (4), we can conclude that,

5 < x  ……………….(5)

If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are

x ∈ (5,∞)

Thus, solution of the system are real numbers x lying between 5 and ∞ excluding 5 .

问题10. 5(2x – 7)– 3(2x + 3)≤0，2x + 19≤6x + 47

解决方案：

So, from given data

5 (2x – 7) – 3 (2x + 3) ≤ 0 ……………………(1)

2x + 19 ≤ 6x + 47 …………………….(2)

From inequality (1), we have

5 (2x – 7) – 3 (2x + 3) ≤ 0

10x – 35 -6x – 9 ≤ 0

4x – 44 ≤ 0

4x ≤ 44

x ≤ 44/4

x ≤ 11 ………………………….(3)

Also, from inequality (2), we have

2x + 19 ≤ 6x + 47

2x – 6x ≤ 47 – 19

-4x ≤ 28

4x ≥ -28  [multiplying the inequality with (-1) which changes the inequality sign]

x ≥ -28/4

x ≥ -7 ……………………………(4)

So, from (3) and (4), we can conclude that,

-7 ≤ x ≤ 11 ……………….(5)

If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are

x ∈ [-7,11)

Thus, solution of the system are real numbers x lying between -7 and 11 including -7 and 11 .

问题11.溶液应保持在68°F至77°F之间。如果摄氏度/华氏度(F)转换公式为F =( 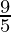$\frac{9}{5}$ C + 32

解决方案：

According to the given data

The solution has to be kept between 68° F and 77° F

So, we have,

68° < F < 77°

Substituting, F = $\mathbf{\frac{9}{5}}$ C + 32

⇒ 68° < $\frac{9}{5}$C + 32 < 77°

⇒ 68°- 32° < $\frac{9}{5}$C < 77°- 32°

⇒ 36° < $\frac{9}{5}$C < 45°

⇒ 36×$\frac{5}{9}$ < C < 45×$\frac{5}{9}$

⇒ 20° < C < 25°

Hence, here we get,

The range of temperature in degree Celsius is between 20° C to 25° C.

问题12.将8％的硼酸溶液加入2％的硼酸溶液进行稀释。所得混合物应大于4％但小于6％的硼酸。如果我们有640升的8％溶液，那么必须添加多少升的2％溶液?

解决方案：

According to the given data,

Here, 8% of solution of boric acid = 640 litres

So, we can take the amount of 2% boric acid solution added as x litres

Hence, Total mixture = (x + 640) litres

As it is given,

The resulting mixture has to be more than 4% but less than 6% boric acid

⇒ (2% of x + 8% of 640) > (4% of (x + 640)) and (2% of x + 8% of 640) < (6% of (x + 640))

⇒ ($\frac{4}{100}$) × (x + 640) < ($\frac{2}{100}$) × x + ($\frac{8}{100}$) × 640) < ($\frac{6}{100}$) × (x + 640)

⇒ 4(x + 640) < (2×x + 8× 640) < 6(x + 640)

⇒ 4x + 2560 < 2x +5120 < 6x+3840

In this case, we have two inequalities, 

⇒ 4x + 2560 < 2x +5120 and 2x +5120 < 6x+3840

⇒ 4x – 2x < 5120 – 2560 and 5120-3840 < 6x-2x

⇒ 2x < 2560 and 1280 < 4x

⇒ x < 2560/2 and 1280/4 < x

⇒ x < 1280 and 320 < x

⇒ 320 < x < 1280

Therefore, the number of litres of 2% of boric acid solution that has to be added will be more than 320 litres but less than 1280 litres.

问题13.必须将多少公升的水添加到1125公升的45％的酸溶液中，以便所得混合物中的酸含量超过25％但少于30％?

解决方案：

According to the given data,

Here, 45% of solution of acid = 1125 litres

Let the amount of water added in the solution = x litres

Resulting mixture = (x + 1125) litres

As it is given,

The resulting mixture has to be more than 25% but less than 30% acid content

Amount of acid in resulting mixture = 45% of 1125 litres.

⇒ 45% of 1125 < 30% of (x + 1125) and 45% of 1125 > 25% of (x + 1125)

⇒ 25% of (x + 1125) < 45% of 1125 < 30% of (x + 1125)

In this case, we have two inequalities, 

⇒ ($\frac{25}{100}$ × (x + 1125)) < ($\frac{45}{100}$ × 1125) and ($\frac{30}{100}$ × (x + 1125)) > ($\frac{45}{100}$ × 1125)

⇒ (25(x + 1125)) < (45×1125) and (30(x + 1125)) > (45×1125)

⇒ (x + 1125) < (45×1125)/25 and (x + 1125) > (45×1125)/30

⇒ (x + 1125) < 2025 and (x + 1125) > 3375/2

⇒ 3375/2 < (x + 1125) < 2025

⇒ (3375/2)-1125 < x < 2025-1125

⇒ 1125/2 < x < 900

⇒ 562.5 < x < 900

Therefore, the number of litres of water that has to be added will have to be more than 562.5 litres but less than 900 litres.

问题14.一个人的智商由以下公式给出： IQ =( 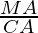$\frac{MA}{CA}$ )×100，其中MA为精神年龄，CA为时间年龄。如果一组12岁的儿童的80≤IQ≤140，请确定其心理年龄的范围。

解决方案：

According to the given data, we have

Chronological age = CA = 12 years

IQ for age group of 12 is in the range, 

80 ≤ IQ ≤ 140

Substituting, IQ = ($\mathbf{\frac{MA}{CA}}$) × 100

⇒ 80 ≤ $\frac{MA}{CA}$ × 100 ≤ 140

⇒ 80 ≤ $\frac{MA}{12}$ × 100 ≤ 140

⇒ 80×12/100 ≤ MA ≤ 140×12/100

⇒ 96/10 ≤ MA ≤ 168/10

⇒ 9.6 ≤ MA ≤ 16.8

Hence, Range of mental age (MA) of the group of 12 years old children is 9.6 ≤ MA ≤ 16.8