通过对所有n∈N使用数学归纳原理证明以下内容:
问题1:1 + 3 + 3 2 +…….. + 3 n-1 = 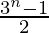
解决方案:
We have,
P(n) = 1 + 3 + 32 + …….. + 3n-1 = ![]()
For n=1, we get
P(1) = 1 = ![]()
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 3 + 32 + …….. + 3k-1 = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 3 + 32 + …….. + 3k-1 + 3(k+1)-1
= (1 + 3 + 32 + …….. + 3k-1) + 3k
From Eq(1), we get
= ![]() + 3k
+ 3k
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题2:1 + 2 3 + 3 3 +……….. + n 3 = ![由QuickLaTeX.com渲染 [\frac{n(n+1)}{2} ]^2](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20NCERT%20Solutions-%20Chapter%204%20Principal%20of%20Mathematical%20Induction%20%E2%80%93%20Exercise%204.1%20%7C%20Set%201_9.jpg)
解决方案:
We have,
P(n) = 1 + 23 + 33 + ……….. + n3 = ![]()
For n=1, we get
P(1) = 1 = ![]() = 1
= 1
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 23 + 33 + ……….. + k3 = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 23 + 33 + ……….. + k3 + (k+1)3
= (1 + 23 + 33 + ……….. + k3) + (k+1)3
From Eq(1), we get
= ![]() + (k+1)3
+ (k+1)3
= ![]() + (k+1)3
+ (k+1)3
= ![]()
Taking (k+1)2, we get
= ![]()
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题3:1 + 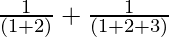 +……。 +
+……。 + 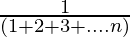 =
= 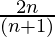
解决方案:
We have,
P(n) = 1 + ![]() =
= ![]()
For n=1, we get
P(1) = 1 = ![]() = 1
= 1
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + ![]() =
= ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + ![]() +
+ ![]()
= (1 + ![]() ) +
) + ![]()
From Eq(1), we get
= ![]()
As we know that,
Sum of first natural number,
1 + 2 + 3 + …… + n = ![]()
So, we get
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题4:1.2.3 + 2.3.4 +…+ n(n + 1)(n + 2)= 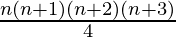
解决方案:
We have,
P(n) = 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) = ![]()
For n=1, we get
P(1) = 1.2.3 = ![]() =
= ![]() = 1.2.3
= 1.2.3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) + (k+1)(k+1+1) (k+1+2)
= (1.2.3 + 2.3.4 +…+ k(k+1) (k+2)) + (k+1)(k+2) (k+3)
From Eq(1), we get
= ![]() + (k+1)(k+2)(k+3)
+ (k+1)(k+2)(k+3)
= (k+1)(k+2) (k+3) (![]() + 1)
+ 1)
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题5:1.3 + 2.3 2 + 3.3 3 +…+ n.3 n = 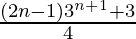
解决方案:
We have,
P(n) = 1.3 + 2.32 + 3.33 +…+ n.3n = ![]()
For n=1, we get
P(1) = 1.3 = 3 = ![]() = 3
= 3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.3 + 2.32 + 3.33 +…+ k.3k = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.3 + 2.32 + 3.33 +…+ k.3k + (k+1).3(k+1)
= (1.3 + 2.32 + 3.33 +…+ k.3k) + (k+1).3(k+1)
From Eq(1), we get
= ![]() + (k+1).3(k+1)
+ (k+1).3(k+1)
= ![]()
= 3k+1 ![]()
= 3k+1 ![]()
= 3k+1 ![]()
= 3(k+1)+1 ![]()
Hence,
P(k+1) = 3(k+1)+1 ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题6:1.2 + 2.3 + 3.4 +…+ n。(n + 1)= ![由QuickLaTeX.com渲染 [\frac{n(n+1)(n+2)}{3}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20NCERT%20Solutions-%20Chapter%204%20Principal%20of%20Mathematical%20Induction%20%E2%80%93%20Exercise%204.1%20%7C%20Set%201_64.jpg)
解决方案:
We have,
P(n) = 1.2 + 2.3 + 3.4 +…+ n.(n+1) = ![]()
For n=1, we get
P(1) = 1.2 = 2 = ![]() = 2
= 2
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2 + 2.3 + 3.4 +…+ k.(k+1) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2 + 2.3 + 3.4 +…+ k.(k+1) + (k+1)(k+1+1)
= (1.2 + 2.3 + 3.4 +…+ k.(k+1)) + (k+1)(k+2)
From Eq(1), we get
= ![]() + (k+1)(k+2)
+ (k+1)(k+2)
= ![]()
= (k+1)(k+2) ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题7:1.3 + 3.5 + 5.7 +…+(2n–1)(2n + 1)= 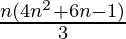
解决方案:
We have,
P(n) = 1.3 + 3.5 + 5.7 +…+ (2n–1) (2n+1) = ![]()
For n=1, we get
P(1) = 1.3 = 3 = ![]() =
= ![]() = 3
= 3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1) + (2(k+1)-1)(2(k+1)+1)
= (1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1)) + (2k+1)(2k+3)
From Eq(1), we get
= ![]() + (4k2+8k+3)
+ (4k2+8k+3)
= ![]()
= ![]()
= ![]()
=![]()
= ![]()
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题8:1.2 + 2.2 2 + 3.2 3 +…+ n.2 n =(n–1)2 n +1 + 2
解决方案:
We have,
P(n) = 1.2 + 2.22 + 3.23 + …+n.2n = (n–1) 2n + 1 + 2
For n=1, we get
P(1) = 1.2 = 2 = (1–1) 2(1) + 1 + 2 = 2
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2 + 2.22 + 3.23 + …+k.2k = (k–1) 2k + 1 + 2 ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2 + 2.22 + 3.23 + …+k.2k + (k+1).2(k+1)
= (1.2 + 2.22 + 3.23 + …+k.2k) + (k+1).2(k+1)
From Eq(1), we get
= (k–1) 2k + 1 + 2 + (k+1).2k+1
= 2k + 1((k–1) + (k+1)) + 2
= 2k + 1(2k) + 2
= k.2k+1+1 + 2
= ((k+1)-1).2(k+1)+1 + 2
Hence,
P(k+1) = ((k+1)-1).2(k+1)+1 + 2
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题9: 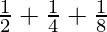 +……+
+……+ 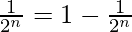
解决方案:
We have,
P(n) = ![]()
For n=1, we get
P(1) = ![]() = 1 –
= 1 – ![]() =
= ![]()
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = ![]()
= (![]() ) +
) + ![]()
From Eq(1), we get
= 1 – ![]()
= 1 – ![]()
= 1 – ![]()
= 1 – ![]()
= 1 –![]()
Hence,
P(k+1) = 1 – ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题10: 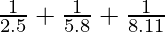 +……+
+……+ 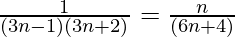
解决方案:
We have,
P(n) = ![]()
For n=1, we get
P(1) = ![]()
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = ![]()
= (![]() ) +
) + ![]()
From Eq(1), we get
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题11: 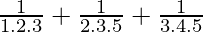 +……+
+……+ 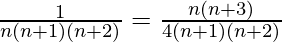
解决方案:
We have,
P(n) = ![]()
For n=1, we get
P(1) = ![]()
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = ![]()
= (![]() ) +
) + ![]()
From Eq(1), we get
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题12:a + ar + ar 2 +……+ ar n-1 = 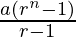
解决方案:
We have,
P(n) = a + ar + ar2 + …… + arn-1 = ![]()
For n=1, we get
P(1) = a = ![]() = a
= a
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = a + ar + ar2 + …… + ark-1 = ![]() ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = a + ar + ar2 + …… + ark-1 + ar(k+1)-1
= (a + ar + ar2 + …… + ark-1) + ark
From Eq(1), we get
= ![]() + ark
+ ark
= ![]()
= ![]()
= ![]()
Hence,
P(k+1) = ![]()
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
问题13:(1+ 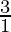 )(1+
)(1+ 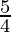 )(1+
)(1+ 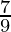 )…..(1+
)…..(1+ 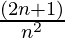 )=(n + 1) 2
)=(n + 1) 2
解决方案:
We have,
P(n) = ![]() = (n+1)2
= (n+1)2
For n=1, we get
P(1) = 1+ ![]() = 1+3 = 4 = (1+1)2 = 22 = 4
= 1+3 = 4 = (1+1)2 = 22 = 4
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = ![]() = (k+1)2 ……………..(1)
= (k+1)2 ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = ![]()
= ![]()
From Eq(1), we get
= (k+1)2 (1+![]() )
)
= (k+1)2 ![]()
= (k+1)2 + 2(k+1) + 1
= {(k+1)}2
Hence,
P(k+1) = {(k+1)}2
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.