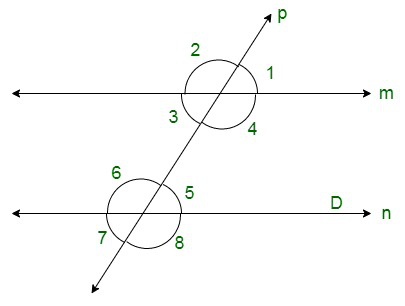
问题21.在给定图中,横向l与两条直线相交,∠4= 110°,∠7= 65°。是|| n?
解决方案:
The figure is given as follows:
It is given that l is a transversal to lines m and n. Also,
∠4 = 110° and ∠7 = 65°
We need to check whether m || n or not.
We have ∠7 = 65°.
Also, ∠7 and ∠5 are vertically opposite angles, thus, these two must be equal. That is,
∠5 = 65° ………(i)
Also, ∠4 = 110°.
Adding this equation to (i), we get:
∠4 + ∠5 = 110° + 65°
∠4 + ∠5 = 175°
But these are the consecutive interior angles which are not supplementary.
Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Thus, m is not parallel to n.
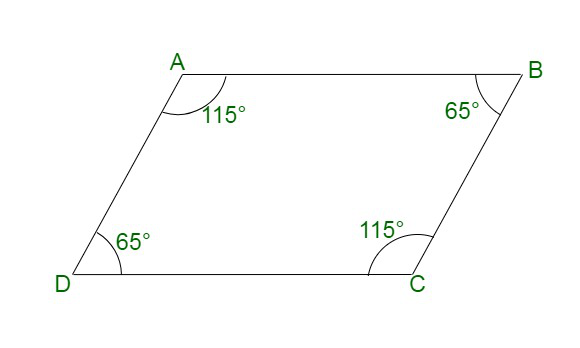
问题22.给定图中的哪两条线是平行的?给出原因。
解决方案:
The figure is given as follows:
We have ∠BCD = 115° and ∠ADC = 65°.
Clearly,
∠BCD + ∠ADC = 115° + 65°
∠BCD + ∠ADC = 180°.
These are the pair of consecutive interior angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Thus, AD || BC.
Similarly, we have ∠DAB = 115° and ∠ADC = 65°.
Clearly,
∠DAB + ∠ADC = 115° + 65°
∠DAB + ∠ADC = 180°.
These are the pair of consecutive interior angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Thus, AB || CD.
Hence, the lines which are parallel are as follows:
AD || BC and AB || CD.
问题23.如果l,m,n是三行,则l || m和n⊥l。证明n⊥m。
解决方案:
The figure can be drawn as follows:
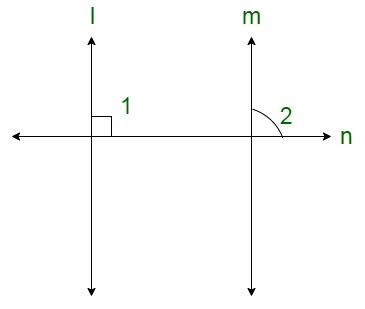
Here, l || m and n ⊥ l
We need to prove that n ⊥ m.
It is given that n ⊥ l, therefore,
∠1 = 90° ……(i)
We have l || m, thus, ∠1 and ∠2 are the corresponding angles. Therefore, these must be equal. That is,
∠1 = ∠2
From equation (i), we get:
∠2 = 90°
Therefore, n ⊥ m.
Hence, proved.
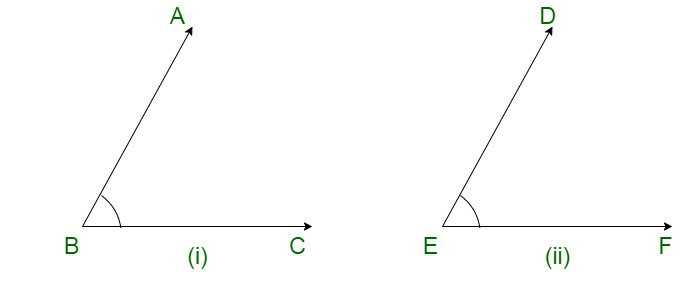
问题24.在给定的图中,∠ABC的手臂BA和BC分别与∠DEF的ED和EF平行。证明∠ABC=∠DEF
解决方案:
The figure is given as follows:
It is given that, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF..
We need to show that ∠ABC = ∠DEF
Let us extend BC to meet EF.
We have AB || DE ∠ABC and ∠DEF are corresponding angles, these two should be equal.
Therefore,
∠ABC = ∠DEF
Hence, proved.
问题25.在给定图中,ABC的BA和BC臂分别与DEF的ED和EF臂平行。证明∠ABC+∠DEF= 180°

解决方案:
The figure is given as follows:
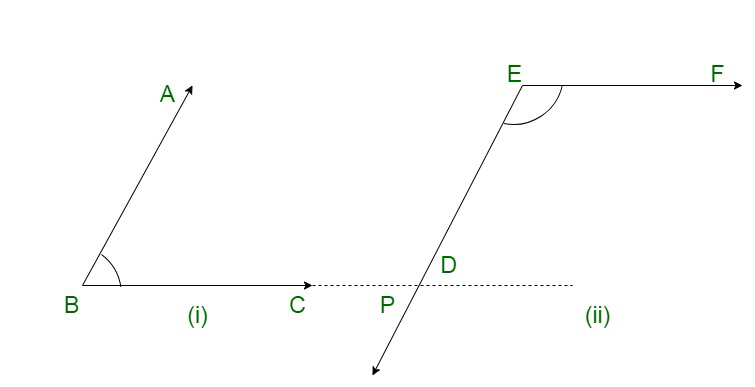
It is given that, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF.
We need to show that ∠ABC + ∠DEF = 180°
Let us extend BC to meet ED at point P.
We have AB || DE and BP || EF. So, ∠BPE and ∠PEF are corresponding angles, these two should be equal.
Therefore,
∠BPE = ∠PEF
Also, we have AB || PE. So, ∠ABP and ∠BPE are consecutive interior angles, these two must be supplementary.
Therefore,
∠ABP + ∠BPE = 180°
∠ABC + ∠PEF = 180°
∠ABC + ∠DEF = 180°
Hence, proved.
问题26.以下哪些陈述是正确的(T),哪些是错误的(F)?说明原因。
(i)如果两条线被一个横向线相交,则相应的角度相等。
(ii)如果两条平行线被一个横向线相交,则交替的内角相等。
(iii)垂直于同一条线的两条线彼此垂直。
(iv)两条平行于同一条线的线彼此平行。
(v)如果两条平行线被一个横向线相交,则横向线同一侧的内角相等。
解决方案:
(i) Statement: If two lines are intersected by a transversal, then corresponding angles are equal.
False
Reason: The above statement holds good if the lines are parallel only.
(ii) Statement: If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
True
Reason: Letlandmare two parallel lines.
And transversaltintersectslandmmakinga two pair of alternate interior angles, ∠1, ∠2 and ∠3, ∠4
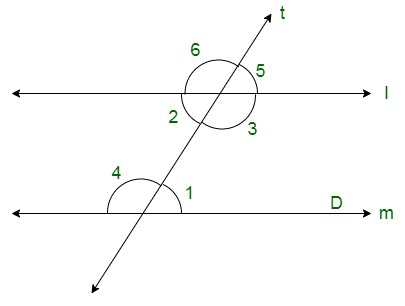
We need to prove that ∠1 = ∠2 and ∠3 = ∠4.
We have,
∠2 = ∠5 (Vertically opposite angles)
And, ∠1 = ∠5 (corresponding angles)
Therefore,
∠1 = ∠2 (Vertically opposite angles)
Again, ∠3 = ∠6 (corresponding angles)
Hence, ∠1 = ∠2 and ∠3 = ∠4.
(iii) Statement: Two lines perpendicular to the same line are perpendicular to each other.
False
Reason:The figure can be drawn as follows:
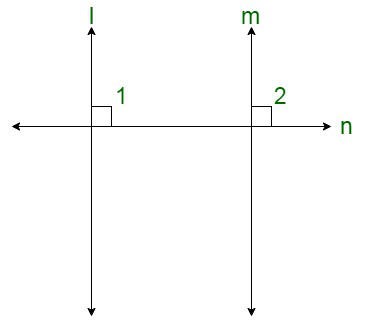
Here, l ⊥ n and m ⊥ n
It is given that l ⊥ n, therefore,
∠1 = 90° …….(i)
Similarly, we have m ⊥n, therefore,
∠2 = 90° …….(ii)
From (i) and (ii), we get:
∠1 = ∠2
But these are the pair of corresponding angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.
Thus, we can say that l || m.
(iv) Statement: Two lines parallel to the same line are parallel to each other.
True
Reason: The figure is given as follows:
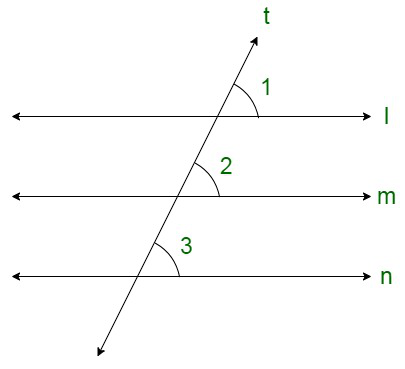
It is given that l || m and m || n
We need to show that l || m
We have l || m, thus, corresponding angles should be equal.
That is,
∠1 = ∠2
Similarly,
∠3 = ∠2
Therefore,
∠1 = ∠3
But these are the pair of corresponding angles.
Therefore, l || m.
(v) Statement: If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are equal.
False
Reason: Theorem states: If a transversal intersects two parallel lines then the pair of alternate interior angles is equal.
问题27.在以下各项中填写空白以使陈述正确:
(i)如果两条平行线被一个横向线相交,则每对对应的角度为…
(ii)如果两条平行线被一个横向线相交,则横向线同一侧的内角为…。
(iii)垂直于同一条线的两条线是…彼此。
(iv)两条平行于同一条线的线彼此…。
(v)如果一个横向线与一对线相交,使得一对交替的角度相等,则这些线为…
(vi)如果一个横向线与一对直线相交,使得横向线同一侧的内角之和为180°,则这些直线为…
解决方案:
(i) If two parallel lines are intersected by a transversal, then corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
(iii) Two lines perpendicular to the same line are parallel to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If a transversal intersects a pair of lines in such a way that a pair of interior angles is equal, then the lines are parallel.
(vi) If a transversal intersects a pair of lines in such a way that a pair of interior angles on the same side of transversal is 180°, then the lines are parallel.