Class 10 NCERT解决方案-第15章概率–练习15.1 |套装1

Theorem 1:

The theoretical probability (also called classical probability) of an event E, written as P(E), is defined as

P(E) = $\frac{Number \hspace{0.1cm}of \hspace{0.1cm}outcomes \hspace{0.1cm}favourable \hspace{0.1cm}to \hspace{0.1cm}E}{Number\hspace{0.1cm} of \hspace{0.1cm}all\hspace{0.1cm} possible \hspace{0.1cm}outcomes \hspace{0.1cm}of \hspace{0.1cm}the \hspace{0.1cm}experiment}$

问题1.完成以下陈述：

(i)事件E的概率+事件’not E’的概率= _________________。

(ii)无法发生的事件的概率是__________。这样的事件称为__________________。

(iii)肯定会发生的事件的概率是______________。此类事件称为_______________。

(iv)实验所有基本事件的概率之和为______________________。

(v)事件发生的概率大于或等于_______________小于或等于____。

解决方案：

(i) 1

(ii) 0, Impossible Event

(iii) 1, Sure Event

(iv) 1

(v) 0, 1

问题2.下列哪个实验有同样可能的结果?解释。

(i)驾驶员试图发动汽车。汽车启动或不启动。

(ii)一名球员试图投篮。她/他射门或射门未中。

(iii)尝试回答是非题。答案是对还是错。

(iv)婴儿出生。是男孩还是女孩。

解决方案：

(i) This statement does not have equally likely outcomes as the car may or may not start depending upon various internal and external factors like fuel, path etc.

(ii) This statement does not have equally likely outcomes as the player may shoot or miss the shot depending upon various factors.

(iii) This statement has equally likely outcomes as it is known that the solution is either right or wrong, both have equal chance to happen.

(iv) This statement also has equally likely outcomes as it is known that the newly born baby can either be a boy or a girl, both have equal chance to happen.

问题3：为什么抛硬币被认为是决定哪支球队在足球比赛开始时应该接球的公平方法?

解决方案：

Tossing of a coin is a fair way of deciding because they have equally likely outcomes where the number of possible outcomes are only 2 i.e. either head or tail. Tossing is considered to be completely unbiased and is unpredictable .

问题4.以下哪一项不能成为事件的概率?

(A)2/3

(B)-1.5

(C)15％

(D)0.7

解决方案：

As the probability of any event (E) always lies between 0 and 1 

i.e. 0 ≤ P(E) ≤ 1

(i) 2/3 can be the probability of an event.

(ii) -1.5 cannot be the probability of an event.

(iii) 15% can be the probability of an event.

(iv) 0.7 can be the probability of an event.

问题5.如果P(E)= 0.05，那么“非E”的概率是多少?

解决方案：

As, P(E) + P(not E) = 1

⇒ P(Not E) = 1 – P(E) (Where the event ‘not E’ is complement of the event E)

Here, P(E) = 0.05

Then, P(Not E) = 1 – 0.05

P(Not E) = 0.95

问题6.一袋仅包含柠檬味的糖果。马里尼不看袋子就拿出一个糖果。她拿出来的几率是多少

(i)橙味糖果?

(ii)柠檬味糖果?

解决方案：

(i) As we know that the bag contains lemon-flavored candies only.

Hence, the no. of orange flavored candies = 0

The probability of taking out orange flavored candies = $\frac{0}{1}$ …………………… (from Theorem 1) 

= 0 (Impossible Event)

(ii) As there are only lemon flavored candies, 

P(Lemon flavored candies) = 1 (Sure Event)

问题7.假设在3个学生的组中，有2个学生的生日不同的概率为0.992。这两个学生有相同生日的概率是多少?

解决方案：

As, P(E) + P(not E) = 1

⇒ P(E) = 1 – P(Not E) (Where the event ‘not E’ is complement of the event E)

Here, P(Not E) = Probability of 2 students not having the same birthday = 0.992

Here, P(E) = Probability that the 2 students have the same birthday

Then, P(E) = 1 – 0.992

P(E) = 0.08

Hence, the probability that the 2 students have the same birthday is 0.008

问题8.一个袋子包含3个红球和5个黑球。从袋子中随机抽出一个球。抽出球的几率是多少

(i)红色?

(ii)不是红色?

解决方案：

Number of Red balls = 3

Number of Black balls = 5

Total number of balls = 5+3 = 8

Hence, total number of possible outcomes = 8

(i) P(E) = Probability that the ball drawn is Red.

P(E) = $\frac{3}{8}$ ……………..(From Theorem 1)

(ii) P(Not E) = Probability that the ball drawn is not Red

P(Not E) = 1 – P(E) (Where the event ‘not E’ is complement of the event E)

P(Not red) = 1-$\frac{3}{8}$ = $\frac{5}{8}$

问题9.一个盒子装有5个红色大理石，8个白色大理石和4个绿色大理石。随机从包装盒中取出一种大理石。取出大理石的概率是多少

(i)红色?

(ii)白色?

(iii)不是绿色的吗?

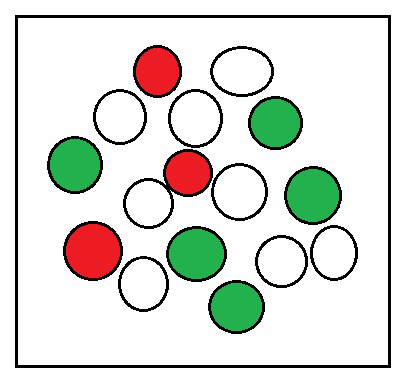
解决方案：

Number of Red balls = 5

Number of White balls = 8

Number of Green balls = 4

Total number of balls = 5+8+4 = 17

Hence, total number of possible outcomes = 17

(i) P(E) = Probability that the ball drawn is Red.

P(E) = $\frac{5}{17}$ …………….. (From Theorem 1)

(ii) P(E) = Probability that the ball drawn is White.

P(E) = $\frac{8}{17}$ …………….. (From Theorem 1)

(iii) Let P(E) = Probability that the ball drawn is not Green.

P(E) = $\frac{4}{17}$………. (From Theorem 1)

P(Not E) = 1 – P(E) (Where the event ‘not E’ is complement of the event E)

P(Not Green) = 1-$\frac{4}{17}$ = $\frac{13}{17}$

问题10.存钱罐包含一百个50p硬币，五十个₹1硬币，二十个₹2硬币和十个₹5硬币。如果银行倒置时，硬币中的一种可能掉出的可能性相同，那么硬币的概率是多少?

(i)是50便士硬币吗?

(ii)会不会是₹5硬币?

解决方案：

Number of 50p coins = 100

Number of ₹1 coins = 50

Number of ₹2 coins = 20

Number of ₹5 coins = 10

Total number of coins = 100+50+20+10 = 180

Hence, total number of possible outcomes = 180

(i) P(E) = Probability that the coin will be a 50 p coin.

P(E) = $\frac{100}{180} = \frac{5}{9}$…………….. (From Theorem 1)

(ii) Let P(E) = Probability that the coin will be a ₹5 coin.

P(E) = $\frac{10}{180} = \frac{1}{18}$.……………. (From Theorem 1)

Then, P(Not E) = Probability that the coin will not be a ₹5 coin.

P(Not E) = 1 – P(E) (Where the event ‘not E’ is complement of the event E)

P(Not ₹5 coin) = 1-$\frac{1}{18} = \frac{17}{18}$

问题11：戈皮从一家商店购买鱼来养鱼。店主从装有5条雄鱼和8条雌鱼的鱼缸中随机取出一条鱼。取出的鱼是公鱼的概率是多少?

解决方案：

Number of male fish = 5

Number of female fish = 8

Total number of fish in the tank = 5+8 = 13

Hence, total number of possible outcomes = 13

P(E) = Probability that the fish will be male.

P(E) = $\frac{5}{13}$ ………………. (From Theorem 1)

问题12.机会游戏包括旋转箭头，箭头指向静止的数字1、2、3、4、5、6、7、8(见图15.5)之一，这些结果的可能性相同。 。它指向的概率是多少

(i)8?

(ii)奇数?

(iii)大于2的数字?

(iv)小于9的数字?

解决方案：

Here, total number of possible outcomes = 8

(i) P(E) = Probability that pointer will point at 8.

P(E) = $\frac{1}{8}$ ………………. (From Theorem 1)

(ii) P(E) = Probability that pointer will point at an odd number.

Odd number = {1,3,5,7}

P(E) = $\frac{4}{8} = \frac{1}{2}$ ………………. (From Theorem 1)

(iii) P(E) = Probability that pointer will point at a number greater than 2.

Numbers greater than 2 = {3,4,5,6,7,8}

P(E) = $\frac{6}{8} = \frac{3}{4}$ ………………. (From Theorem 1)

(iv) P(E) = Probability that pointer will point at a number less than 9.

Numbers less than 9 = {1,2,3,4,5,6,7,8}

P(E) = $\frac{8}{8}$ = 1 ………………. (From Theorem 1)