10类RD Sharma解决方案–第14章坐标几何–练习14.2 |套装1

问题1.找到以下两对点之间的距离：

(i)(-6、7)和(-1，-5)

(ii)(a + b，b + c)和(a – b，c – b)

(iii)(a sin a，-b cos a)和(-a cos a，b sin a)

(iv)(a，0)和(0，b)

解决方案：

(i) Given that P(-6, 7) and Q(-1, -5)

So, x₁ = -6, y₁ = 7 

x₂ = -1, y₂ = -5

Now we find the distance between PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{[-1-(-6)]^2+(-5-7)^2}\\ PQ=\sqrt{(-1+6)^2+(-5-7)^2}\\ PQ=\sqrt{(5)^2+(-12)^2}\\ PQ=\sqrt{25+144}\\ PQ=\sqrt{169}\\ PQ=13\\$

(ii) Given that P(a + b, b + c) and Q(a – b, c – b) 

So, x₁ = a + b, y₁ = b + c

x₂ = a – b, y₂ = c – b

Now we find the distance between PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{[a-b-(a+b)]^2+(c-b-(b+c))^2}\\ PQ=\sqrt{(a-b-a-b)^2+(c-b-b-c)^2}\\ PQ=\sqrt{(-2b)^2+(-2b)^2}\\ PQ=\sqrt{4b^2+2b^2}\\ PQ=\sqrt{8b^2}\\ PQ=\sqrt{4*2b^2}\\ PQ=2\sqrt{2b}$

(iii) Given that P(a sin a,-b cos a) and Q(-a cos a, b sin a)

So, x₁ = a sin a, y₁ = -b cos a

x₂ = a cos a, y₂ = b sin a

Now we find the distance between PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{(-a\cos a-a\sin a)^2+[-b\sin a-(-b\cos a)]^2}\\ PQ=\sqrt{(-a\cos a)^2+(-a\sin a)^2+2(a-\cos a)(-a\sin a)+(b\sin a)^2+(-b\cos a)^2-2(b\sin a)(-b\cos a)}\\ PQ=\sqrt{a^2cos^2a+a^2\sin^2a+2a^2\cos a\sin a+b^2\sin^2a+b^2\cos^2a+2b^2\sin a\cos a}\\ PQ=\sqrt{a^2(\cos^2a+\sin^2a)+2a^2\cos a\sin a+b^2(\sin^2a+\cos^2a)+2b^2\sin a\cos a}\\ PQ=\sqrt{a^2*1+2a^2\cos a\sin a+b^2*12b^2\sin a\cos a}\\ PQ=\sqrt{a^2+b^2+2a^2\cos a\sin a+2b^2\sin a\cos a}\\ PQ=\sqrt{(a^2+b^2)+2\cos a\sin a(a^2+b^2)}\\ PQ=\sqrt{(a^2+b^2)+(1+2\cos a\sin a)}\\$

(iv) Given that P(a, 0) and Q(0, b)

So, x₁ = a, y₁ = 0

x₂ = 0, y₂ = b

Now we find the distance between PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{(0-a)^2+(b-0)^2}\\ PQ=\sqrt{(-a)^2+(b)^2}\\ PQ=\sqrt{a^2+b^2}\\$

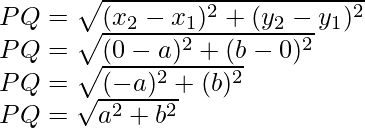
问题2.当点(3，a)和(4，1)之间的距离为√10时，找到a的值。

解决方案：

Given that point P(3, a) and Q(4, 1) and the distance between them is √10

So, we have to find the value of a

So, 

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ \sqrt{10}=\sqrt{(4-3)^2+(1-a)^2}\\ \sqrt{10}=\sqrt{(1)^2(1-a)^2}\\ \sqrt{10}=\sqrt{1+1+a^2-2a}\\ \sqrt{10}=\sqrt{2+a^2-2a}$

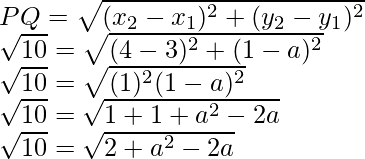
Squaring on both sides we get 

(√10)² = (√{2 + a² – 2a})² 

10 = 2 + a² – 2a

a² – 2a + 2 – 10 = 0

a² – 2a – 8 = 0

On Splitting the middle term we get 

a² – 4a + 2a – 8 = 0

a(a – 4) + 2(a – 4) = 0

(a – 4)(a + 2) = 0 

a = 4, a = -2

问题3.如果点(2，1)和(1，2)与点(x，y)等距，则表明x + 3y = 0。

解决方案：

Given that P(2, 1) and Q(1, -2) and R(x, y)

Also, PR = QR

$PR=\sqrt{(x-2)^2+(y-1)^2}\\ PR=\sqrt{x^2(2)^2-2xx*2+y^2+(1)^2-2*y*1}\\ PR=\sqrt{x^2+4-4x+y^2+1-2y}\\ PR=\sqrt{x^2+5-4x+y^2-2y}\\ QR=\sqrt{(x-1)^2+(y+2)^2}\\ PR=\sqrt{x^2+1-2x+y^2+4+4y}\\ PR=\sqrt{x^2+5-2x+y^2+4y}\\ PR=QR\\ \sqrt{x^2+5-4x+y^2-2y}=\sqrt{x^2+5-2x+y^2+4y}$

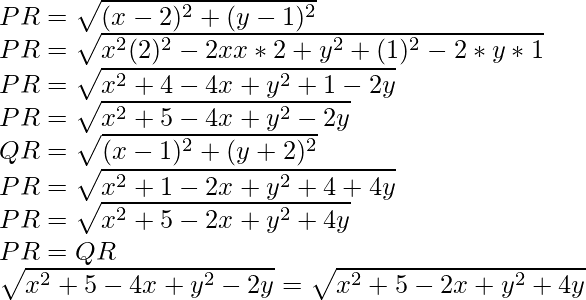
x² + 5 – 4x + y² – 2y = x² + 5 – 2x + y² + 4y

x² + 5 – 4x + y² – 2y = x² + 5 – 2x + y² + 4y 

-4x + 2x – 2y – 4y = 0 

-2x – 6y = 0

 -2(x + 3y) = 0

x + 3y = 0/-2 

x + 3y = 0

Hence Proved

问题4.如果点(x，y)距(-3，0)以及距(3，0)的距离为4，则求x，y的值。

解决方案：

Given that P(x, y), Q(-3, 0) and R(3, 0). 

Also, PQ = PR = 4

So, 

$PQ=\sqrt{(x+3)^2+(y-0)^2}\\ 4=\sqrt{x^2+9+6x+y^2}$

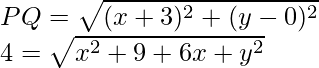
On squaring on both sides, we get 

(4)² = (√x² + 9 + 6x + y²)² 

16 = x² + 9 + 6x + y² 

x² + y² = 16 – 9 – 6x

x² + y² = 7 – 6x ……..(1)

$PR=(\sqrt{(x-3)^2+(y-0)^2})\\ 4=\sqrt{x^2+9-6x+y^2}$

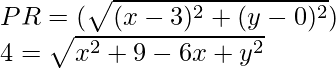
On squaring on both sides, we get

(4)² = (√x² + 9 – 6x + y²)² 

16 = x² + 9 – 6x + y²

x² + y² = 16 – 9 + 6x

x² + y² = 7 + 6x  ……..(2)

From equation (1) and (2)

7 – 6x = 7 + 6x

7 – 7 = 6x + 6x

0 = 12x

x = 12

On substituting the value of x = 0 in eq(2)

x² + y² = 7 + 6x

0 + y² = 7 + 6 * 0

y² = 7

y = ±√7

问题5.线段的长度为10个单位，一个端点的坐标为(2，-3)。如果另一端的横坐标为10，则找到另一端的坐标。

解决方案：

Let the ordinate of other end by y, then The distance between (2, -3) and (10, y) is

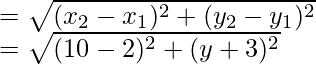$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(10-2)^2+(y+3)^2}$ = 10 

Squaring on both sides we get

(8)² + (y + 3)² = 100

64 + y² + 6y + 9 = 100

y² + 6y + 73 – 100 = 0

y² + 6y – 27 = 0 

y² + 9y – 3y – 27 = 0

y(y + 9) – 3(y + 9) = 0

(y + 9)(y – 3) = 0

When y + 9 = 0, then y = -9

or when y – 3 = 0, then y = 3 

So, the coordinates will be -9 or 3

问题6。证明点(-4，-1)，(-2，-4)，(4、0)和(2、3)是矩形的顶点。

解决方案：

Let us considered ABCD is a rectangle whose vertices are

A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3)

Now 

AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{(-2+4)^2+(-4+1)^2}\\ =\sqrt{(2)^2+(-3)^2}=\sqrt{4+9}=\sqrt{13}$

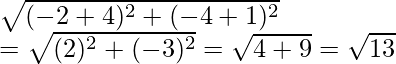
Similarly, CD =√13 

AD = √52

and BC = √52

AC = √65 and BD = √65

Here, AB = CD and AD = BC

and diagonals AC = BD

So, ABCD is a rectangle

问题7.证明点A(1，-2)，B(3、6)，C(5、10)和D(3、2)是平行四边形的顶点。

解决方案：

Given points are A (1, -2), B (3, 6), C (5, 10) and D (3, 2)

Now AB = 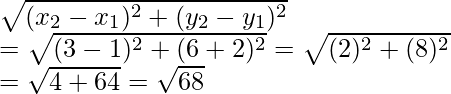$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-1)^2+(6+2)^2}=\sqrt{(2)^2+(8)^2}\\ =\sqrt{4+64}=\sqrt{68}$

Similarly BC = 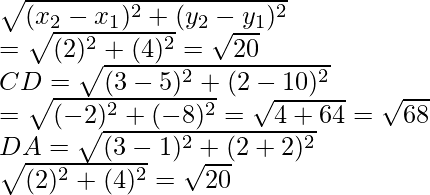$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2)^2+(4)^2}=\sqrt{20}\\ CD=\sqrt{(3-5)^2+(2-10)^2}\\ =\sqrt{(-2)^2+(-8)^2}=\sqrt{4+64}=\sqrt{68} \\DA=\sqrt{(3-1)^2+(2+2)^2}\\ \sqrt{(2)^2+(4)^2}=\sqrt{20}$

So, from the above we conclude that AB = CD and AD = BC

Hence, ABCD is a parallelogram.

问题8.证明点A(1、7)，B(4、2)，C(-1，-1)和D(-4、4)是正方形的顶点。

解决方案：

Given points are A (1, 7), B (4, 2), C (-1,-1), D (-4, 4)

If these are the vertices of a square, then its diagonals and sides are equal

AC = 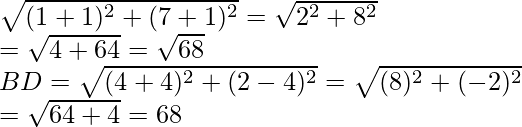$\sqrt{(1+1)^2+(7+1)^2}=\sqrt{2^2+8^2}\\ =\sqrt{4+64}=\sqrt{68}\\ BD=\sqrt{(4+4)^2+(2-4)^2}=\sqrt{(8)^2+(-2)^2}\\ =\sqrt{64+4}=68$

So, AC = BD

Now AB=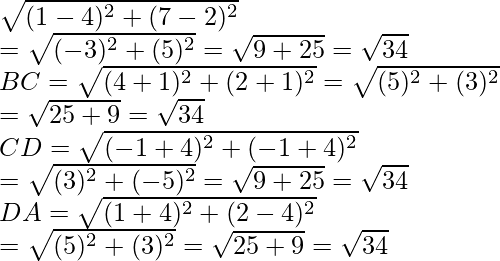$\sqrt{(1-4)^2+(7-2)^2}\\ =\sqrt{(-3)^2+(5)^2}=\sqrt{9+25}=\sqrt{34}\\ BC=\sqrt{(4+1)^2+(2+1)^2}=\sqrt{(5)^2+(3)^2}\\ =\sqrt{25+9}=\sqrt{34}\\ CD=\sqrt{(-1+4)^2+(-1+4)^2}\\ =\sqrt{(3)^2+(-5)^2}=\sqrt{9+25}=\sqrt{34}\\DA=\sqrt{(1+4)^2+(2-4)^2}\\ =\sqrt{(5)^2+(3)^2}=\sqrt{25+9}=\sqrt{34}$

So, AB = BC = CD = DA and diagonal AC = BD

Hence, the given figure ABCD is a square.

问题9证明点(3，0)，(6，4)和(-1，3)是直角等腰三角形的顶点。

解决方案：

Given points are A(3, 0), B(6, 4), and C(-1, 3)

Now we find the length of AB = 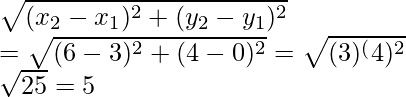$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(6-3)^2+(4-0)^2}=\sqrt{(3)^(4)^2}\\ \sqrt{25}=5$

Similarly, BC=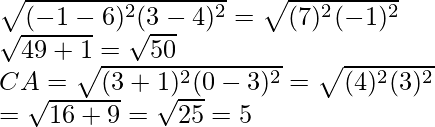$\sqrt{(-1-6)^2(3-4)^2}=\sqrt{(7)^2(-1)^2}\\ \sqrt{49+1}=\sqrt{50}\\ CA=\sqrt{(3+1)^2(0-3)^2}=\sqrt{(4)^2(3)^2}\\ =\sqrt{16+9}=\sqrt{25}=5$

From the above we conclude that AB = CA and BC is the longest side

Now we verify the Pythagoras theorem,

So, BC² = AB² + CA² 

BC² = (5)² + (5)² 

BC² = 25 + 25 

50 = 50

So, AB² + CA² = BC²

Hence, the given triangle ABC is an isosceles right triangle.

问题10.证明(2，-2)，(-2、1)和(5，2)是直角三角形的顶点。找出三角形的面积和斜边的长度。

解决方案：

Given points are A(2, -2), B(-2, 1) and C(5, 2)

Now we find the length of 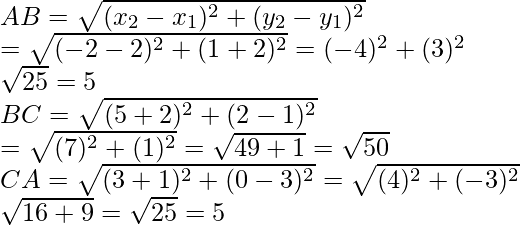$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(-2-2)^2+(1+2)^2}=(-4)^2+(3)^2\\ \sqrt{25}=5\\ BC=\sqrt{(5+2)^2+(2-1)^2}\\ =\sqrt{(7)^2+(1)^2}=\sqrt{49+1}=\sqrt{50}\\ CA=\sqrt{(3+1)^2+(0-3)^2}=\sqrt{(4)^2+(-3)^2}\\ \sqrt{16+9}=\sqrt{25}=5$

We see that AB = CA and BC is the longest side.

Now we verify the Pythagoras theorem,

So, BC² = AB² + CA² 

BC² = (5)² + (5)² 

BC² = 25 + 25 

50 = 50

So, AB² + CA² = BC²

So, the given triangle ABC is a right-angled triangle

Now we find the area of triangle ABC = 1/2 × Base × height 

= 1/2 × 5 × 5

= 25/2 sq.units

And the length of the hypotenuse BC is √50.

问题11。证明点(2a，4a)，(2a，6a)和(2a +√3a，5a)是等边三角形的顶点。

解决方案：

Given points are A(2a, 4a), B(2a, 6a) and C(2a + √3 a, 5a)

Now we find the length of 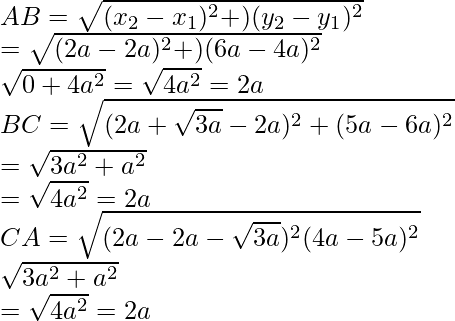$AB=\sqrt{(x_2-x_1)^2+)(y_2-y_1)^2}\\ =\sqrt{(2a-2a)^2+)(6a-4a)^2}\\ \sqrt{0+4a^2}=\sqrt{4a^2}=2a\\ BC=\sqrt{(2a+\sqrt{3a}-2a)^2+(5a-6a)^2}\\ =\sqrt{3a^2+a^2}\\ =\sqrt{4a^2}=2a \\ CA=\sqrt{(2a-2a-\sqrt{3a})^2(4a-5a)^2}\\ \sqrt{3a^2+a^2}\\ =\sqrt{4a^2}=2a$

So, we conclude that the length of side AB = BC = CA = 2a

Hence, ∆ABC is equilateral triangle. 

问题12.证明点(2、3)，(-4，-6)和(1、32)不形成三角形。

Given points are A(2, 3), B(-4, -6), and C(1, 32)

Now we find the length of AB = 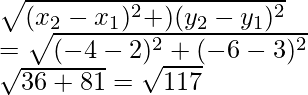$\sqrt{(x_2-x_1)^2+)(y_2-y_1)^2}\\ =\sqrt{(-4-2)^2+(-6-3)^2}\\ \sqrt{36+81}=\sqrt{117}\\$

Similarly, for BC = √89 and CA = √2 

As we know that the sum of two sides of triangle are always greater than the third side

So, BC + CA= √89 + √2 not greater than AB 

Hence, the given points do not form a triangle.

问题13：点A(2，9)，B(a，5)和C(5，5)是三角形ABC在B处成直角的顶点。找到a的值，从而找到∆的面积ABC。

解决方案：

Given that, the points A (2, 9), B (a, 5) and C (5, 5) are the vertices of ∆ABC right-angled at B.

By Pythagoras theorem, 

AC² = AB² + BC² ………(i)

Now, by distance formula,

We find the length of AB = $\sqrt{(a-2)^2+(5-9)^2}$

=$\sqrt{a^2+4-4a+16}=\sqrt{a^2-4a+20}\\ BC=\sqrt{(5-a)^2+(5-5)^2}\\ =\sqrt{(5-a)^2+0}=5-a\\ AC=\sqrt{(2-5)^2+(9-5)^2}\\ =\sqrt{(-3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}=5$]

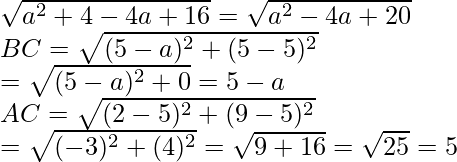Now put the values of AB, BC and AC in equation(i), we get

$(5)^2=\sqrt{(a^2-4a+20)^2+(5-a)^2}$

25 = a² – 4a + 20 + 25 + a² – 10a

2a² – 14a + 20 = 0

a² – 7a + 10 = 0

a² – 2a – 5a + 10 = 0

a(a – 2) – 5(a – 2) = 0

(a – 5)(a – 5) = 0

a = 2, 5

Here, a ≠ 5, since at a = 5, the length of BC = 0. It is not possible because  

the sides AB,BC and CA from a right angled triangle.

So, a = 2

Now, the coordinates are A (2, 9), B (2, 5) and C (5, 5)

Now we find the area of ∆ABC = $\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]$

= 1/2[2(5 – 5) + 2(5 – 9) + 5(9 – 5)]

= 1/2(0 – 8 + 20) 

= 1/2 × 12

= 6

Hence, the required area of ∆ABC is 6sq. units.

问题14.证明顶点为(2，-1)，(3，4)，(-2、3)和(-3，-2)的四边形是菱形。

解决方案：

Given points are A(2, -1), B(3, 4), C(-2, 3), and D(-3, -2)

Now we find the length of sides AB, CD, DA, BD and diagonals AC, BD

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-2)^2+(4+1)^2}=\sqrt{(1)^2+(5)^2}=\sqrt{1+25}=\sqrt{26}\\ BC=\sqrt{(-2-3)^2+(3-4)^2}\\ \sqrt{(-5)^2+(-1)^2}=\sqrt{25+1}=\sqrt{26}\\ CD=\sqrt{(-3+2)^2+(-2-3)^2}=\sqrt{(-1)^2+(-5)^2}=\sqrt{1+25}=\sqrt{26}\\DA=\sqrt{(2+3)^2+(-1+2)^2}\\ =\sqrt{(5)^2+(1)^2}=\sqrt{25+1}=\sqrt{26}\\AC=\sqrt{(-2-2)^2+(3+1)^2}\\ =\sqrt{(-4)^2+(4)^2}=\sqrt{16+16}=\sqrt{32} \\BD=\sqrt{(-3-3)^2+(-2-4)^2}\\ =\sqrt{(-6)^2+(-6)^2}=\sqrt{36+36}=\sqrt{72}$

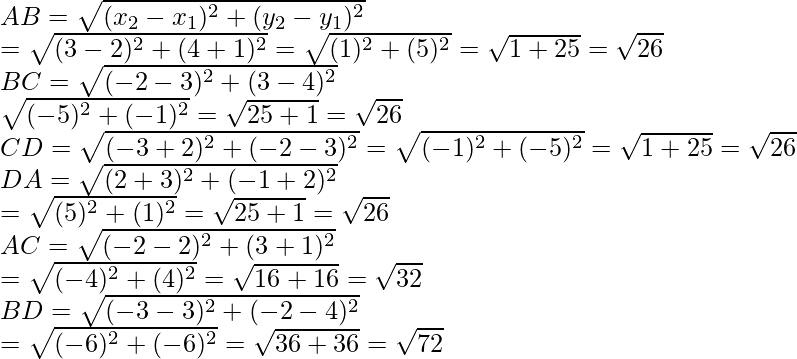
Now we conclude that AB = BC = CD = DA = √26 and diagonal AC ≠ BD

Hence, ABCD is a rhombus

问题15.等腰三角形的两个顶点是(2，0)和(2，5)。如果等边的长度为3，则找到第三个顶点。

解决方案：

Let us considered ABC is an isosceles triangle whose two vertices are A (2, 0) and B (2, 5)

So, the co-ordinates of third vertex C be (x, y)

And also given that AC = BC = 3

Now 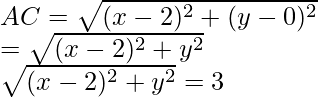$AC=\sqrt{(x-2)^2+(y-0)^2}\\ =\sqrt{(x-2)^2+y^2}\\ \sqrt{(x-2)^2+y^2}=3$

On squaring both sides, we get

(x – 2)² + y² = 9                        

x² – 4x + 4 + y² = 9

x² + y² – 4x =  5             …….(i)

Similarly, 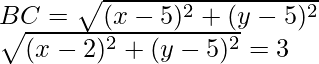$BC=\sqrt{(x-5)^2+(y-5)^2}\\ \sqrt{(x-2)^2+(y-5)^2}=3$

On squaring both sides, we get

(x – 2)² + (y – 5)² = 9               

x² – 4x + 4 + y² – 10y + 25 = 9

x² + y² – 4x – 10y = -20             …….(ii)

Now on subtracting eq(ii) from (i), we get

10y = 25

y = 25/10 = 5/2

On substituting the value of y in eq(i)

x² – 4x + (5/2)² = 5

x² – 4x + 25/4 – 5 = 0

4x² – 16x + 25 – 20 = 0

4x² – 16x + 5 + 5 = 0

Here a = 4, b = -16, c = 5

$x=\frac{-b±\sqrt{b^2-4ac}}{2a}\\ \frac{-(-16)±\sqrt{(-16)^2-4\times 4\times 5}}{2\times 4}\\ =\frac{16±\sqrt{256-80}}{8}=\frac{16±\sqrt{179}}{8}\\ =\frac{16±\sqrt{16\times 11}}{8}\\ =\frac{16±4\sqrt{11}}{8}=\frac{4±\sqrt{11}}{2}=2±\frac{\sqrt{11}}{2}$

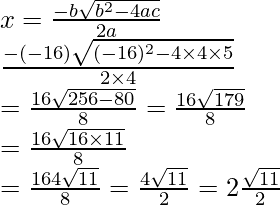
So, the co-ordinate of C will be (2 + √11/2, 5/2) or (2 – √11/2, 5/2)

问题16. x轴上的哪一点与(5，9)和(-4，6)等距?

解决方案：

Let co-ordinates of two points are A (5, 9), B (-4, 6)

The required point is on x-axis

Its ordinates or y-co-ordinates will be 0

Let the co-ordinates of the point C be (x, 0)

AC = CB

Now 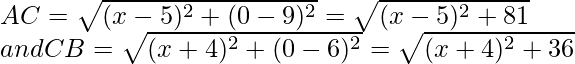$AC=\sqrt{(x-5)^2+(0-9)^2}=\sqrt{(x-5)^2+81}\\ and\space CB=\sqrt{(x+4)^2+(0-6)^2}=\sqrt{(x+4)^2+36}$

$\sqrt{(x-5)^2+81}=\sqrt{(x+4)^2+36}$

Squaring both sides, we get

(x – 5)² + 81 = (x + 4)² + 36

x² – 10x + 25 + 81 = x² + 8x + 16 + 36 – 10x – 8x

-18 = 52 – 106

-18x = -54

x = -54/18

x = 3

Hence, the required point is (3, 0)

问题17.证明点(-2，5)，(0，1)和(2，-3)是共线的。

解决方案：

Given points are A(-2, 5), B(0, 1) and C(2, -3)

Now we find the length of AB, BC, and CA

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(0+2)^2+(1-5)^2}\\ =\sqrt{(2)^2+(-4)^2}=\sqrt{4+16}\\ \sqrt{20}=\sqrt{4*5}=2\sqrt{5}\\BC=\sqrt{(2-0)^2+(-3-1)^2}\\ =\sqrt{(2)^2+(-4)^2}\\ =\sqrt{4+16}=\sqrt{20}=\sqrt{4*5}=2\sqrt{5}\\ CA=\sqrt{(-2-2)^2+(5+3)^2}\\ =\sqrt{(-4)^2+(8)^2}=\sqrt{16+64}\\ \sqrt{80}=\sqrt{16*5}=4\sqrt{5}$

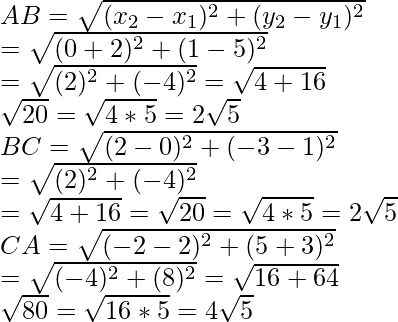
Now AB + BC = 2√5 + 2√5

And CA = 4√5

AB + BC = CA

Hence, A, B and C are collinear

问题18.点P的坐标是(-3，2)。找到位于连接P和原点的线上的点Q的坐标，使得OP = OQ。

解决方案：

Given that the co-ordinates of P are (-3, 2) and origin O are (0, 0)

Let us assume that the co-ordinates of Q be (x, y)

Here, O is the mid-point of line PQ

so by using mid point formula we get,

(x – 3)/2 = 0 and (y + 3)/2 = 0

x = 3, y = -2

Hence, the coordinates of the point Q are (3, -2)

问题19. y轴上的哪一点与(2，3)和(-4，1)等距?

解决方案：

The required point lies on y-axis

Its abscissa will be zero

So, let us assume that the point be C (0, y) and A (2, 3), B (-4, 1)

Now, we find the length of AC and BC

$AC=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(0-2)^2+(y-3)^2}\\ =\sqrt{(-2)^2+(y-3)^2}=\sqrt{4+(y-3)^2}\\BC=\sqrt{(0-4)^2+(y-1)^2}\\ =\sqrt{16+(y-1)^2}\\$

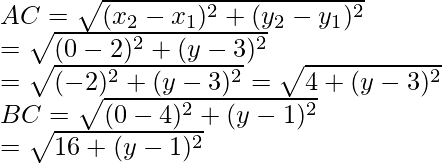
Here, we conclude that AC = BC

So, $\sqrt{4+(y-3)^2}=\sqrt{16+(y-1)^2}$

On squaring both sides, we get

4 + (y – 3)² = 16 + (y – 1)²

4 + y² + 9 – 6y = 16 + y² + 1 – 2y

-6y + 2y = 17 – 13

-4y = 4 = y = 4/-4 = 1

Hence, the coordinates of the required point is (0,-1)