问题1.假定下表为AP的第一项,d为共同差,第n为第n个项,请填写下表中的空白
| a | d | n | an | |
| I | 7 | 3 | 8 | – |
| II | -18 | – | 10 | 0 |
| III | – | -3 | 18 | -5 |
| IV | -18.9 | 2.5 | – | 3.6 |
| V | 3.5 | 0 | 105 | – |
解决方案:
(i) a = 7, d = 3, n = 8
Using A.P formula,
an = a + (n – 1)d
So, an = 7 + (8 – 1) * 3
an = 7 + 21
an = 28
(ii) a = -18, d = ?, n = 10, an = 0
Using A.P formula,
an = a + (n – 1)d
0 = -18 + (10 – 1) * d
18 = 9 * d
d = 2
(iii) a = ?, d = -3, n = 18, an = -5
Using A.P formula,
an = a + (n – 1)d
-5 = a + (18 – 1) * (-3)
-5 = a – 51
a = -5 + 51
a = 46
(iv) a = -18.9, d = 2.5, n = ?, an = 3.6
Using A.P formula,
an = a + (n – 1)d
3.6 = -18.9 + (n – 1) * 2.5
3.6 + 18.9 = (n – 1) * 2.5
n – 1 = 22.5/2.5
n – 1 = 9
n = 10
(v) a = 3.5, d = 0, n = 105, an = ?
Using A.P formula,
an = a + (n – 1)d
an = 3.5 + (105 – 1) * 0
an = 3.5
问题2.在下面选择正确的选择并证明
(i)AP的第30个任期:10、7、4,…是
(A)97(B)77(C)-77(D)-87
解决方案:
Given: A.P. is 10, 7, 4, ……
Now we find the common difference:
Common difference(d) = second term – first term
So, d = 7 -10 = -3
The first term (a) = 10
Total number of terms (n) = 30
Now, we find the 30th term
a30 (30th term) = a + (n – 1)d
a30 = 10 + (30 – 1) * (-3)
a30 = 10 – 87
a30 = -77
Hence, the correct option is C.
(ii)AP的第11任-3,-1 / 2、2……。是
(A)28(B)22(C)-38(D) 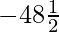
解决方案:
Given: A.P. is -3, -1/2, 2, …….
So, first term (a) = -3
Now, we find the common difference;
Common Difference (d) = second term – first term
d = -1/2 – (-3)
d = -1/2 + 3
d = 5/2
11th term can be calculated by following formula
an = a +(n – 1)d
a11 = -3 + (11 – 1) * (5/2)
= -3 + (10) * (5/2)
= -3 + 25
a11 = 22
Hence, option B is the correct choice.
问题3.在以下AP中,在框中找到缺少的术语
(i)2  ,26
,26
解决方案 :
Given: first term (a) = 2
third term (a3) = 26
a3 can be calculated using the formula an = a + (n – 1)d
a3 = 2 + (3 – 1) * d
26 = 2 + 2d
24 = 2d
d = 12
So a2 can be calculated using the formula an = a + (n – 1)d
a2 = 2 + (2 – 1) * 12
a2 = 2 + 12
a2 = 14
(ii)  ,13
,13  ,3
,3
解决方案:
Given:
a2 = 13
a + (2 – 1)d = 13
a + d = 13 -(1)
a4 = 3
a + (4 – 1)d = 3
a + 3d = 3 -(2)
After solving equation (1) and (2), you will get
d = -5
and a = 18
Now we find a3
a3 = 18 + (3 – 1) * (-5)
a3 = 18 -10
a3 = 8
Hence, the missing terms in the square boxes are 18 and 8.
(iii)5  ,
,  ,
, 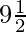
解决方案:
Given:
a = 5
a4 = 19/2
a + (4 – 1)d = 19/2
5 + 3d = 19/2
3d = (19/2) – 5
3d = 9/2
d = 9/6 = 3/2
So, a2 = 5 + (2 – 1) * (3/2)
a2 = 5 + 3/2
a2 = 13/2
and a3 = 5 + (3 – 1) * (3/2)
a3 = 5 + 3
a3 = 8
Hence, the missing terms in the square boxes are 13/2 and 8.
(iv)-4,  ,
,  ,
,  ,
,  ,6
,6
解决方案:
Given: a = -4
a6 = 6
a + (6 – 1)d = 6
-4 + 5d = 6
5d = 10
d = 2
So, a2 = a + d
a2 = -4 + 2 = -2
a3 = a + 2d
a3 = -4 + 4 = 0
a4 = a + 3d
a4 = -4 + 6 = 2
a5 = a + 4d
a5 = -4 + 8 = 4
Hence, the missing terms in the square boxes are -2, 0, 2, and 4.
(v)  ,38,
,38,  ,
,  ,
,  ,-22
,-22
解决方案:
Given:
a2 = 38
a + d = 38 -(1)
a6 = -22
a + 5d = -22 -(2)
After solving (1) and (2) equation, you will get
d = -15
and a= 53
So,
a3 = a + 2d
a3 = 53 – 30 = 23
a4 = a+ 3d
a4 = 53 – 45 = 8
a5 = a + 4d
a5 = 53 – 60 = -7
Hence, the missing terms in the square boxes are 53, 23, 8 and -7.
问题4. AP 3、8、13、18,……的哪个术语。是78吗?
解决方案:
Given:
a = 3
d = second term – first term
d = 8 – 3 = 5
and an = 78
n = ?
a + (n – 1)d = 78
3 + (n – 1) * 5 = 78
(n – 1) * 5 = 78 – 3
n – 1 = 75 /5
n = 15 +1
n = 16
So, 78 is the 16th term of the given A.P.
问题5.查找以下每个AP中的术语数
(i)7,13,19,……,205
解决方案:
Find: n = ?
Given: a = 7
d = 13 – 7 = 6
an = 205
a + (n – 1)d = 205
7 + (n – 1) * 6 = 205
(n – 1) * 6 = 205 – 7
n – 1 = 198/6
n = 33 + 1
n = 34
So, there are 34 terms in the given A.P.
(ii)18, 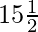 ,13,…….,-47
,13,…….,-47
解决方案:
Find: n = ?
Given: a = 18
d = 31/2 – 18 = -5/2
an = -47
18 + (n – 1) * (-5/2) = -47
(n – 1) * (-5/2) = -47 – 18
n – 1 = -65 * (-2/5)
n – 1 = 130/5
n = 26 + 1
n = 27
Hence, there are 27 terms in the given A.P.
问题6.检查-150是否为AP 11、8、5、2,……的术语。
解决方案:
Given:
a = 11
d = 8 – 11 = -3
Suppose -150 is the nth term of the given A.P. then it can be written as
a + (n – 1)d = -150
11 + (n – 1) * (-3) =- 150
(n – 1) * (-3) = -150 – 11
n – 1 = -161/(-3)
n = 161/3 + 1
n = 164/3
As you can see that n is not in integer. Hence, -150 is not a term in the given A.P.
问题7.找出AP的第31项,其第11项为38,第16项为73。
解决方案:
Given:
a11 = 38
a + 10 * d = 38 -(1)
a16 = 73
a + 15 * d = 73 -(2)
Subtracting equation (1) from equation (2), you will get
15 * d – 10 * d = 73 – 38
d = 35/5
d = 7
After putting value of d in equation (1) you will the value of a
a = 38 – 70
a = -32
So, a31 = a + (31 – 1) * d
a31 = -32 + 30 * 7
a31 = 178
Hence, 31st term of the given A.P. is 178.
问题8.在AP中包含50个术语,其中第三个术语是12,最后一个术语是106。找到第29个术语。
解决方案:
According to the question:
n = 50
a3 = 12
a + 2 * d = 12 -(1)
a50 = 106
a + 49 * d = 106 -(2)
After solving (1) and (2) you will get
47 * d = 106 – 12
d = 94/47 = 2
and a = 12 -4 = 8
So, a29 = a + 28 * d
a29 = 8 + 28 * 2
a29 = 64
So the 29th term of the given A.P. will be 64.
问题9. AP的第3和第9项分别是4和-8。该AP的哪个项为零?
解决方案:
Given: a3 = 4
a + 2 * d = 4 -(1)
and a9 = -8
a + 8 * d = -8 -(2)
After solving (1) and (2), you will get
d = -2
and a = 8
Let the nth term of the A.P. will be zero.
So an = 0
a + (n – 1)d = 0
8 + (n – 1) * (-2) = 0
n – 1 = -8/(-2)
n = 4 + 1
n = 5
Hence, the 5th term of the given A.P. will be zero.
问题10.如果AP的第17项比其第10项多7。找到共同点。
解决方案:
According to the question
a17 = a10 + 7
a + (17 – 1)d = a + (10 – 1)d + 7
16 * d = 9 * d + 7
7 * d = 7
d = 1
Hence, the common difference of the given A.P. will be 1.
问题11. AP 3、15、27、39,……的哪个任期比其第54个任期多132个?
解决方案:
According to the question
d = 15 – 3 = 12
Let the nth term of the A.P. will be 132 more than its 54th term
an = a54 + 132
a + (n – 1)d = a + (54 – 1)d + 132
(n – 1)(12) = 53 * 12 + 132
(n – 1) * 12 = 636 + 132
n – 1 = 771 / 12
n = 64 + 1
n = 65
Hence, 65th term will be 132 more than its 54th term.
问题12.两个接入点具有相同的共同点。他们的第100个学期的差是100,他们的第1000个学期的差是多少?
解决方案:
Let d be common difference of both APs and a1 be the first term of
one A.P. and a2 be the first term of other A.P.
So, a100 for first A.P. will be
a100 = a1 + 99d
and a100 for second A.P. will be
a100 = a2 + 99d
According to the question, the difference between their 100th term is 100
So, (a1 + 99d) – (a2 + 99d) = 100
a1 – a2 = 100 -(1)
Now a100 for first A.P. will be
a1000 = a1 + 999d
and a1000 for second A.P. will be
a1000 = a2 + 999d
Difference between their 1000th term will be
= (a1 + 999d) – (a2 + 999d)
= a1 – a2
= 100 -(from (1) a1 -a2 = 100)
Hence, the difference between their 1000th term will be 100.
问题13.多少个三位数可以被7整除?
解决方案:
First three-digit number that is divisible by 7 = 105
So, the first term of the AP (a) = 105
and common difference (d) = 7
The last three-digit number that is divisible by 7 = 994
So AP will look like 105, 112, 119,………, 994
Let there are n three-digit numbers between 105 and 994
You have an = 994
a + (n – 1)d = 994
105 + (n – 1) * 7 = 994
(n – 1) * 7 = 994 – 105
n – 1 = 889/7
n = 127 + 1
n = 128
Hence, there 128 three-digit numbers that are divisible by 7.
问题14. 4的多少个倍数在10到250之间?
解决方案:
Given:
12 is the minimum number that is divisible by 4 between 10 and 250.
So, a = 12
d = 4
248 is the highest number that is divisible by 4 between 10 and 250.
So an = 248
a + (n – 1)d = 248
12 + (n – 1) * 4 = 248
(n – 1) * 4 = 236
n – 1 = 59
n = 60
Hence, there are 60 multiples of 4 between 10 and 250.
问题15:对于两个AP 63、65、67 …的n个项,n的值是多少?和3,10,17,…..相等吗?
解决方案:
For A.P. 63, 65, 67,…..
a = 63 and d = 65 – 63 = 2
nth term for this AP will be
an = 63 + (n – 1) * 2
For A.P. 3, 10, 17, ….
a = 3 and d = 10 – 3 = 7
nth term for this AP will be
an = 3 + (n – 1) * 7
According to the question, nth terms of both APs are equal
So, 63 + (n – 1) * 2 = 3 + (n – 1) * 7
60 = (n – 1) * 5
n – 1 = 12
n =13
Hence, 13th of both the APs are equal.
问题16。确定AP的第三项为16,第七项比第五项高12。
解决方案:
a3 = 16
a + 2d = 16 -(1)
and a7 = a5 + 12
a + 6d = a + 4d + 12
2d = 12
d = 6
On putting value of d in equation (1), you will get
a = 16 – 12
a = 4
So, AP will look like, 4, 10, 16, 22, 28,…..
问题17.从AP 3的上学期中找到第20个学期,即8、13,…………,253
解决方案:
d = 8 – 3 = 5
In reverse order the AP will be
253, 248, ………. 13, 8, 3
Now for this AP
a = 253 and d = 248 – 253 = -5
So 20th term will be
a20 = a + 19d
a20 = 253 + 19 * (-5)
a20 = 158
Hence, the 20th term from the last term for the given AP will be 158.
问题18. AP的第4和第8项的总和为24,第6和第10项的总和为44。找到AP的前三项。
解决方案:
Given: a4 + a8 = 24
a + 3d + a + 7d = 24
2a + 10d = 24
a + 5d = 12 -(1)
and a6 + a10 = 44
a + 5d + a + 9d = 44
2a + 14d = 44
a + 7d = 22 -(2)
From (1) and (2), you will get
d = 5
and a = -13
So a2 = a + d
a2 = -13 + 5 = -8
a3 = a + 2d
a3 = -13 + 10 = -3
Hence, the first three terms of the AP are -13, -8, -3
问题19. Subba Rao于1995年开始工作,年薪为5000卢比,每年增加200卢比。在哪一年他的收入达到了7000卢比。
解决方案:
As, salary of Subba Rao is increasing by a fixed amount in every year hence
this will form an AP with first term (a) = 5000 and common difference (d) d = 200
an = 7000
a +(n – 1)d = 7000
5000 + (n – 1) * 200 = 7000
n – 1 = 2000/200
n = 10 + 1
n = 11
Hence, the salary will be 7000 in 11th year.
问题20. Ramkali在一年的第一周节省了5卢比,然后每周增加了1.75卢比的储蓄。如果在第n周她的每周储蓄变成20.75卢比,请找到n。
解决方案:
As saving is increased by a fixed amount, this will form an AP in which
First term (a) = 5
Common difference (d) = 1.75
an = 20.75
a + (n – 1)d = 20.75
5 + (n – 1) * (1.75) = 20.75
(n – 1) * (1.75) = 20.75 – 5
n – 1 = 15.75/1.75
n = 9 + 1
n = 10
Hence, n = 10