问题11。在下图中,E是等腰三角形ABC(AB = AC)在CB边上的一点。如果AD⊥BC和EF⊥AC,则证明ΔABD〜ΔECF。

解决方案:
Given, ABC is an isosceles triangle.
Since, the sides of an isosceles triangle are equal, we have,
∴ AB = AC
⇒ ∠ABD = ∠ECF
In ΔABD and ΔECF,
Since, each of the following angles are 90°.
∠ADB = ∠EFC
Since, we have already proved,
∠BAD = ∠CEF
By AA similarity criterion, we have,
∴ ΔABD ~ ΔECF
问题12.三角形ABC的AB边和BC边以及中值AD分别与ΔPQR的PQ和QR边和PM中值成正比(见图6.41)。表示ΔABC〜ΔPQR。

解决方案:
Given that in ΔABC and ΔPQR,
AB is proportional to PQ
BC is proportional to QR
AD is proportional to PM
That is, AB/PQ = BC/QR = AD/PM
We know,
AB/PQ = BC/QR = AD/PM
Since, D is the midpoint of BC and M is the midpoint of QR
⇒AB/PQ = BC/QR = AD/PM
By SSS similarity criterion, we have,
⇒ ΔABD ~ ΔPQM
Now, since the corresponding angles of two similar triangles are equal, we obtain,
∴ ∠ABD = ∠PQM
⇒ ∠ABC = ∠PQR
Now,
In ΔABC and ΔPQR
AB/PQ = BC/QR ………….(i)
∠ABC = ∠PQR ……………(ii)
From equation (i) and (ii), we get,
By SAS similarity criterion, we have,
ΔABC ~ ΔPQR
问题13. D是三角形ABC的边BC上的一点,使得∠ADC=∠BAC。证明CA2 = CB.CD
解决方案:
Given, D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC.

In ΔADC and ΔBAC,
∠ADC = ∠BAC
∠ACD = ∠BCA (Common angles)
By AA similarity criterion, we have,
∴ ΔADC ~ ΔBAC
Since, the corresponding sides of similar triangles are in proportion, we obtain,
∴ CA/CB = CD/CA
That is, CA2 = CB.CD.
Hence, proved.
问题14.三角形ABC的边AB和AC和中值AD分别与另一个三角形PQR的边PQ和PR和中值PM成比例。表示ΔABC〜ΔPQR。
解决方案:
Given, Two triangles ΔABC and ΔPQR in which AD and PM are medians such that;
Now,
AB/PQ = AC/PR = AD/PM
Construction,
Produce AD further to E so that AD = DE. Now, join CE.
Similarly, produce PM further until N such that PM = MN. Join RN.

In ΔABD and ΔCDE, we have
From the construction done,
AD = DE
Now, since AP is the median,
BD = DC
and, ∠ADB = ∠CDE [Vertically opposite angles are equal]
By SAS criterion,
∴ ΔABD ≅ ΔCDE
By CPCT, we have,
⇒ AB = CE……………..(i)
In ΔPQM and ΔMNR,
From the construction done,
PM = MN
Now, since PM is the median,
QM = MR
and, ∠PMQ = ∠NMR [Vertically opposite angles are equal]
By SAS criterion,
∴ ΔPQM = ΔMNR
By CPCT,
⇒ PQ = RN …………………(ii)
Now, AB/PQ = AC/PR = AD/PM
From equation (i) and (ii), we conclude,
⇒CE/RN = AC/PR = AD/PM
⇒ CE/RN = AC/PR = 2AD/2PM
We know,
2AD = AE and 2PM = PN.
⇒ CE/RN = AC/PR = AE/PN
By SSS similarity criterion,
∴ ΔACE ~ ΔPRN
Thus,
∠2 = ∠4
And, ∠1 = ∠3
∴ ∠1 + ∠2 = ∠3 + ∠4
⇒ ∠A = ∠P ………………….(iii)
Now, in ΔABC and ΔPQR, we have
AB/PQ = AC/PR [Given]
From equation (iii), we have,
∠A = ∠P
By SAS similarity criterion,
∴ ΔABC ~ ΔPQR
问题15.一根长6 m的垂直杆在地面上投下4m长的阴影,同时,一塔在投下28 m长的阴影。找到塔的高度。
解决方案:
Given, Length of the vertical pole = 6m
Length of shadow of the tower = 28 m

Shadow of the pole = 4 m
Let us assume the height of tower to be h m.
In ΔABC and ΔDEF,
∠C = ∠E (By angular elevation of sum)
Since, the following angles are equivalent to 90°
∠B = ∠F
By AA similarity criterion, we have,
∴ ΔABC ~ ΔDEF
Since, if two triangles are similar corresponding sides are proportional
∴ AB/DF = BC/EF
Substituting values,
∴ 6/h = 4/28
⇒h = (6×28)/4
⇒ h = 6 × 7
⇒ h = 42 m
Hence, the height of the tower specified is 42 m.
问题16:如果AD和PM分别是三角形ABC和PQR的中值,则ΔABC〜ΔPQR证明AB / PQ = AD / PM。
解决方案:
Given, ΔABC ~ ΔPQR
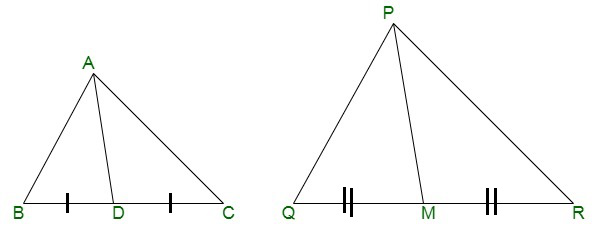
Since, the corresponding sides of similar triangles are in proportion.
∴ AB/PQ = AC/PR = BC/QR……………(i)
And, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ………….…..(ii)
Since, AD and PM are the medians, they will divide their opposite sides correspondingly.
∴ BD = BC/2 and QM = QR/2 ………….(iii)
From equations (i) and (iii), we obtain,
AB/PQ = BD/QM …………….(iv)
In ΔABD and ΔPQM,
From equation (ii), we have
∠B = ∠Q
From equation (iv), we have,
AB/PQ = BD/QM
By SAS similarity criterion, we have,
∴ ΔABD ~ ΔPQM
That is, AB/PQ = BD/QM = AD/PM