11类RD Sharma解决方案–第3章功能–练习3.1 |套装2

问题10.如果f，g，h是从R到R定义的三个函数，如下所示：

(i)f(x)= x ²

(ii)g(x)= sinx

(iii)h(x)= x ² +1

找到每个函数的范围。

解决方案：

(i) We have,

f(x) = x²

Range of f(x) = R+ (set of all real numbers greater than or equal to zero)

= {x ∈ R+ | x ≥ 0}

(ii) We have

g(x) = sinx

Range of g(x) = {x ∈ R : -1 ≤ x ≤ 1}

(iii) We have

h(x) = x² + 1

Range of h(x) = {x ∈ R : x ≥ 1}

问题11。设X = {1,2,3,4}，Y = {1,2,5,9,11,15,16}

确定以下哪些集合是从X到Y的函数

(a)f ₁ = {(1，1)，(2，11)，(3，1)，(4，15)}

(b)f = {(1，1)，(2，7)，(3，5)}

(c)f = {(1,5)，(2、9)，(3、1)，(4、5)，(2、11)}

解决方案：

(a) We have,

f₁ = {(1, 1), (2, 11), (3, 1), (4, 15)}

f₁ is a function from X to Y

(b) We have,

f₂ = {(1, 1), (2, 7), (3, 5)}

f₂ is not a function from X to Y because there is an element 4 ∈ x  which is not associated to any element of Y.

(c) We have,

f₃ = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

f₃ is not a function from X to Y because an element 2 ∈ x is associated to two elements 9 and 11 in Y.

问题12。令A = {12、13、14、15、16、17}和f：A Z是由f(x)= x的最高素因数给定的函数。查找f的范围。

解决方案：

We have,

f(x) = highest prime factor of x.

Therefore,

12 = 3 × 4,

13 = 13 × 1,

14 = 7 × 2,

15 = 5 × 3,

16 = 2 × 8,

17 = 17 × 1

Therefore,

f = {(12, 3), (13, 3), (14, 7), (15, 5), (16, 2), (17, 17)}

Range (f) = {3, 13, 7, 5, 2, 17}

问题13：如果f：R⇢R由f(x)= x ² +1定义，则求出f ^-1 {17}和f ^-1 {-3}。

解决方案：

We know that,

if f : A ⇢ 13

such that y ∈ 3. Then,

f^-1 (y) = {x ∈ A : f(x) = y}. In other words, f^-1 (y) is the set of pre-images of y.

Let f^-1 (17) = x. Then, f(x) = 17

⇒ x² + 1 = 17

⇒ x² = 17 – 1 = 16

⇒ x = ±4

Let f^-1 {-3} = x. Then, f(x) = -3

⇒ x² + 1 = -3

⇒ x² = -3 – 1 = -4

⇒ x = $\sqrt{-4}$

Therefore, f-1 {-3} = 0

问题14.设A = {p，q，r，s}，B = {1,2,3}。从A到B的以下哪个关系不是函数?

(a)R ₁ = R ₁ = {(p，1)，(q，2)，(r，1)，(s，2)}

(b)R ₂ = {(p，1)，(q，1)，(r，1)，(s，2)}

(c)R ₃ = {(p，1)，(q，2)，(p，2)，(s，3)}

(d)R ₄ = {(p，2)，(q，3)，(r，2)，(s，2)}

解决方案：

We have

A = {p, q, r, s} and B = {1, 2, 3}

(a) Now,

R₁ = {(p, 1), (q, 2), (r, 1), (s, 2)}

R₁ is a function

(b) Now,

R₂ = {(p, 1), (q, 2), (r, 1), (s, 1)}

R₂ is a function

(c) Now,

R₃ = {(p, 2), (q, 3), (r, 2), (s, 2)}

R₃ is not a function because an element p ∈ A is associated to two elements 1 and 2 in B.

(d) Now,

R₄ = {(p, 2), (q, 3), (r, 2), (s, 2)}

R₄ is a function

问题15。设A = {9,10,11,12,13}，设f：A⇢N由f(n)= n的最高质因数定义。找出f的范围。

解决方案：

We have,

f(n) = the highest prime factor of n.

Now,

9 = 3 × 3,

10 = 5 × 2,

11 = 11 × 1,

12 = 3 × 4,

13 = 13 × 1

Therefore,

f = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13)}

Clearly, range(f) = {3, 5, 11, 13}

问题16.函数f由下定义

$f(x)=\begin{cases}x^2,\ 0\le x\le 3\\ 3x,\ 3\le x\le 10\end{cases}$

关系f定义为

$g(x)=\begin{cases}x^2,\ 0\le x\le 2\\ 3x,\ 2\le x\le 10\end{cases}$

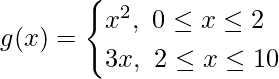
证明f是一个函数而g不是一个函数

解决方案：

We have,

$f(x)=\begin{cases}x^2,\ 0\le x\le 3\\ 3x,\ 3\le x\le 10\end{cases}$

and, 

$g(x)=\begin{cases}x^2,\ 0\le x\le 2\\ 3x,\ 2\le x\le 10\end{cases}$

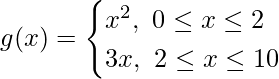
Now, f(3) = (3)² = 9 and f(3) = 3 × 3 = 9

and, g(2) = (2)² = 4 and g(2) = 3 × 2 = 6

We observe that f(x) takes unique value at each point in its domain [0,10]. However, g(x) does not take unique value at each point in its domain [0, 10].

Hence, g(x) is not a function.

问题17.如果f(x)= x ² ，则找到

$\frac{f(1.1)-f(1)}{(1.1)-1}$

解决方案：

Given f(x) = x²

f(1.1) = 1.21

f(1) = 1

$\frac{f(1.1)-f(1)}{(1.1)-1}=\frac{1.21-1}{1.1-1}\\ =\frac{0.21}{0.1}$

= 2.1

问题18：将函数f表示为：f(x)= x ³ +1作为有序对集合，其中x = {-1，0，3，9，7}。

解决方案：

f : X ⇢ R given by f(x) = x³ + 1

f(-1) = (-1)³ + 1 = -1 + 1 = 0

f(0) = (0)³ + 1 = 0 + 1 = 1

f(3) = (3)³ + 1 = 27 + 1 = 28

f(9) = (9)³ + 1 = 81 + 1 = 82

f(7) = (7)³ + 1 = 343 + 1 = 344

Set of ordered pairs are {(-1, 0), (0, 1), (3, 28), (9, 82), (7, 344)}