直线可以看作是在任意两个相反方向上无限延伸的点。一条直线是没有曲线并且覆盖无限数量的点的直线。

直线的性质
- 无限数量的直线穿过一个点
- 无限数量的平面包含一条直线(在3维视图中查看)
- 一条直线具有无限个点
- 连接直线上任意两点的线段位于该直线上
基本术语
- 点:点是具有位置的无量纲几何图形(相对于某些参考,例如:坐标系中的点)。
- 平面:无限区域的平面。它是二维的。
- 射线:当点在平面中的任何一个方向上无限延伸时,会形成射线。

- 线段:连接两个点的最短曲线称为线段。

在2-D和3-D中研究直线。我们将讨论二维的直线,为此,我们使用坐标系。
坐标轴
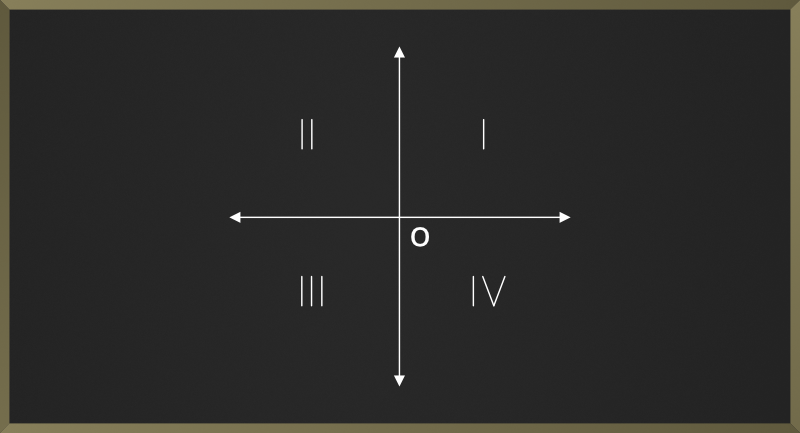
两条垂直线将平面(我们考虑在内)分为4个区域,称为象限。
令AB为该平面上的直线。令线AB与X轴之间的角度为w°。然后,AB行可以是:
- 与X轴平行,w = 0°
- 与Y轴平行,w = 90°
- 与X轴成w°角(参见下图),0°

直线斜率
定义为直线和X轴之间的角度(此处为tan(w))的正切值,如下所示:
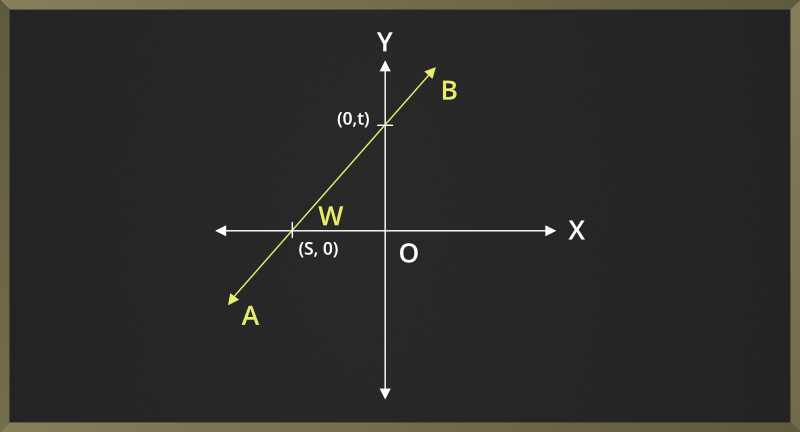
slope of line AB
= tan(w)
= (0 – t) / (s – 0)
= t/s
也就是说,如果(x 1 ,y 1 )和(x 2 ,y 2 )是AB线上的两个点,
slope of line AB
= tan(w)
= (y2 – y1) / (x2 – x1)
= (y1 – y2) / (x1 – x2)
= distance between the y coordinate of both points / distance between the x coordinate of both points
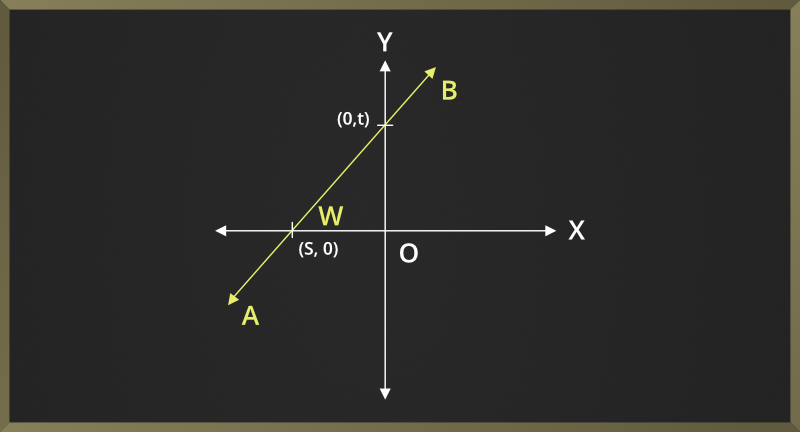
X截距
线与x轴的交点称为x截距。
示例:这里,s是线AB的x截距
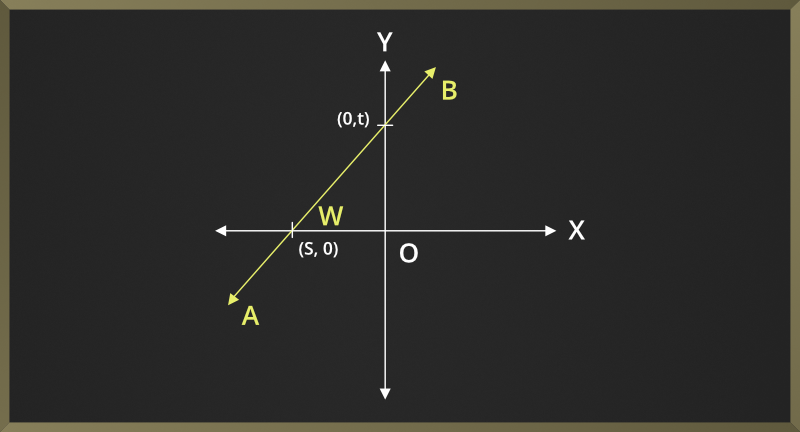
Y轴截距
线与y轴的交点称为y截距。
示例:这里,t是线AB的y截距
直线方程
直线可以以多种形式表示:
- 截距形式
- 点坡形式
- 两点式等
我们将牢记上述数字来讨论(i)截距。
斜率截距形式的直线方程为:
y = slope * x + c
y = tan(w) * x + c
y = mx + c
Here m = tan(w) = slope of line AB and c is the y-intercept.
直线上的样本问题
现在,我们可以轻松地执行以下任务:
问题1:写一条直线方程,其斜率为p,y轴截距为g。
Solution: y = p * x + g
问题2:写一条直线方程,其斜率为1/2,y轴截距为11。
Solution: y = (1/2) * x + 11
问题3:写一条通过原点且斜率为1/6的直线方程。
Solution:
Since the line passes through the origin,
Y-intercept = 0
y = (1/6) * x + 0
y = (1/6)x,
which is the required equation.
问题4:找到方程y = tx + 4表示的直线的斜率和y轴截距
Solution:
The equation of the given line is in slope-intercept form.
Thus, slope of the given line is t and its y-intercept is 4.
问题5:找到方程y + 4 = x表示的直线的斜率和y轴截距
Solution:
The given equation is not in slope-intercept form.
Therefore, we convert it to that form.
y = x – 4
y = 1 * x – 4
Thus, slope of the given line is 1 and its y-intercept is -4.
问题6:找到方程x = y / q表示的直线的斜率和y轴截距
Solution:
The given equation is not in slope-intercept form.
Therefore, we convert it to that form.
y = qx
y = qx + 0
Thus, slope of the given line is q and its y-intercept is 0.
问题7:求等式x = d表示的直线的斜率和y轴截距
Solution:
The given equation is not in slope-intercept form.
Moreover, the variable y is not present in the equation i.e. the equation of this line is independent of the value of variable y.
Equations like this represent lines which are parallel to y-axis.
For lines that are parallel to y-axis w = 90°,
thus the slope of these lines is not defined because tan(90°) is not defined.
Since, the line is parallel to y-axis, it never intersects the y-axis and hence does not have y-intercept.
问题8:找到方程y = h表示的直线的斜率和y轴截距
Solution:
The given equation is not in slope-intercept form.
Moreover, the variable x is not present in the equation i.e.
the equation of this line is independent of the value of variable x.
Equations like this represent lines which are parallel to x-axis.
Given equation can be rewritten as:
y = 0x + h,
which is the slope intercept form of the given line.
Thus, slope of given line is 0 and its y-intercept is h.
样词问题
问题1:出租车的前2公里的基本票价是30.00卢比。之后,向骑行者收取每公里4卢比的费用。通过形成一个线性方程,计算出行驶14 km所需的车费。
解决方案:
Base fare = Rs 30, this means that Rs 30 is the minimum fare.
Therefore, the fare for the distances from 1m to 2000m (2km) is Rs 30.
Fare for distances after 2 km is Rs. 4/km.
Let the total distance traveled be d km and total cost be Rs c.
Charge up to the first 2 km charge is Rs 30.00.
Charge for the rest of the (d-2) km charge is Rs 4 * (d – 2).
Therefore, total fare is given by the equation,
c = 4 * (d – 2) + 30
c = 4 * d – 8 + 30
c = 4 * d + 22,
(which is of the slope intercept form)
Given, d = 14km,
Therefore, total cost,
c = 4 * 14 + 22
= 56 + 22
= 78
Thus, the fare for travelling the distance of 14km is Rs 78.
问题2:出租车的前2公里的基本票价是30.00卢比。之后,向骑手收取每600m Rs 4的费用。通过形成一个线性方程,计算出行驶14 km所需的车费。
解决方案:
Base fare = Rs 30, this means that Rs 30 is the minimum fare.
Therefore, the fare for the distances 1m to 2000m (2km) is Rs 30.
Fare for distances after 2 km is Rs4 per 600m.
Let the total distance traveled be d km and total cost be Rs c.
Up to the first 2 km charge is Rs 30.00.
Remaining distance = (d – 2)km
Charge for 600 m = Rs 4
Charge for 1 m = Rs (4/600) ———(unitary method)
Charge for 1000m = Rs. (4 / 600) * 1000 = Rs (40/6)
Therefore, the charge per km after the first 2 km is Rs (40/6) per km.
Charge for the rest of the (d – 2) km is Rs (40/6) * (d – 2).
Therefore, total fare is given by the equation,
c = (40/6) * (d – 2) + 30
c = (40/6) * d – 20/6 + 30
c = (20/3) * d + (-20 + 180) / 6
c = (20/3) * d + (160/6)
c = (20/3) * d + (80/3),
(which is of the slope-intercept form)
Given, d = 14km,
Therefore, total cost,
c = (20/3) * 14 + (80/3)
= (280/3) + (80/3)
= 360/3
= 120 (approx.)
Thus, the total fare for traveling the distance of 14km is Rs 120 (approximately).
问题3:地球航空拥有的13号飞机正在维修中。工程师被告知,在维修之前,航空公司每12分钟可能遭受1300卢比的损失。工程师被告知,航空公司所遭受的损失不会超过5000卢比,并且多余的金额将从他的薪水中扣除。计算
- 工程师必须维修的最长时间(以分钟为单位)。
- 如果总损失为6000卢比,则花费的总时间
解决方案:
Loss in 12 min = Rs. 1300
Loss in 1 min = Rs. (1300/12) = Rs. (325/3)
Therefore, loss per minute is Rs. (325/3).
(i)
Let the maximum time be t minutes.
Therefore, t * (325/3) = 5000
or t = (5000 * 3)/325
or t = 46.15 minutes = 46 minutes (approx.)
Thus, the engineer has to repair the airplane within 46 minutes.
(ii)
Total loss = Rs 6000 (Given)
Let the time taken for this loss be k minutes.
Time required for loss of Rs(325/3) = 1 min (unitary method)
Time required for loss of Rs 1 = 1 * (3/325)min
Therefore, time required for loss of Rs 6000 = 6000 * (3/325) minutes = 55.384 minutes
问题4:X和y是两个2位数字,它们满足以下条件:
- y> x
- x + y = m,其中m是通过反转y的位数获得的2位数
- y – x = x – 1
- y的十位数– y的位数= -2
找到两个数字。
解决方案:
y – x = x – 1, ——-condition(iii) can be rewritten as
y = x + x – 1
y = 2x – 1 ———-(1)
Let the tens and units digits of the number y be a and b respectively.
This means that y = 10a + b
and m = 10b + a
From condition(ii),
x + y = m
x + 10a + b = 10b + a
9a – 9b + x = 0
9(a – b) + x = 0
9 * (-2) + x = 0, ——-condition (iv)
-18 + x = 0
Therefore, x = 18
Substituting the value of x in equation (1),
y = 2 * 18 – 1
y = 36 – 1
Therefore, y = 35
问题5:在一个主题中,两个朋友的分数之和为100。在同一主题中,两个朋友的分数之差为10。找到他们的分数。
解决方案:
Let the scores be x and y such that x > y.
Given, x + y = 100 —-(1)
and x – y = 10 —-(2)
Adding equations (1) and (2),
x + y + x – y = 100 + 10
2x + 0y = 110
2x = 110
x = 110/2 = 55
Substituting value of x in equation (2)
55 – y = 10
55 – 10 = y
y = 45
Therefore, their scores are 45 and 55.