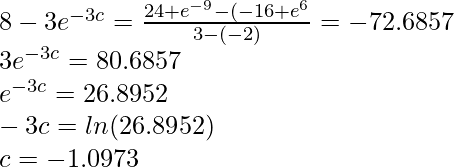平均值定理(MVT)是数学教育文献中经常出现的定理之一。它是用来证明微分和积分微积分中许多其他定理的最重要工具之一。有时以特殊情况(罗尔定理)进行讲授。罗尔定理以法国数学家米歇尔·罗尔(Michel Rolle(1652-1719))的名字命名,他建立了现在第n个根的通用符号,并坚持认为-a> -b对于正a和b,a 它声明如果y = f(x)并给出间隔[a,b],并且它满足以下条件: 然后,至少存在一个实数c∈(a,b),使得f’(c)= 0。 Note: It is not necessary that the converse of this theorem is also true. That is we cannot say if at some point f'(c) = 0 then all the conditions of Rolle’s theorem are satisfied. Let k = f(a) = f(b). We consider three cases: Case 1: If f(x) = k for all x ∈ (a, b), then f'(x) = 0 for all x ∈ (a, b). Case 2: Since f is a continuous function over the closed, bounded interval[a, b], by the extreme value theorem, it has an absolute maximum. Also, since there is a point x ∈ (a, b) such that f(x) > k, the absolute maximum is greater than k. Therefore, the absolute maximum does not occur at either endpoint. As a result, the absolute maximum must occur at an interior point xc∈ (a, b). Because f has a maximum at an interior point c, and f is differentiable at c, by Fermat’s theorem, f'(c)=0. Case 3: The case when there exists a point x ∈ (a, b) such that f(x) < k is analogous to case 2, with maximum replaced by minimum. 问题1:确定在[-1,3]上满足f(x)= x 2 – 2x – 8的Rolle定理的所有点’c’。 解决方案: Before finding out the points, we need to make sure that all the conditions of rolle’s theorem are applied on this interval. This function is a polynomial, so it’s both differentiable and continuous on the interval. Now let’s evaluate the function at the ends of the interval. f(-1) = -5 and f(3) = -5. Function values are equal at both the ends. So, now all the conditions for rolle’s theorem are satisfied. f'(x) = 2x – 2. f'(x) = 2x – 2 = 0. = x = 1 So, c = 1. 问题2:确定在区间[-2,1]上满足f(x)= 2x- x 2 – x 3的rolle定理的所有点“ c”。 解决方案: This function is also a polynomial, so it is both differential and continuous on the interval. Values at the end of the interval f(-2) = 0 = f(1). So, Rolle’s theorem is applicable here. f'(x) = 2 – 2x – 3x2 For finding the points like ‘c’ f'(x) = 0 ⇒ 2 – 2x – 3x2 = 0 ⇒ 3x2 + 2x -2 = 0 Applying the Shree Dharacharya quadratic formula for finding the values of c, So, here there are two values which satisfy rolle’s theorem. 问题3:检查x∈[5,9]的rolle定理是否适用于函数f(x)= [x]。 解决方案: This function is a step function, it is not continous. So, rolle’s theorem is not applicable in the following interval. f(x) = [x] 它是微积分中最重要的定理之一。它声明如果y = f(x)并给出间隔[a,b],并且它满足以下条件: 然后至少存在一个数c∈(a,b)使得 从几何学上讲,在c处的导数表示f(x)在x = c处的切线的斜率。它说,在该间隔之间必须存在一个点,其中切线的斜率等于连接点x = a和x = b的线的斜率。 Note: There can be any number of c-points. The mean Value Theorem is also called First Mean Value Theorem. 证明: Let “f” satisfy the hypotheses of the MVT on the interval [a, b]. Define Case 1: g attains its maximum and minimum at a and b. Then “g” is constant. In this case we get Case 2: If the maximum or the minimum is attained at an interior point c, then g'(c)=0. Therefore, 众所周知,在中值定理中, 均值定理是分析中最重要的定理之一,因此,其所有应用都具有重要意义。下面列出了一些应用程序: 问题1:确定满足[2,5]上h(z)= 4z 3 – 8z 2 + 7z – 2的均值定理结论的所有数字“ c”。 解决方案: Since the function is a polynomial, so it is continuous and differentiable both in this interval. Thus mean value theorem can be applied here. h(2) = 12 and h(5) = 333 and h'(z) = 12z2 -16z + 7 Now plug this into the formula of mean value theorem and solve for c. 问题2:f(x)= 解决方案: f(x) is not defined at x = 0. So, x = 0 is not in the domain if f(x). Since MVT can only be defined at places where f(x) is differentiable and continuous. It can be defined (-∞, 0) and (0,∞). 问题3:确定在区间[-2,2]中对于f(x)=满足均值定理结论的所有数字“ c” 解决方案: The given function, f(x) = |x – 2| + |x| is not differentiable. Thus mean value theorem cannot be applied on this function in the interval [-2, 2]. Graph of the given function. 问题4:确定满足以下条件的均值定理结论的所有数字“ c” 解决方案: This function is a sum of both exponential and polynomial functions. Since both the functions are continuous and differentiable everywhere, the function f(t) is continuous and differentiable everywhere. Thus mean value theorem is applicable. f(-2) = -16 + e(-3 .-2) = -16 + e6, f(3) = 24 + e-9 and f'(t) = 8 -3e-3t. Let’s plug it into the formula, This is the value of c. 罗尔定理
罗尔定理的证明
样本问题
![]()
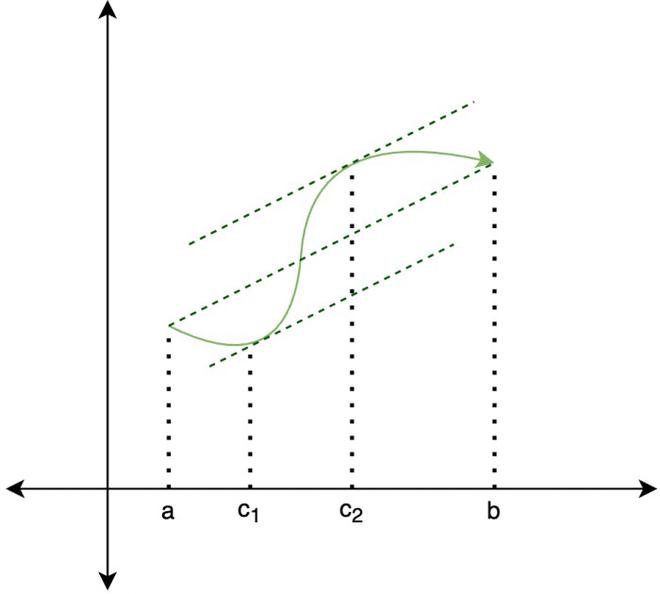
均值定理
![]()
![]() . This represents the secant line between a and b.
. This represents the secant line between a and b. ![]() at every point in [a, b]
at every point in [a, b]![]()
中值定理的物理解释
![]() 是[a,b]上函数的平均变化,而f’(c)是’c’处的瞬时变化。它指出在间隔内瞬时变化等于某个内部点处函数的平均变化。
是[a,b]上函数的平均变化,而f’(c)是’c’处的瞬时变化。它指出在间隔内瞬时变化等于某个内部点处函数的平均变化。中值定理的应用
![]() R是可微的,对于所有x \ in(a,b),f’(x)= 0。
R是可微的,对于所有x \ in(a,b),f’(x)= 0。样本问题
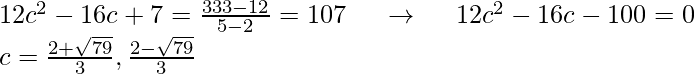
![]() 。找到可以应用平均值定理的时间间隔。
。找到可以应用平均值定理的时间间隔。![]()
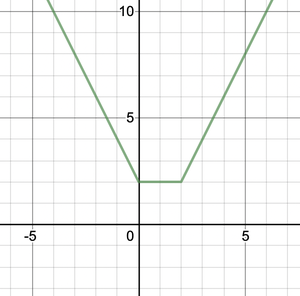
![]() 在[-2,3]上。
在[-2,3]上。