问题1.令f:{1,3,4}-> {1,2,5}和g:{1,2,5}-> {1,3}由f = {(1,2) ,(3、5),(4、1)和g = {(1、3),(2、5),(5、1)}。写下gof。
解决方案:
f= {(1, 2), (3, 5), (4, 1)}
g= {(1, 3), (2, 3), (5, 1)}
f(1)= 2, g(2) = 3 => gof(1) = 3
f(3) = 5, g(5) = 1 => gof(3) = 1
f(4) =1, g(1) = 3 => gof(4) = 3
=> gof = {(1,3), (3,1), (4,3)}
问题2。令f,g和h为从R到R的函数。证明(f + g)oh = foh + goh,(f * g)oh =(foh)*(goh)。
解决方案:
f: R-> R, g: R-> R, h: R-> R
(f+g) oh(x) = (f+g) oh(x)
= (f+g) [h(x)]
= f[h(x)] + g[h(x)]
= foh(x) + goh(x)
(f+g) oh = foh + goh
(f * g) oh(x) = (f * g) oh(x)
= (f * g) [h(x)]
= f[h(x)] * g[h(x)]
= foh(x) * goh (x)
(f * g) oh = (foh) * (goh)
问题3:如果有,请检查gof和雾
(i)f(x)= | x |和g(x)= | 5x – 2 |
(ii)f(x)= 8x 3和g(x)= x 1/3
解决方案:
(i) We have,
f(x) = |x| and g (x) = | 5x – 2 |
gof(x) = g(f(x)) = g(|x|)
=> gof(x) = | 5 |x|-2 |
fog(x) = f(g(x)) = f(|5x-2|)
=> fog(x) = || 5x-2|| = | 5x -2 |
(ii) We have,
f(x) = 8x3 and g(x) = x1/3
gof(x) = g(f(x)) = g(8x3)
=> gof(x) = (8x3)1/3 = 2x
fog(x) = f(g(x)) = f(x1/3)
=> fog(x) = 8(x1/3)3 = 8x
问题4.如果f(x)= 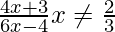 ,证明所有的fof(x)= x
,证明所有的fof(x)= x  。 f的逆是什么?
。 f的逆是什么?
解决方案:
Given that,
![]()
Now,
fof(x) = f(f(x)) = ![]()
= 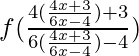
On simplifying by taking LCM = (6x-4)
fof(x) = ![]()
=> fof (x) = ![]() = x
= x
=> fof(x) = IA (x) for all ![]()
=> fof(x) = IA such that A = R – ![]() which is the domain of f
which is the domain of f
=> f-1 = f
Hence, proved.
问题5.有理有据地说明以下函数是否具有反函数。找到逆,如果存在的话。
(i)f:{1、2、3、4}-> {10}
与f = {(1,10),(2,10),(3,10),(4,10)}
(ii)g:{5,6,7,8}-> {1,2,3,4}
g = {(5,4),(6,3),(7,4),(8,2)}
(iii)h:{2,3,4,5}-> {7,9,11,13}
与h:{(2,7),(3,9),(4,11),(5,13)}
解决方案:
(i) We have f(1) = f(2) = f(3) = f(4) = 10 which means that f is many-one
and not one-one, therefore inverse of f does not exist.
(ii) Here g(5) = g(7) =4 i.e. g is many-one, so inverse of g does not exist.
(iii) Since range of h = {7, 9, 11, 13} = co-domain, therefore h is onto,
Also, each element of domain has a unique image in h, therefore h is one-one.
Now, since h is both one-one and onto,thus inverse of h exists.
h-1 = {(7, 2), (9, 3), (11, 4), (13, 5)}
问题6.证明f:[-1,1]-> R,由f(x)= 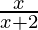 是一对一。找到函数f的反函数:{-1,1}->范围f。
是一对一。找到函数f的反函数:{-1,1}->范围f。
解决方案:
Let x, y ![]() [-1, 1]
[-1, 1]
f(x) = ![]()
f(y) = ![]()
Now,
Let f(x) = f(y)
![]()
=> x(x + 2) = y(x + 2)
=> x y + 2x = x y + 2y
=> 2x = 2y
=> x = y
=> f is one-one
Also,
X = [-1, 1] and,
Y = { ![]() } = range of f.
} = range of f.
=> f is onto
Since f is one-one and onto, therefore inverse of f exists.
Let y = f(x) => x =f-1(y)
=> y = ![]()
=> x y + 2y = x
=> 2y = x(1 – y)
=> x = ![]()
Therefore, f : Y-> X is defined by f(y) = ![]() .
.
问题7.考虑f:R-> R由f(x)= 4x + 3给出。证明f是可逆的。求f的逆。
解决方案:
It is given that,
f(x) = 4x + 3 where f : R -> R
Let,
f(x) = f(y)
=> 4x + 3 = 4y + 3
=> 4x = 4y
=> x = y
=> f is one-one function
Also,
Let y = 4x + 3 where y ![]() R
R
=> x = ![]()
![]()
Since for any ![]() . there exists
. there exists ![]() such that
such that
f(x) = ![]() = 4
= 4 ![]() +3 = y
+3 = y
=> f is onto
Since f is both one-one and onto, therefore f-1 exists
=> f-1(y) = ![]()
问题8.考虑f:R + -> [4,  )由f(x)= x 2 + 4给出。表明f是可逆的,而f的反f -1由f -1 (y)=
)由f(x)= x 2 + 4给出。表明f是可逆的,而f的反f -1由f -1 (y)=  ,其中R +是所有非负实数的集合。
,其中R +是所有非负实数的集合。
解决方案:
Let f(x) = f(y)
=> x + 4 = y + 4
=> x2 = y2
=> x = y [ x,y ![]() R+ ]
R+ ]
=> f is one-one
Let y = x2 + 4 where y ![]()
=> x2 = y – 4 ![]() 4 [ y
4 [ y ![]()
=> x = ![]()
Therefore, for any y ![]() , there exists x =
, there exists x = ![]()
![]()
=> f is onto
Since, f is both one-one and onto, f-1 exists for every ![]() ,
,
=> f-1(y) = ![]()
问题9:考虑R + -> [-5,  )由f(x)= 9x 2 + 6x -5给出。证明在f -1 (y)=时f是可逆的
)由f(x)= 9x 2 + 6x -5给出。证明在f -1 (y)=时f是可逆的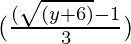
解决方案:
Let f(x) = f(y)
=> 9x2 + 6x -5 = 9y2 + 6y – 5
=> 9x2 + 6x = 9y2 + 6y
=> 9(x2 – y2) + 6 (x – y) = 0
=> (x – y) [9 (x + y) + 6] = 0
=> x – y =0
=> x = y
=> f is one-one
Now, let y = 9x2 + 6x – 5
=> 9x2 + 6x – 5 (x + y) = 0
=> x = ![]()
=> f(x) = ![]()
On simpliying, we have f (x) = y
=> f is onto
Since f is both one-one and onto. f-1 exists
f-1(y) = ![]()
问题10.让f:X-> Y是一个可逆函数。证明f具有唯一的逆。
解决方案:
We have,
f : X -> Y is an invertible function
Let g and h be two distinct inverses of f.
Then, for all y![]() Y,
Y,
fog (y) = I (y) = foh (y)
=> f g (y)) = f(h (y))
=> g(y) = h(y) [f is one-one]
=> g = h [g is one-one]
which contradicts our supposition.
Hence, f has a unique inverse.
问题11。考虑f:{1,2,3}-> {a,b,c}由f(1)= a,f(2)= b,f(3)= c给出。找到f并证明(f -1 )f -1 = f。
解决方案:
Given that,
f(1) = a, f(2) = b, f(3) = c
We have,
f = {(1, a), (2, b), (c, 3)}
which shows that f is both one-one and onto and thus f is invertible.
Therefore,
f-1 = {(a, 1), (b, 2), (c, 3)}
Also,
(f-1)-1 = {(1, a), (2,b), (3, c)}
=> (f-1)-1 = f
Hence proved.
问题12.让f:X-> Y是一个可逆函数。证明f -1的倒数是f,即(f -1 ) -1 = f。
解决方案:
Since, f is an invertible function,
=> f is both one-one and onto
Also,
Let g : Y -> X , where g is a one-one and onto function such that
gof (x) = Ix and fog (y) = Iy => g = f-1
=> f-1 o (f-1)-1 = I
=> f o [f-1 o (f-1)-1] = f o I
=> (f o f-1) o (f-1)-1 = f
=> I o (f-1)-1 = f
Hence, (f-1)-1 = f
问题13.如果f:R-> R由f(x)=(3 – x 3 ) 1/3给出,则fof(x)为:
(A)x 1/3 (B)x 3 (C)x。 (D)(3 – x 3 )
解决方案:
Answer: (C)
We have,
f(x) = (3 – x3)1/3 where f : R -> R
Now,
fof(x) = f(f(x))
=> fof(x) = f((3 – x3)1/3)
=> fof(x) = [3 – ((3 – x3)1/3 )3]1/3
=> fof(x) = [3 – (3 – x3)]1/3
=> fof(x) = (x3)1/3
=> fof(x) = x
Hence, option C is correct.
问题14.让f:R-{ 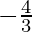 }-> R是定义为f(x)=的函数
}-> R是定义为f(x)=的函数 。 f的倒数是映射g:范围f-> R – {
。 f的倒数是映射g:范围f-> R – { 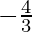 }由
}由
(A)g(y)= ![]() (B)g(y)=
(B)g(y)= ![]()
(C)g(y)= ![]() (D)g(y)=
(D)g(y)= ![]()
解决方案:
Answer: (B)
Let y = f(x)
=> y = ![]()
=> 3xy + 4y = 4x
=> x( 4 – 3y) = 4y
=> x = ![]()
f-1(y) = g (y) = ![]()