第12类NCERT解决方案-数学第I部分-第1章关系和函数-第1章的其他练习|套装1

问题1.设f： R→R定义为f(x)= 10x +7。找到函数g： R→R ，使gof = fog = 1 _R。

解决方案：

As, it is mentioned here

f : R → R be defined as f(x) = 10x + 7

To, prove the function one-one

Let’s take f(x) = f(y)

10x + 7 = 10y + 7

x = y

Hence f is one-one.

To, prove the function onto

y ∈ R, y = 10x+7

$x = \frac{y-7}{10} ∈ R$

So, it means for y ∈ R, there exists $x = \frac{y-7}{10}$

$f(x) = f(\frac{y-7}{10}) = 10(\frac{y-7}{10})+7 = y - 7 + 7 = y$

Hence f is onto.

As, f is one-one and onto. This f is invertible function.

Let’s say g : R → R be defined as $g(y) = \frac{y-7}{10}$

$g o f = g(f(x)) = g(10x+7) = \frac{(10x+7)-7}{10} = \frac{10x}{10} = x$

$f o g = f(g(x)) = f(\frac{x-7}{10}) = 10(\frac{x-7}{10})+7 = x - 7 + 7 = x$

Hence, g : R → R such that g o f = f o g = 1_R.

g : R → R is defined as $g(y) = \frac{y-7}{10}$

问题2。令f：W→W定义为f(n)= n – 1，如果n为奇数，而f(n)= n + 1，如果n为偶数。证明f是可逆的。求f的逆。在此，W是所有整数的集合。

解决方案：

The function f is defined as

$f(n)= \begin{cases} n-1, \hspace{0.2cm}n \hspace{0.2cm}is\hspace{0.2cm} odd\\ n+1,\hspace{0.2cm}n \hspace{0.2cm}is\hspace{0.2cm} even \end{cases}$

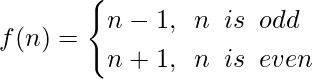
As, we know f is invertible, if and only if f is one-one and onto.

ONE-ONE

For the pair of number, we will deal with three cases:

Case 1: When both numbers p and q are odd numbers.

f(p) = p-1

f(q) = q-1

f(p) = f(q)

p-1 = q-1

p – q = 0

Case 2: When both numbers p and q are even numbers.

f(p) = p+1

f(q) = q+1

f(p) = f(q)

p+1 = q+1

p – q = 0

Case 3: When p is odd and q is even

f(p) = p-1

f(q) = q+1

f(p) = f(q)

p-1 = q+1

p – q = 2

Subtracting an odd number and even always gives a odd number, not even. Hence, the case 3 result is impossible.

So, the function f is one-one, for case 1 and case 2 only.

ONTO

Case 1: When p is odd number

f(p) = p-1

y = p-1

p = y+1

Hence, when p is odd y is even.

Case 2: When p is even number

f(p) = p+1

y = p+1

p = y-1

Hence, when p is even y is odd.

So, it means for y ∈ W, there exists p = y+1 and y-1 for odd and even value of p respectively.

Hence f is onto.

As, f is one-one and onto. This f is an invertible function.

Let’s say g : W → W be defined as 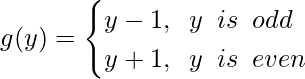$g(y)= \begin{cases} y-1, \hspace{0.2cm}y \hspace{0.2cm}is\hspace{0.2cm} odd\\ y+1,\hspace{0.2cm}y \hspace{0.2cm}is\hspace{0.2cm} even \end{cases}$

f = g

Hence, The inverse of f is f itself

问题3.如果f： R→R由f(x)= x ² – 3x + 2定义，则求f(f(x))。

解决方案：

f(x) = x²– 3x + 2

f(f(x)) = f(x²– 3x + 2)

= (x²– 3x + 2)2 – 3(x²– 3x + 2) + 2

= x⁴ + 9x² + 4 -6x³ – 12x + 4x² – 3x² + 9x – 6 + 2

f(f(x)) = x⁴ – 6x³ + 10x² – 3x

问题4：证明由f(x)定义的函数f：R→{x∈R：– 1 ，x∈R是1且在函数。

解决方案：

As, it is mentioned here

f : R → {x ∈ R : – 1 < x < 1} defined by $f(x) = \frac{x}{1+|x|}$, x ∈ R

As, we know f is invertible, if and only if f is one-one and onto.

ONE-ONE

For the pair of number, we will deal with three cases:

Case 1: When both numbers p and p are positive numbers.

The function f is defined as

Case 1: When both numbers p and q are positive numbers.

$f(p) = \frac{p}{1+|p|}$

$f(q) = \frac{q}{1+|q|}$

f(p) = f(q)

$\frac{p}{1+|p|} = \frac{q}{1+|q|}$

$\frac{p}{1+p} = \frac{q}{1+q}$

p(1+q) = q(1+p)

p = q

Case 2: When number p and q are negative numbers.

$f(p) = \frac{p}{1+|p|}$

$f(q) = \frac{q}{1+|q|}$

f(p) = f(q)

$\frac{p}{1+|p|} = \frac{q}{1+|q|}$

$\frac{p}{1-p} = \frac{q}{1-q}$

p(1-q) = q(1-p)

p = q

Case 3: When p is positive and q is negative

$f(p) = \frac{p}{1+|p|}$

$f(q) = \frac{q}{1+|q|}$

f(p) = f(q)

$\frac{p}{1+|p|} = \frac{q}{1+|q|}$

$\frac{p}{1+p} = \frac{q}{1-q}$

p(1-q) = q(1+p)

p + q = 2pq

Here, RHS will be negative and LHS will be positive. Hence, the case 3 result is impossible.

So, the function f is one-one, for case 1 and case 2.

ONTO

Case 1: When p>0.

$f(p) = \frac{p}{1+|p|}$

$y = \frac{p}{1+p}$

$p = \frac{y}{1-y} (y≠1)$

Case 2: When p <0

$f(p) = \frac{p}{1+|p|}$

$y = \frac{p}{1-p}$

$p = \frac{y}{1+y} (y≠-1)$

Hence, p is defined for all the values of y, p∈ R

Hence f is onto.

As, f is one-one and onto. This f is an invertible function.

问题5.证明f(x)= x ³给出的函数f： R→R是内射的。

解决方案：

As, it is mentioned here

f : R → R defined by f(x) = x³, x ∈ R

To prove f is injective (or one-one).

ONE-ONE

The function f is defined as

f(x) = x³

f(y) = y³

f(x) = f(y)

x³ = y³

x = y

The function f is one-one, so f is injective.

问题6.举两个函数f的示例： N→Z和g： Z→Z ，使得gof是单射的，而g不是单射的。

(提示：考虑f(x)= x和g(x)= | x |)。

解决方案：

Two functions, f : N → Z and g : Z → Z

Taking f(x) = x and g(x) = |x|

Let’s check, whether g is injective or not

g(5) = |5| = 5

g(-5) = |-5| = 5

As, we can see here that

Taking two integers, 5  and -5

g(5) = g(-5)

but, 5 ≠ -5

So, g is not an injective function.

Now, g o f: N → Z is defined as

g o f = g(f(x)) = g(x) = |x|

Now, as x,y∈ N

g(x) = |x|

g(y) = |y|

g(x) = g(y)

|x| = |y|

x = y (both x and y are positive)

Hence, g o f is an injective.

问题7.举两个函数f： N→N和g： N→N的示例，使gof出现在f上而不出现在f上。

(提示：考虑f(x)= x + 1并$g(x)= \begin{cases} x-1, \hspace{0.2cm}x>1\\ 1,\hspace{0.2cm}x=1 \end{cases}$

解决方案：

Two functions, f : N → N and g : N → N

Taking f(x) = x+1 and 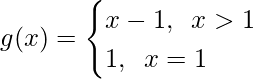$g(x)= \begin{cases} x-1, \hspace{0.2cm}x>1\\ 1,\hspace{0.2cm}x=1 \end{cases}$

 As, f(x) = x+1

y = x+1

x = y-1

But, when y=1, x = 0. Which doesn’t satiny this relation f : N → N.

Hence. f is not an onto function.

Now, g o f: N → N is defined as

g o f = g(f(x)) = g(x+1)

When x+1=1, we have

g(x+1) = 1 (1∈ N)

And, when x+1>1, we have

g(x+1) = (x+1)-1 = x

y = x, which also satisfies x,y∈ N

Hence, g o f is onto.

问题8.给定一个非空集合X，考虑P(X)，它是X的所有子集的集合。

在P(X)中定义关系R，如下所示：对于P(X)中的子集A，B，当且仅当A⊂B时，才使用ARB。R是P(X)上的等价关系吗?证明你的答案。

解决方案：

Given, A and B are the subsets of P(x), A⊂ B

To check the equivalence relation on P(X), we have to check

• Reflexive

As, we know that every set is the subset of itself.

Hence, A⊂ A and B⊂ B

ARA and BRB is reflexive for all A,B∈ P(X)

• Symmetric

As, it is given that A⊂ B. But it doesn’t make sure that B⊂ A.

To be symmetric it has to be A = B

ARB is not symmetric.

• Transitive

When A⊂ B and B⊂ C

Then of course, A⊂ C

Hence, R is transitive.

So, as R is not symmetric. 

R is not an equivalence relation on P(X).

问题9.给定一个非空集X，考虑二元运算∗：P(X)×P(X)→P(X)由A ∗ B = A∩B∀A，P(X)中的B，其中，P(X)是X的幂集。证明X是该操作的标识元素，并且X是操作∗中P(X)中唯一的可逆元素。

解决方案：

Given, P(X) × P(X) → P(X) is defined as A*B = A∩B ∀ A, B ∈ P(X)

This implies, A⊂  X and B ⊂  X

So, A∩X = A and B∩X = B ∀ A, B ∈ P(X)

⇒ A*X = A and B*X = B

Hence, X is the identity element for intersection of binary operator.

问题10.从集合{1,2,3，…，n}到其本身找出所有函数的数量。

解决方案：

Onto function from the set {1,2,3,…..,n} to itself is just same as the permutations of n.

1×2×3×4×…….×n

Which is n!.