问题1:让 ,表明(aI + bA) n = a n I + na n – 1 bA,其中I是2阶恒等式, n∈N 。
,表明(aI + bA) n = a n I + na n – 1 bA,其中I是2阶恒等式, n∈N 。
解决方案:
Using mathematical induction,
Step 1: Let’s check for n=1
(aI + bA)n = (aI + bA)1 = (aI + bA)
anI + nan – 1 bA = aI + 1a1 – 1 bA = (aI + bA)
It is true for P(1)
Step 2: Now take n=k
(aI + bA)k = akI + kak – 1 bA …………………(1)
Step 3: Let’s check whether, its true for n = k+1
(aI + bA)k+1 = (aI + bA)k (aI + bA)
= (akI + kak – 1 bA) (aI + bA)
= ak+1I×I + kak bAI + ak bAI + kak-1 b2AA
AA = 
= ak+1I×I + kak bAI + ak bAI + 0
= ak+1I + (k+1)ak+1-1 bA
= P(k+1)
Hence, P(n) is true.
问题2:如果 , 证明
, 证明
解决方案:
Using mathematical induction,
Step 1: Let’s check for n=1

It is true for P(1)
Step 2: Now take n=k

Step 3: Let’s check whether, its true for n = k+1

= P(k+1)
Hence, P(n) is true.
问题3:如果 , 证明
, 证明 ,其中n是任何正整数。
,其中n是任何正整数。
解决方案:
Using mathematical induction,
Step 1: Let’s check for n=1

It is true for P(1)
Step 2: Now take n=k

Step 3: Let’s check whether, its true for n = k+1

= P(k+1)
Hence, P(n) is true.
问题4.如果A和B是对称矩阵,则证明AB – BA是歪斜对称矩阵。
解决方案:
As, it is mentioned that A and B are symmetric matrices,
A’ = A and B’ = B
(AB – BA)’ = (AB)’ – (BA)’ (using, (A-B)’ = A’ – B’)
= B’A’ – A’B’ (using, (AB)’ = B’A’)
= BA – AB
(AB – BA)’ = – (AB – BA)
Hence, AB – BA is a skew symmetric matrix
问题5。证明矩阵B′AB是对称或倾斜对称的,因为A是对称或倾斜对称的。
解决方案:
Let’s take A as symmetric matrix
A’ = A
Then,
(B′AB)’ = {B'(AB)}’
= (AB)’ (B’)’ (using, (AB)’ = B’A’)
= B’A’ (B) (using, (AB)’ = B’A’ and (B’)’ = B)
= B’A B
As, here (B′AB)’ = B’A B. It is a symmetric matrix.
Let’s take A as skew matrix
A’ = -A
Then,
(B′AB)’ = {B'(AB)}’
= (AB)’ (B’)’ (using, (AB)’ = B’A’)
= B’A’ (B) (using, (AB)’ = B’A’ and (B’)’ = B)
= B'(-A) B
= – B’A B
As, here (B′AB)’ = -B’A B. It is a skew matrix.
Hence, we can conclude that B′AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
问题6:如果矩阵,则找到x,y,z的值 满足等式A′A = I
满足等式A′A = I
解决方案:


A’A = 



By evaluating the values, we have
2x2 = 1
x = ± ![]()
6y2 = 1
y = ± ![]()
3z2 = 1
z = ± ![]()
问题7:x的值是多少? 
解决方案:
问题8:如果 ,表明A 2 – 5A + 7I = 0。
,表明A 2 – 5A + 7I = 0。
解决方案:
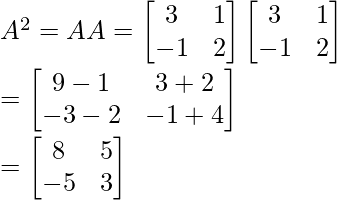


A2 – 5A + 7I = 
Hence proved!
问题9:找到x,如果
解决方案:
问题10:制造商生产三种产品x,y,z,并在两个市场上销售。
年销售额如下所示:
| Market | Products | ||
| I | 10,000 | 2,000 | 18,000 |
| II | 6,000 | 20,000 | 8,000 |
(a)如果x,y和z的单位销售价格分别为₹2.50,₹1.50和₹1.00,请借助矩阵代数找到每个市场的总收入。
解决方案:
Total revenue in market I and II can be arranged from given data as follows:
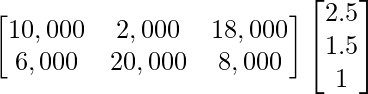
After multiplication, we get
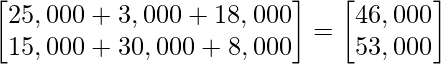
Hence, the total revenue in Market I and market II are ₹ 46,000 and ₹ 53,000 respectively.
(b)如果上述三种商品的单位成本分别为2.00卢比,1.00卢比和50帕斯。找到毛利润。
解决方案:
Total cost prices of all the products in market I and market II can be arranged from given data as follows:

After multiplication, we get

As, Profit earned = Total revenue – Cost price
Profit earned 
Profit earned = 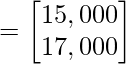
Hence, profit earned in Market I and market II are ₹ 15,000 and ₹ 17,000 respectively. Which is equal to ₹ 32,000
问题11。找到矩阵X,这样
解决方案:

Here, the RHS is a 2×3 matrix and LHS is 2×3. So, X will be 2×2 matrix.
Let’s take X as,

Now solving the matrix, we have

Equating each of them, we get
p+4q = -7 ………..(1)
2p+5q = -8 ………….(2)
3p + 6q = -9
r + 4s = 2 …………(3)
2r + 5s = 4 ……………(5)
3r + 6s = 6
Solving (1) and (2), we get
p = 1 and q = -2
Solving (3) and (4), we get
r = 2 and s = 0
Hence, matrix X is

问题12:如果A和B是相同阶的平方矩阵,从而AB = BA,则通过归纳证明AB n = B n A.此外,对于所有n∈N证明(AB) n = A n B n 。
解决方案:
Using mathematical induction,
Step 1: Let’s check for n=1
ABn = AB1 = AB
BnA = B1A = BA
It is true for P(1)
Step 2: Now take n=k
ABk = BkA
Step 3: Let’s check whether, its true for n = k+1
AB(k+1) = ABkB
= BkAB
= Bk+1 A
= P(k+1)
Hence, P(n) is true.
Now, for (AB)n = AnBn
Using mathematical induction,
Step 1: Let’s check for n=1
(AB)1 = AB
B1A1 = BA
It is true for P(1)
Step 2: Now take n=k
(AB)k = AkBk
Step 3: Let’s check whether, its true for n = k+1
(AB)(k+1) = (AB)k(AB)
= AkBk AB
= Ak+1 Bk+1
= (AB)k+1
= P(k+1)
Hence, P(n) is true.
在以下问题中选择正确的答案:
问题13:如果 使得A²= I,那么
使得A²= I,那么
(A)1 +α²+βγ= 0
(B)1 –α²+βγ= 0
(C)1 –α²–βγ= 0
(D)1 +α²–βγ= 0
解决方案:

As, A2 = I

α² + βγ = 1
1 – α² – βγ = 0
Hence, Option (C) is correct.
问题14:如果矩阵A既是对称的又是倾斜对称的,则
(A)A是对角矩阵
(B)A是零矩阵
(C)A是一个方矩阵
(D)这些都不是
解决方案:
If the matrix A is both symmetric and skew symmetric, then
A = A’
and A = -A
Only zero matrix satisfies both the conditions.
Hence, Option (B) is correct.
问题15。如果A是方阵使得A 2 = A,则(I + A)³– 7 A等于
(A)A
(B)我– A
(C)我
(D)3A
解决方案:
(I + A)³ – 7 A = I3 + A3 + 3A^2 + 3AI^2 – 7A
= I3 + A3 + 3A2 + 3A – 7A
= I + A3 + 3A2 – 4A
As, A2 = A
A3 = A2A = AA = A
So, I + A3 + 3A2 – 4A = I + A + 3A – 4A = I
Hence, Option (C) is correct.




