问题1:多面体可以面对吗
(i)3个三角形? (ii)4个三角形? (iii)一个正方形和四个三角形?
解决方案:
(i) 3 triangles: No, because polyhedron must have minimum 4 faces i.e all edges should meet at vertices.
(ii) 4 triangles: Yes, as all the edges are meeting at the vertices and has four triangular faces.
(iii) a square and four triangles: Yes, because all the eight edges meet at the vertices having a square face and four triangular faces.
问题2:是否可以使用具有给定数量的面的多面体? (提示:想想一个金字塔)。
解决方案:
Yes, It is possible to have a polyhedron with any given faces only if the number of faces are greater than or equal to four.
问题3:以下哪个棱镜?
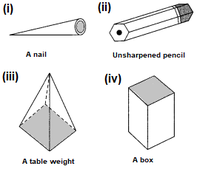
解决方案:
Prisms among the given images are
(ii) Unsharpened pencil
(iv) A box.
问题4: (i)棱镜和圆柱体如何相似? (ii)金字塔和圆锥体如何相似?
解决方案:
(i) If the number of sides in a prism are increased to certain extent, then the prism will take the shape of cylinder i.e. a prism with a circular base.
(ii) If the number of sides of the pyramid is increased to same extent, then the pyramid becomes a cone i.e. a pyramid with a circular base.
问题5:方棱镜和立方体相同吗?解释。
解决方案:
Yes, a square prism can be same as a cube, but if the height of the prism is greater than It may be cuboid.
问题6:验证这些固体的欧拉公式。
(一世)
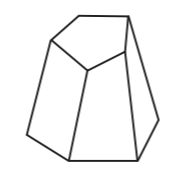
(ii)

解决方案:
(i) No. of Faces (F) = 7
No. of Vertices (V) = 10
No. of Edges (E) = 15
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ 7 + 10 – 15 = 2
⇒ 2 = 2
Therefore, Euler’s formula is verified.
(ii) No. of Faces (F) = 9
No. of Vertices (V) = 9
No. of Edges (E) = 16
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ 9 + 9 – 16 = 2
⇒ 2 = 2
Therefore, Euler’s formula is verified.
问题7:使用欧拉公式找出未知数。
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
解决方案:
(i)
No. of Faces (F) = F
No. of Vertices (V) = 6
No. of Edges (E) = 12
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ F + 6 – 12 = 2
⇒ F = 2 + 6
⇒ F = 8
Therefore, No. of Faces (F) = 8
(ii)
No. of Faces (F) = 5
No. of Vertices (V) = V
No. of Edges (E) = 9
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ 5 + V – 9 = 2
⇒ E = 2 + 4
⇒ E = 6
Therefore, No. of Vertices (V) = 6
(iii)
No. of Faces (F) = 20
No. of Vertices (V) = 12
No. of Edges (E) = E
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ 20 + 12 – E = 2
⇒ E = 32 – 2
⇒ E = 30
Therefore, No. of Edges (E) = 30
问题8:多面体可以有10个面,20个边和15个顶点吗?
解决方案:
Since every polyhedron satisfies Euler’s formula, therefore checking if polyhedron can have 10 faces, 20 edges and 15 vertices.
No. of Faces (F) = 10
No. of Vertices (V) = 15
No. of Edges (E) = 20
By Using Euler’s formula: F + V – E = 2 and Substituting the values, we get
⇒ 10 + 15 – 20 = 2
⇒ -5 = 2
As Euler’s formula is not satisfied, therefore polyhedron cannot have 10 faces, 20 edges and 15 vertices.