11类NCERT解决方案-第10章直线–练习10.1

问题1.在笛卡尔平面上绘制一个四边形，其顶点为(– 4，5)，(0，7)，(5，– 5)和(– 4，–2)。另外，找到其区域。

解决方案：

Let’s consider the quadrilateral ABCD with vertices A (-4,5), B (0,7), C (5.-5) and D (-4,-2).

After plotting the points on the Cartesian plane we get the required quadrilateral :

Construction : Join diagonal AC

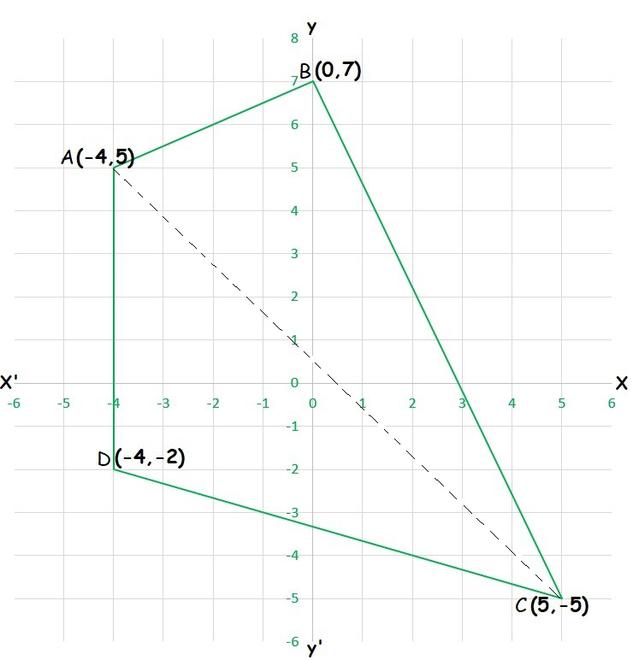
Area (ABCD) = area (∆ABC) + area (∆ADC)

Then, area of triangle with vertices (x₁,y₁), (x₂, y₂) and (x₃,y₃) is

= |½ [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]|

So,

Area (∆ABC)= |½ [-4 (7 + 5) + 0 (-5 – 5) + 5 (5 – 7)] |

= |½ [-4 (12) + 5 (-2)] |

= |½ [-48 -10)] |

= | ½ (58) |

= 29 sq. unit

Area (∆ACD) = |½ [-4 (-5 + 2) + 5 (-2 – 5) + (-4) (5 – (-5))]|

= |½ [-4 (-3) + 5 (-7) – 4 (10)]|

= |½ [-12 + -35 – 40]|

= |½ (-63)|

= 63/2 sq. unit

Area (ABCD) = 29 + 63/2

= 121/2 sq. unit

问题2。等边三角形的边为2a的底边沿y轴放置，以使底边的中点位于原点。查找三角形的顶点。

解决方案：

Let’s consider ∆ABC, which is an equilateral triangle with side 2a.

Where, AB = BC = AC = 2a

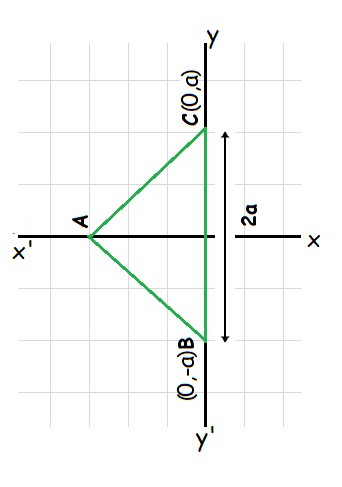
As in the figure, we assume BC as base, where origin becomes mid-point of BC. So, we can conclude that

The co-ordinates of point C are (0, a) and that of B are (0,-a).

And as origin is the mid-point, so the line joining vertex and origin lies on x-axis. (x-axix ⊥ y-axis)

(AC)² = OA² + OC²        (Pythagoras theorem)

(2a)²= a² + OA²

4a² – a² = OA²

OA² = 3a²

OA =√3a

Co-ordinates of point A = ± (√3a, 0)

∴ The vertices of the given equilateral triangle are (0, a), (0, -a), (√3a, 0) Or (0, a), (0, -a) and (-√3a, 0)

问题3.在以下情况下找到P(x ₁ ，y ₁ )与Q(x ₂ ，y ₂ )之间的距离：

(i)PQ平行于y轴，

(ii)PQ平行于x轴。

解决方案：

(i) When PQ is parallel to the y-axis, then the x-coordinates will be same.

so, x₁=x₂

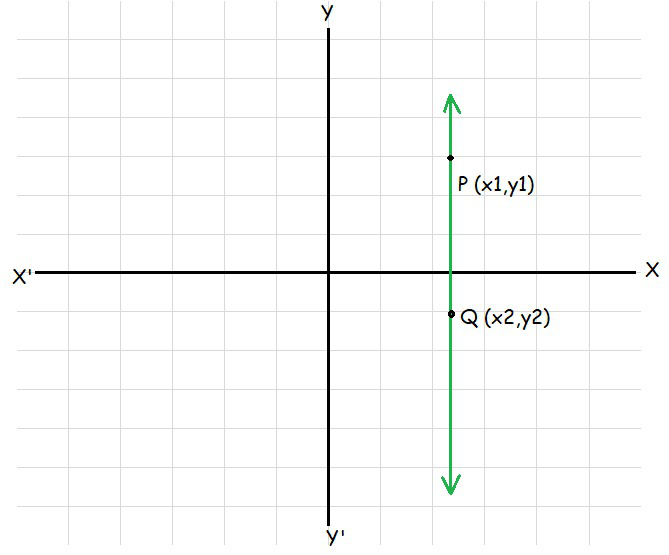
Distance between points PQ = √((x₁-x₂)² + (y₁-y₂)²)

= √(y₁-y₂)²                         (As x₁=x₂)

= |y₁-y₂|

(ii)

When PQ is parallel to the x-axis, then, the y-coordinates will be same.

so, y₁=y₂

Distance between points PQ = √((x₁-x₂)2 + (y₁-y₂)²)

= √(x₁-x₂)²                         (As y₁=y₂)

= |x₁-x₂|

问题4.在x轴上找到一个与点(7，6)和(3，4)等距的点。

解决方案：

As it is mentioned that, these points A and B are equidistant from a point P on x-axis.

Let’s take P as (a, 0).

Distance AP = Distance BP

Distance between two points (x₁,y₁) and (x₂,y₂)= √((x₁-x₂)² + (y₁-y₂)²)

so, 

√((3-a)² + (4-0)²) = √((7-a)² + (6-0)²)

√((3-a)² + 16) = √((7-a)² + 36)

√(9-6a+a²+16) = √(49-14a+a²+36)

Squaring both sides, we get

a² – 6a + 25 = a² – 14a + 85

-8a = -60

a = 15/2

Hence, the point on the x-axis, which is equidistant from the points (7, 6) and (3, 4) is (15/2,0)

问题5.找到一条直线的斜率，该斜率穿过原点，并将线段的中点连接到点P(0，– 4)和点B(8，0)。

解决方案：

Let the co-ordinates of mid-point of the line segment joining the points P (0, – 4) and B (8, 0) be (x,y), so 

x = (0+8)/2 = 4

y = (-4+0)/2 = -2

Mid point is (4,-2)

As The slope ‘m’ of the line which is passing through the point (x₁,y₁) and (x₂,y₂) will be given as

m = (y₂ – y₁)/(x₂ – x₁) where, (x₂ ≠ x₁)

So now, The slope ‘m’ of the line which is passing through the point (4,-2) and origin (0,0) will be

m = (4-0)/(-2-0) = 4/-2 = -1/2

Hence, the required slope is -1/2.

问题6.不使用毕达哥拉斯定理，请证明点(4，4)，(3，5)和(–1，–1)是直角三角形的顶点。

解决方案：

As the vertices of the given triangle are (4, 4), (3, 5) and (–1, –1).

As The slope ‘m’ of the line which is passing through the point (x₁,y₁) and (x₂,y₂) will be given as

m = (y₂ – y₁)/(x₂ – x₁) where, (x₂ ≠ x₁)

Let m₁ be the slope of the line AB, then 

m₁ = (4 –(-1))/(4 –(-1)) = 1 ……………….(1)

Let m₂ be the slope of the line BC, then

m₂ = (3-4)/(5-4) = -1  …………………….(2)

Let m₃ be the slope of the line AC, then

m₃ = (5-(-1))/(3-(-1)) = 6/4 = 3/2  ………………..(3)

From (1) and (2), we can conclude

m₁.m₂ = -1.1 = -1

Hence, the lines AB and BC are perpendicular to each other.

Hence, given triangle is right-angled at B (4, 4)

问题7.找到直线的斜率，该斜率与y轴的正方向逆时针方向成30°角。

解决方案：

We know that if a line makes an angle of 30° with the positive direction of y-axis measured anti-clock-wise , then the angle made by the line with the positive direction of x- axis measure anti-clock-wise is 

90° + 30° = 120°

∴ The slope of the given line is 

tan(120°) = tan (180° – 60°)

= – tan 60°

= –√3

问题8.找到点(x，– 1)，(2,1)和(4，5)共线的x的值。

解决方案：

If the points (x, – 1), (2, 1) and (4, 5) are collinear, then 

Slope of AB = Slope of BC

Slope of AB = (1-(-1))/(2-x)

= 2/(2-x) ……………….(1)

Slope of BC = (5-1)/(4-2)

 = 4/2

= 2  ………………..(2)

from (1) and (2)

2 = 2(2-x)

2 = 4 – 2x

2x = 4 – 2

2x = 2

x = 2/2

= 1

Hence, the required value of x is 1.

问题9.在不使用距离公式的情况下，请显示点(– 2，– 1)，(4，0)，(3，3)和(–3，2)是平行四边形的顶点。

解决方案：

Let the given point be A (4, 0) , B ( 3, 3) C ( -3, 2) and D (-2, -1) of quadrilateral.

So now, The slope of AD = (0-(-1))/(4-(-2)) = 1/6

The slope of BC = (3-2)/(3-(-3)) = 1/6

Hence, slope of AD = Slope of BC

Hence, AD ∥ BC ……………………..(1)

Now,

The slope of AB = (3-0)/(3-4) = 3/-1 = -3

The slope of CD = (2-(-1))/(-3-(-2)) = 3/-1 = -3

Hence, slope of AB = Slope of CD

Hence, AB ∥ CD ……………………(2)

Hence, from (1) and (2), we can conclude that

The pair of opposite sides are quadrilateral are parallel, so we can say that ABCD is a parallelogram.

Hence the given vertices, A (4, 0), B (3, 3) C (-3, 2) and D (-2, -1) are vertices of a parallelogram.

问题10.找到x轴与连接点(3，–1)和(4，–2)的线之间的角度。

解决方案：

As The slope ‘m’ of the line which is passing through the point (x1,y1) and (x2,y2) will be given as

m = (y2 – y1)/(x2 – x1) where, (x2 ≠ x1)

So now, The slope ‘m’ of the line which is passing through the point (3,–1) and (4,–2) will be

m = (-2 –(-1))/(4-3)

= (-2+1)/(4-3)

= -1/1

= -1

as, m = tan θ

tan θ = -1

θ = (90° + 45°) = 135°

Hence, The angle between the x-axis and the line joining the points (3, –1) and (4, –2) is 135°.

问题11.一条线的斜率是另一条线的斜率的两倍。如果它们之间的角度的切线为1/3，则找到直线的斜率。

解决方案：

Let us consider ‘m1’ and ‘m’ be the slope of the two given lines such that m1 = 2m and,

tan θ = 1/3

We know that if θ is the angle between the lines l1 and l2 with slope m1 and m2, then

tan θ = |(m2-m1) /(1+m1m2)|

so here,

1/3 = |(2m-m) /(1+2m²)|

1/3 = |m/(1+2m²)|

1/3 = ± (m/(1+2m²)) 

So taking, CASE 1

1/3 = + (m/(1+2m²))

2m² – 3m + 1 = 0

2m² – 2m – m + 1 = 0

2m (m – 1) – 1(m – 1) = 0

m = 1 or 1/2 ……………..(1)

And now, solving CASE 2

1/3 = – (m/(1+2m²))

1+2m² = -3m

2m² +1 +3m = 0

2m (m+1) + 1(m+1) = 0

(2m+1) (m+1)= 0

m = -1 or -1/2 ………………………(2)

So from (1) and (2) we can conclude that,

The pairs of slopes can be (1 and 2), (-1 and -2), (1 and 1/2) and (-1 and -1/2).

问题12.一条线穿过(x1，y1)和(h，k)。如果直线的斜率是m，则表明

k – y1 = m(h – x1)

解决方案：

As it is given that, the slope of the line is ‘m’

The slope of the line passing through (x1, y1) and (h, k) is (k – y1)/(h – x1)

So,

m = (k – y1)/(h – x1)

(k – y1) = m (h – x1)

Hence, proved.

问题13：如果三个点(h，0)，(a，b)和(0，k)在一条线上，则表明a / h + b / k = 1。

解决方案：

If the given points A (h, 0), B (a, b) and C (0, k) lie on a line, then,

Slope of AB = slope of BC

(b – 0)/(a – h) = (k – b)/(0 – a)

By simplifying, we get

-ab = (k-b) (a-h)

-ab = ka- kh –ab +bh

ka +bh = kh

Divide both the sides by kh we get,

ka/kh + bh/kh = kh/kh

a/h + b/k = 1

Hence, proved.

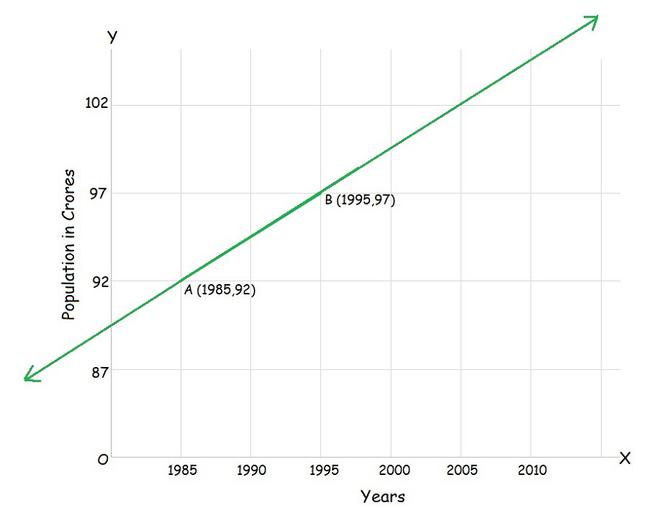
问题14.考虑以下人口和年图(图10.10)，找到AB线的斜率并使用它，求出2010年的人口是多少?

解决方案：

As The slope ‘m’ of the line which is passing through the point (x1,y1) and (x2,y2) will be given as

m = (y2 – y1)/(x2 – x1) where, (x2 ≠ x1)

So, the slope ‘m’ of the line which is passing through the point (1985,92) and (1995,97) will be given as

m = (97 – 92)/(1995 – 1985) = 5/10 = 1/2

Let ‘y’ be the population in the year 2010. Then, according to the given graph, AB must pass through point C (2010, y).

slope of AB = slope of BC

1/2 = (y-97)/(2010-1995)

15/2 = y – 97

y = 7.5 + 97 = 104.5

Hence, the slope of the line AB is 1/2, and

In the year 2010 the population will be 104.5 crores.