第10类NCERT解决方案-第10章圈子-练习10.2

Theorem 10.1(NCERT) : The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Theorem 10.2 (NCERT) : The lengths of tangents drawn from an external point to a circle are equal. 

在Q.1到Q.3中，选择正确的选项，然后给出理由。

问题1.从点Q开始，圆的切线长度为24厘米，而距中心的距离为25厘米。圆的半径是

(A)7厘米

(B)12厘米

(C)15厘米

(D)24.5厘米

解决方案：

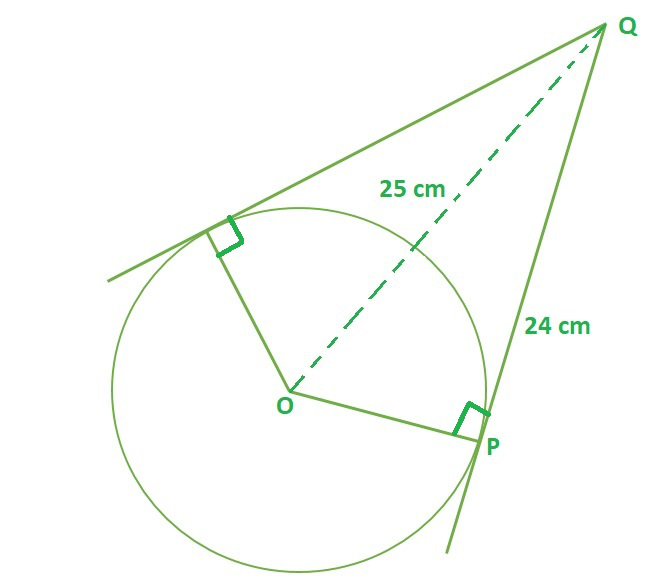
According to theorem 10.1, OP⊥ PQ then ∆OPQ is a right-angled triangle

OQ² = PQ² + OP²  (Pythagoras Theorem)

25² = 24² + OP² 

OP² = 25² – 24² 

OP² = (25+24) (25-24)                               (using identity a² – b² = (a+b)(a-b))

OP = √49

OP = 7 cm

Hence, option A is correct.

问题2。在图10.11中，如果TP和TQ是中心为O的圆的两个切线，则∠POQ = 110°，则∠PTQ等于

(A)60°

(B)70°

(C)80°

(D)90°

解决方案：

In the quadrilateral OPTQ,

∠P = 90°, ∠Q = 90°  (Theorem 10.1)

∠O = 110° 

The sum of the angles of a quadrilateral is 360° (Angle sum property of quadrilateral), Hence

∠P + ∠Q + ∠T + ∠O = 360°

90° + 90° + ∠T + 110° = 360°

∠T = 180 – 110° = 70°

Hence, option B is correct.

问题3.如果从点P到以O为中心的圆的切线PA和PB彼此倾斜80°，则∠POA等于

(A)50°

(B)60°

(C)70°

(D)80°

解决方案：

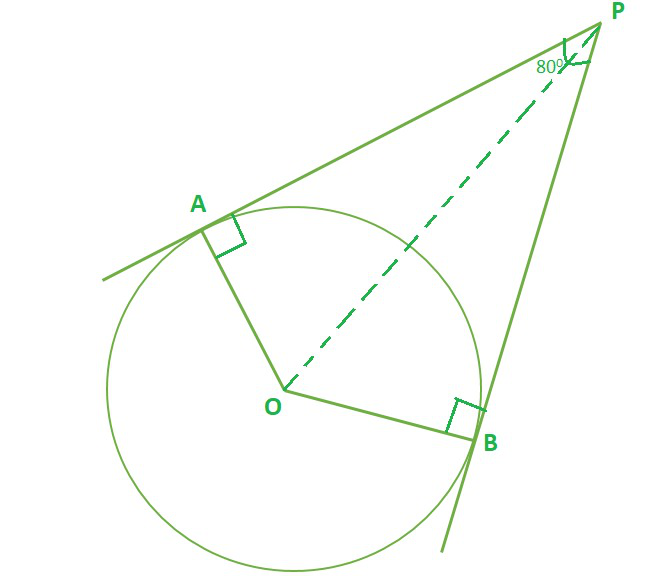
In the quadrilateral OAPB,

∠A = 90°, ∠B = 90°  (Theorem 10.1)

∠P = 80°

The sum of the angles of a quadrilateral is 360° (Angle sum property of quadrilateral), Hence

∠A + ∠B + ∠P + ∠O = 360°

90° + 90° + 80° + ∠O = 360°

∠O = 180° – 80° = 100° …………………..(1)

Considering, ∆OAP and ∆OBP

OA = OB …………..(radius of circle)

AP = BP ……………(Theorem 10.2)

∠OAP = ∠OBP …….(Theorem 10.1)

∴ ∆OAP ≅ ∆OBP           [By SAS congruency]

So, ∠AOP = ∠BOP [By C.P.C.T.]…………..(2)

From (1) and (2), we conclude that,

∠AOP + ∠BOP = 100°

∠AOP = 50°

Hence, option A is correct.

问题4.证明在圆直径的两端绘制的切线是平行的。

解决方案：

P and Q are point of contacts of Tangent lines l and m respectively.

O is the centre of circle.

OP⊥ l , OQ⊥ m and PQ is diameter (theorem 10.1)

∠PQm + ∠QPl = 90° + 90° = 180°

As, sum of adjacent angles is supplementary (180°), hence opposite sides are parallel.

问题5.证明圆的切线接触点处的垂线穿过中心。

解决方案：

P is the point of contact of tangent line l.

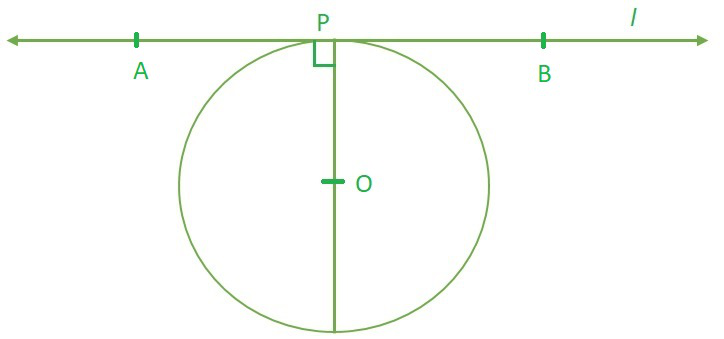
Let, OP⊥ l at Point of contact P and it passes through point O.

As, The tangent at any point of a circle is perpendicular to the radius through the point of contact. (theorem 10.1)

According to the theorem 10.1 line OP has to pass through centre of circle for sure.

问题6.距圆心5 cm处的点A的切线长度为4 cm。找到圆的半径。

解决方案：

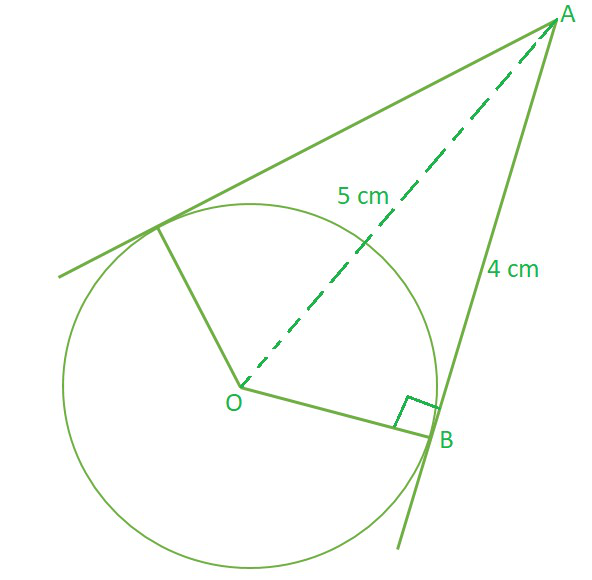
According to theorem 10.1, OB⊥ AB then ∆OAB is a right-angled triangle

OA² = AB² + OB²  (Pythagoras Theorem)

5² = 4² + OB²

OB² = 5² – 4²

OB² = (5+4) (5-4)                               (using identity a² – b² = (a+b)(a-b))

OB = √9

OB = 3 cm

Hence, Radius of circle = 3 cm

问题7.两个同心圆的半径分别为5厘米和3厘米。找到与小圆圈接触的大圆圈的和弦长度。

解决方案：

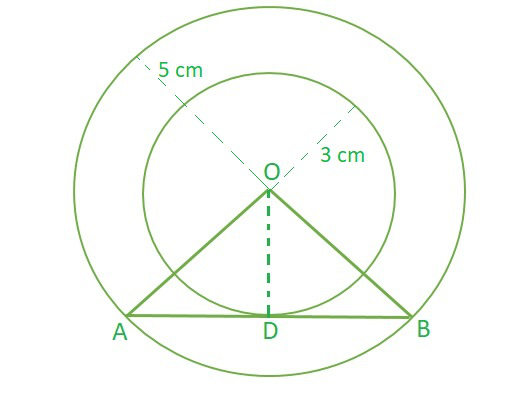
Considering, ∆OAD and ∆OBD

OA = OB …………..(radius of large circle)

OD = OD ……………(common side)

∠ADO = ∠BDO …….(each 90°)…….(Theorem 10.1)

∴ ∆OAD ≅ ∆OBD           [By SAS congruency]

So, AD = BD [By C.P.C.T.]…………….(1)

Taking ∆OAD, which 90° at ∠D

OA = OB = 5 cm (radius of large circle)

OD = 3 cm  (radius of smaller circle)

OA² = AD² + OD²  (Pythagoras Theorem)

5² = AD² + 3²

AD² = 5² – 3² 

AD² = (5+3) (5-3)

AD = √16

AD = 4 cm

AB = 2 × AD (from 1)

AB = 2 × 4

AB = 8 cm

Hence, length of the chord of the larger circle which touches the smaller circle = 8 cm

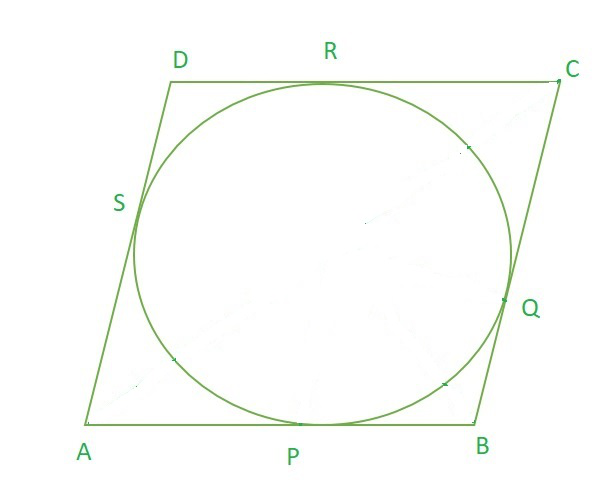
问题8：画出一个四边形的ABCD来外接一个圆(见图10.12)。证明AB + CD = AD + BC。

解决方案：

Let the P, Q, R and S be point of contacts for tangent AB, BC, CD and DA respectively .

AP = AS  (theorem 10.2)……..(1)

BP = BQ  (theorem 10.2)……..(2)

CR = CQ  (theorem 10.2)……..(3)

DR = DS  (theorem 10.2)……..(4)

By, adding (1), (2), (3) and (4) RHS = LHS, we get

AP + BP + CR + DR = AS + BQ + CQ + DS

(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)  (by Rearranging)

AB + CD = AD + BC 

Hence, proved !!

问题9。在图10.13中，XY和X’Y’是圆的两个平行切线，圆的中心为O，另一个切线AB的接触点C的交点A在XY上，X’Y’在B上。证明′AOB = 90°。

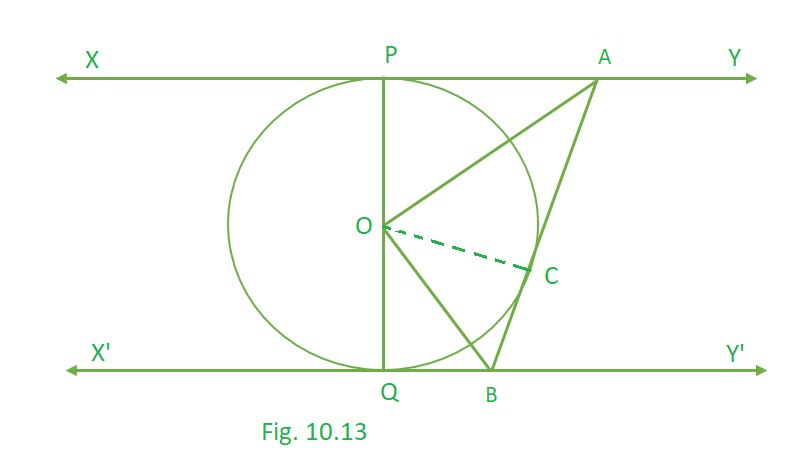
解决方案：

As we can observe here,

AP and AC are tangent at same external point A.

and, QB and BC are tangent at same external point B.

Taking, ∆OAP and ∆OAC in consideration

OP = OC …………..(radius of circle)

OA = OA ……………(common side)

∠OPA = ∠OCA …….(each 90°)…….(Theorem 10.1)

∴ ∆OAP ≅ ∆OAC           [By SAS congruency]

So, ∠POA = ∠COA [By C.P.C.T.]

we can conclude that, ∠COP = 2 ∠COA………………..(1)

Similarly, ∠COQ = 2 ∠COB ………….(2)

Adding (1) and (2), RHS = LHS we get,

2 ∠COA + 2 ∠COB = ∠COQ + ∠COP

2 (∠COA + ∠COB) = 180°  (Angle made by a straight line = 180°)

2 (∠AOB) = 180°

∠AOB = 90°.

Hence, proved !!

问题10.证明从外部点到圆的两个切线之间的角度是与连接中心的接触点的线段对向的角度的补充。

解决方案：

In the quadrilateral OPTQ,

∠P = 90°, ∠Q = 90°  (Theorem 10.1)

The sum of the angles of a quadrilateral is 360° (Angle sum property of quadrilateral), Hence

∠P + ∠Q + ∠T + ∠O = 360°

90° + 90° + ∠T + ∠O = 360°

∠T + ∠O = 180° 

Hence, Proved, the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the Centre.

问题11.证明外接圆的平行四边形是菱形。

解决方案：

ABCD is a parallelogram and let P, Q, R and S be the point of contact of circle and parallelogram.

AP = AS  (theorem 10.2)……..(1)

BP = BQ  (theorem 10.2)……..(2)

CR = CQ  (theorem 10.2)……..(3)

DR = DS  (theorem 10.2)……..(4)

By, adding (1), (2), (3) and (4) RHS = LHS, we get

AP + BP + CR + DR = AS + BQ + CQ + DS

(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)  (by Rearranging)

AB + CD = AD + BC

As ABCD is a parallelogram, AB = CD and AD = BC (Opposite sides of parallelogram are equal)

Hence, 2 AB = 2 BC

AB = BC

If adjacent side of parallelogram are equal, then it is a rhombus.

Hence, ABCD is a rhombus !!

问题12.绘制一个三角形ABC来外接一个半径为4 cm的圆，以使BC被接触点D分开的部分BD和DC的长度分别为8 cm和6 cm(见图10.14)。找到侧面AB和AC。

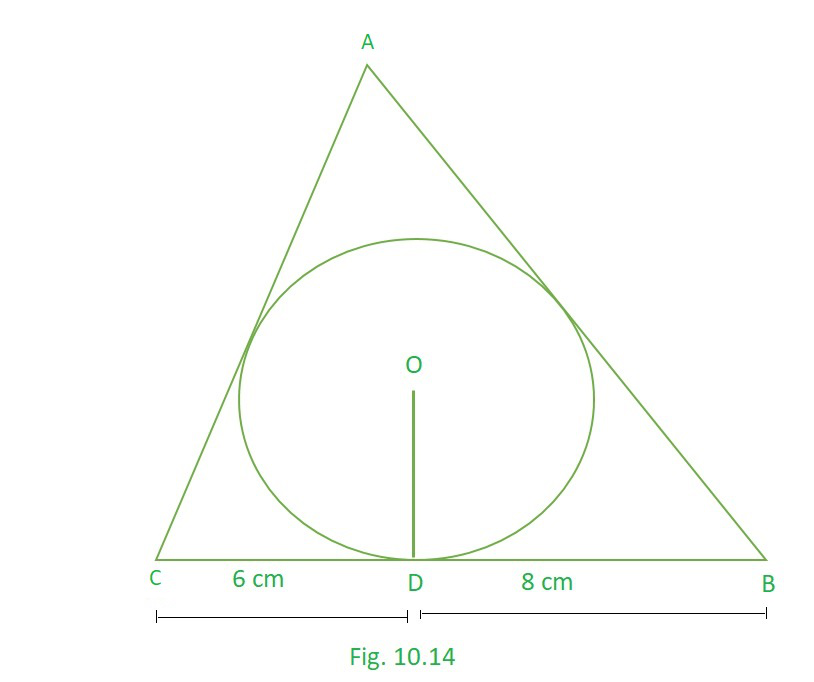
解决方案：

ABC is a Triangle and let M, D and N be the point of contact of circle and Triangle.

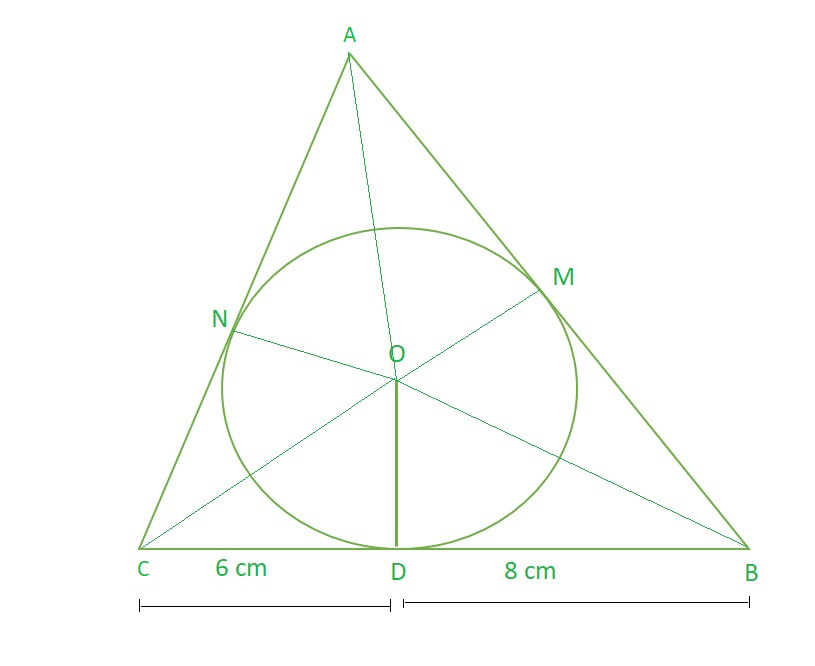
BD = BM =  8 cm (theorem 10.2)……..(1)

CN = CD  = 6 cm (theorem 10.2)……..(2)

AN = AM  = p cm (theorem 10.2)……..(3)

AB = p+8 cm

BC = 6+8 = 14 cm

AC = p+6 cm

As we can observe here that,

Area of ∆ABC = Area of ∆AOC + Area of ∆COB + Area of ∆BOA

So, Area of ∆ABC = ar(∆ABC)

√(s (s-AB) (s-AC) (s-BC))     …………(Heron’s formula)  where s = (sum of sides) / 2

s = (AB+BC+AC)/2

s = (p+8+14+p+6)/2

s = (2p+28)/2

s = p+14

ar(∆ABC) = √((p+14) (p+14-(p+8)) (p+14-(p+6)) (p+14-14))

 = √((p+14) (6) (8) (p))

= √48p (p+14) cm²……………………………………………(1)

Area of ∆AOC + Area of ∆COB + Area of ∆BOA = (½ × ON × AC) + (½ × OD × BC) + (½ × OM × AB)

= (½ × 4 × (p+6)) + (½ × 4 × 14) + (½ × 4 × (p+8))

= ½ × 4 (p+6+14+p+8)

= ½ × 4 × (2p+28)

= 4 × (p+14) cm²  ………………………………………………(2)

(1) = (2)

√48p (p+14) =  4 × (p+14)

Squaring both sides, we get

 48 × p × (p+14) = (4 × (p+14))²

48 × p (p+14) = 16 × (p+14)²             (cancelling (p+14) from both sides)

48 × p = 16 (p+14)

48p = 16p+ 224

32 × p = 224

p = 7 cm 

Hence, AB = p+8 = 7+8 = 15 cm

AC = p+6 = 7+6 = 13 cm

问题13：证明外接圆的四边形的相对侧在圆的中心对向补充角。

解决方案：

In the quadrilateral OPBQ,

∠OPB = 90° , ∠OQB = 90°  (Theorem 10.1)

Considering, ∆OPB and ∆OQB

OP = OQ …………..(radius of circle)

OB = OB ……………(Common)

∠OPB = ∠OQB …….(each 90°)……..(Theorem 10.1)

∴ ∆OPB ≅ ∆OQB           [By SAS congruency]

So, ∠POB = ∠QOB [By C.P.C.T.]

Hence, ∠1 = ∠2  ……………..(1)

Similarly, ∠3 = ∠4  ……………..(2)

∠5 = ∠6  ……………..(3)

∠7 = ∠8  ……………..(4)

By making complete revolution,

∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360° (A complete revolution makes 360°)

∠1 + ∠1 + ∠4 + ∠4 + ∠5 + ∠5 + ∠8 + ∠8 = 360°

2 (∠1 + ∠4 + ∠5 + ∠8) = 360°

2 ((∠1 + ∠8) + (∠4 + ∠5) ) = 360°

∠AOB + ∠COD = 360° / 2 = 180°

Hence, proved, that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the Centre of the circle.