9类RD Sharma解决方案–第12章苍鹭的公式-练习12.2

问题1.找到四边形ABCD的面积，其中AB = 3 cm，BC = 4 cm，CD = 4 cm，DA = 5 cm，AC = 5 cm。

解决方案：

In triangle ABC of Quadrilateral ABCD

AC² = BC² + AB²

25 = 9 + 16

Hence, triangle ABC is a right angle triangle right-angled at point R

As we know that, Area of triangle ABC = 12 × AB × BC

= 1/2 × 3 × 4 = 6 cm²

From triangle CAD,

Perimeter = 2s = AC + CD + DA

2s = 5 cm+ 4 cm+ 5 cm

2s = 14 cm

s = 7 cm

By using Heron’s Formula,

Area of triangle = √s x (s – a) x (s – b) x (s – c)

= √7 x (7 – 5) x (7 – 4) x (7 – 5) = 9.16 cm²

Area of ABCD = Area of ABC + Area of CAD

= (6 + 9.16) cm² = 15.16 cm²

问题2.四边形场的边分别是26 m，27 m，7 m，24 m。最后两个侧面包含的角度为直角。查找其区域。

解决方案：

Given that,

AB = 26 m, BC = 27 m, CD = 7 m, DA = 24 m

Diagonal AC is joined.

Now, in triangle ADC

By applying Pythagoras theorem,

AC² = AD² + CD²

AC² = 14²  + 7²

AC = 25 m

Now Area of triangle ABC,

Perimeter = 2s = AB + BC + CA

2s = 26 m + 27 m + 25 m

s = 39 m

By using Heron’s Formula,

Area of triangle ABC = √s x (s – a) x (s – b) x (s – c)

= √ 39 x (39 – 26) x (39 – 27) x (39 – 25) = 291.84 m²

Thus, Area of a triangle is 291.84 m²

Now for Area of triangle ADC,

Perimeter = 2S = AD + CD + AC

= 25 m + 24 m + 7 m

S = 28 m

By using Heron’s Formula,

Area of triangle ADC = √s x (s – a) x (s – b) x (s – c)

= √ 28 x (28 – 24) x (28 – 7) x (28 – 25) = 84 m²

Thus, Area of a triangle is 84m²

Therefore, Area of rectangular field ABCD

= Area of triangle ABC + Area of triangle ADC

= 291.84 + 84 = 375.8 m²

问题3.四边形的边，分别取为5 m，12 m，14 m，15 m，并且前两个边所成的角度为直角。查找其区域。

解决方案：

Given that,

AB = 5 m, BC = 12 m, CD =14 m and DA = 15 m

Join AC

Now area of triangle ABC = ½ × AB × BC

= 1/2× 5 × 12 = 30 m²

In triangle ABC, 

By applying Pythagoras theorem

AC² = AB² + BC²

AC = √52 + 122 = 13 m

Now in triangle ADC,

Perimeter = 2s = AD + DC + AC

2s = 15 m + 14 m + 13 m

s = 21 m

By using Heron’s Formula,

Area of triangle = √s x (s – a) x (s – b) x (s – c)

= √ 21 x (21 – 15) x (21 – 14) x (21 – 13) = 84 m²

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC

= (30 + 84) m² = 114 m²

问题4.一个四边形ABCD形状的公园，其角度C = 90°，AB = 9 m，BC = 12 m，CD = 5 m，AD = 8 m。它占用多少面积?

解决方案：

Given that,

Sides of a quadrilateral are AB = 9 m, BC = 12 m, CD = 5 m, DA = 8 m.

In triangle BCD, apply Pythagoras theorem

BD² = BC² + CD²

BD² = 12² + 5²

BD = 13 m.

Area of triangle BCD = 1/2 × BC × CD

= 1/2 × 12 × 5 = 30 m²

Now, in triangle ABD

Perimeter = 2s = 9 m + 8m + 13m

s = 15 m

By using Heron’s Formula,

Area of triangle = √s x (s – a) x (s – b) x (s – c)

= √ 15 x (15 – 9) x (15 – 8) x (15 – 13) = 35.49 m²

Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD

= (35.496 + 30) m² = 65.5m².

问题5.梯形的两个平行边分别为60 m和77 m，另一边分别为25 m和26 m。找到梯形的面积?

解决方案：

Given that,

Two parallel sides of trapezium are AB = 77 m and CD = 60 m

The other two parallel sides of trapezium are BC = 26 m, AD = 25m

DE is perpendicular to AB and also, CF is perpendicular to AB

Therefore, DC = EF = 60 m

Let AE = x

therefore, BF = 77 – 60 – x

BF = 17 – x

In triangle ADE,

By using Pythagoras theorem,

DE² = AD² − AE²

DE² = 25² − x²

In triangle BCF,

By using Pythagoras theorem,

CF² = BC² − BF²

CF² = 26² − (17 − x)²

Here, DE = CF

therefore, DE² = CF²

25² − x² = 26² − (17 − x)²

25² − x² = 26² − (17² − 34x + x²)

25² − x² = 26² − 17² + 34x + x²

25² = 26² − 17² + 34x

x = 7

DE² = 25² − x²

DE = √625 – 49

DE = 24 m

Area of trapezium = 1/2 × (60 + 77) × 24

Hence, Area of trapezium = 1644 m²

问题6：找到一个菱形的区域，该区域的周长为80 m，其中一个对角线为24 m。

解决方案：

Given that,

Perimeter of a rhombus = 80 m and AC = 24 m

As we know that, Perimeter of a rhombus = 4 × side = 4 × a

4 × a = 80 m

a = 20 m

OA = 1/2 × AC

OA = 12 m

In triangle AOB,

OB² = AB² − OA²

OB² = 20² − 12²

OB = 16 m

Also, OB = OD because diagonal of rhombus bisect each other at 90°

Therefore, BD = 2 OB = 2 × 16 = 32 m

Area of rhombus = 1/2 × BD × AC

Area of rhombus = 1/2 × 32 × 24

Area of rhombus = 384 m²

问题7.一块两侧长为32 m，对角线长为10 m的菱形板，以每平方米5卢比的比率被涂漆。查找绘画成本。

解决方案：

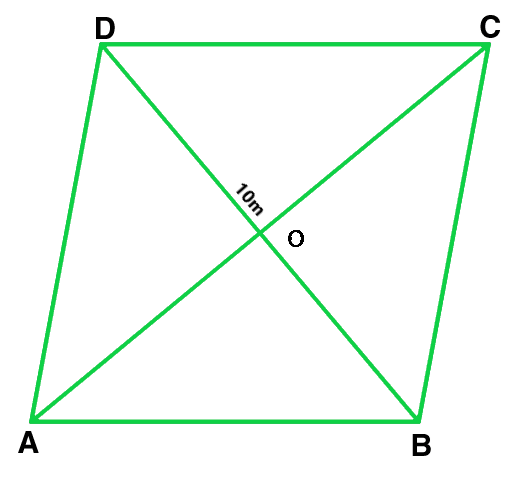
Given that,

Perimeter of a rhombus = 32 m

As we know that, Perimeter of a rhombus = 4 × side

4 × side = 32 m

4 × a = 32 m

a = 8 m

AC = 10 m                     (Given)

OA = 12 × AC

OA = 12 × 10 = 5 m

By using Pythagoras theorem,

OB² = AB² − OA²

OB² = 8² − 5²

OB = √39 m

BD = 2 × OB

BD = 2√39 m

Area of the sheet = 1/2 × BD × AC

Area of the sheet = 1/2 ×2√39 × 10

Therefore, cost of printing on both sides at the rate of Rs. 5 per m²

= Rs 2 × 10√39 × 5 = Rs. 625

问题8.找到四边形ABCD的面积，其中AD = 24 cm，角度BAD = 90°，BCD形成等边三角形，其每边等于26 cm。 [取√3= 1.73]

解决方案：

Given that, in a quadrilateral ABCD in which AD = 24 cm,

Angle BAD = 90°,

BCD is an equilateral triangle and the sides BC = CD = BD = 26 cm.

In triangle BAD, by applying Pythagoras theorem,

BA² = BD² − AD²

BA² = 26² + 24²

BA = √100 = 10 cm

Area of the triangle BAD = 1/2 × BA × AD

= 1/2 × 10 × 24 = 120 cm²

Area of the equilateral triangle = √3/4 × side

Area of the equilateral triangle QRS = √3/4 × 26

Area of the equilateral triangle BCD = 292.37 cm²

Therefore, the area of quadrilateral ABCD = Area of triangle BAD + Area of the triangle BCD

The area of quadrilateral ABCD = 120 + 292.37 = 412.37 cm²

问题9.找到四边形ABCD的面积，其中AB = 42 cm，BC = 21 cm，CD = 29 cm，DA = 34 cm，对角线BD = 20 cm。

解决方案：

Given that,

AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm, and the diagonal BD = 20 cm.

Now, for the area of triangle ABD,

Perimeter of triangle ABD 2s = AB + BD + DA

2s = 34 cm + 42 cm + 20 cm

s = 48 cm

By using Heron’s Formula,

Area of triangle ABD = √s x (s – a) x (s – b) x (s – c)

= √ 48 x (48 – 42) x (48 – 20) x (48 – 34) = 33 6cm²

Now, for the area of triangle BCD,

Perimeter of triangle BCD 2s = BC + CD + BD

2s = 29cm + 21cm + 20cm

s = 35 cm

By using Heron’s Formula,

Area of triangle BCD = √s x (s – a) x (s – b) x (s – c)

= √ 35 x (14) x (6) x (15) = 210 cm²

Therefore, Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD

Area of quadrilateral ABCD = 336 + 210

Area of quadrilateral ABCD = 546 cm²

问题10.找到四边形ABCD的周长和面积，其中AB = 17 cm，AD = 9 cm，CD = 12 cm，AC = 15 cm，角度ACB = 90°。

解决方案：

Given that,

The sides of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, AC = 15 cm and an angle ACB = 90°

By using Pythagoras theorem,

BC² = AB² − AC²

BC² = 17² − 15²

BC = 8 cm

Now, area of triangle ABC = ½ × AC × BC

= 1/2 × 8 × 15 = 60 cm²

Now, for the area of triangle ACD

Perimeter of triangle ACD 2s = AC + CD + AD

2s = 15 + 12 + 9

s = 18 cm

By using Heron’s Formula,

Area of triangle ACD = √s x (s – a) x (s – b) x (s – c)

= √ 18 x (3) x (6) x (9) = 54 cm²

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD

= 60 cm² + 54 cm²

Hence, Area of quadrilateral ABCD = 114 cm²

问题11：平行四边形ABCD的相邻边长分别为34 cm和20 cm，对角AC边长为42 cm。找到平行四边形的面积。

解决方案：

Given that,

The adjacent sides of a parallelogram ABCD measures 34 cm and 20 cm, and the diagonal AC measures 42 cm.

Area of the parallelogram = Area of triangle ADC + Area of triangle ABC

As we know that, Diagonal of a parallelogram divides into two congruent triangles

Therefore, Area of the parallelogram = 2 × (Area of triangle ABC)

Now, for area of triangle ABC

Perimeter = 2s = AB + BC + CA

2s = 34 cm + 20 cm + 42 cm

s = 48 cm

By using Heron’s Formula,

Area of triangle ABC = √s x (s – a) x (s – b) x (s – c)

= √ 48 x (14) x (28) x (6) = 336 cm²

Therefore, area of parallelogram ABCD = 2 × (Area of triangle ABC)

Area of parallelogram = 2 × 336 cm²

Hence, Area of parallelogram ABCD = 672 cm²

问题12.找到下图所示的电磁罗盘的刀片区域：

解决方案：

From the figure we conclude that, Area of the blades of magnetic compass = Area of triangle ADB + Area of triangle CDB

Now, for the area of triangle ADB,

Perimeter = 2s = AD + DB + BA

2s = 5 cm + 1 cm + 5 cm

s = 5.5 cm

By using Heron’s Formula,

Area of triangle DEF = √s x (s – a) x (s – b) x (s – c)

= √ 5.5 x (0.5) x (4.5) x (0.5) = 2.49 cm²

Also, area of triangle ADB = Area of triangle CDB

Therefore, area of the blades of the magnetic compass = 2 × area of triangle ADB

Area of the blades of the magnetic compass = 2 × 2.49

Hence, Area of the blades of the magnetic compass = 4.98 cm²

问题13。如图所示，通过将10种相等大小的两种不同类型的纸张的三角条粘在一起制成一个手扇。等长条的尺寸为25厘米，25厘米和14厘米。找到制作手扇所需的每种纸张的面积。

解决方案：

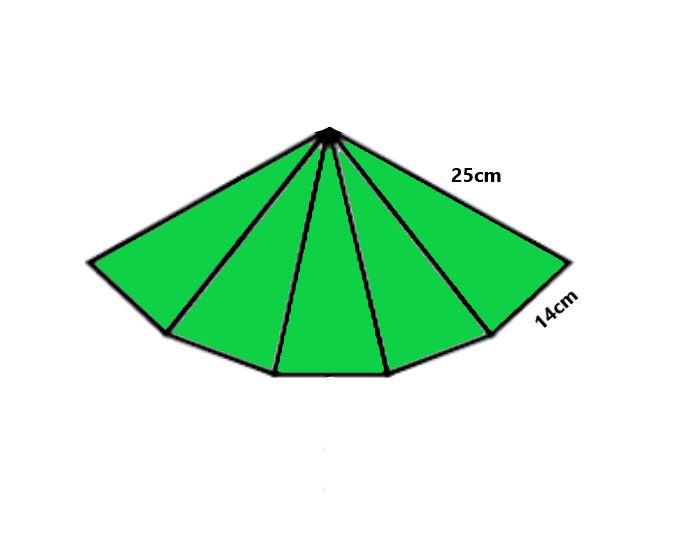
Given that,

The sides of AOB,

AO = 25 cm,

OB = 25 cm,

BA = 14 cm.

Area of each strip = Area of triangle AOB

Now, for the area of triangle AOB

Perimeter = AO + OB + BA

2s = 25 cm +25 cm + 14 cm

s = 32 cm

By using Heron’s Formula,

Area of triangle AOB = √s x (s – a) x (s – b) x (s – c)

= √ 32 x (7) x (4) x (18) = 168 cm²

Also, area of each type of paper needed to make a fan = 5 × Area of triangle AOB

Area of each type of paper needed to make a fan = 5 × 168 cm²

Area of each type of paper needed to make a fan = 840 cm²

问题14.一个三角形和一个平行四边形具有相同的底和相同的面积。如果三角形的边分别为13 cm，14 cm和15 cm，并且平行四边形位于底部14 cm上，请找到平行四边形的高度。

解决方案：

Given that,

DC = 15 cm,

CE = 13 cm,

ED = 14 cm.

Let’s assume that the h be the height of parallelogram ABCD,

Now, for the area of triangle DCE.

Perimeter = DC + CE + ED

2s = 15 cm + 13 cm + 14 cm

s = 21 cm

By using Heron’s Formula,

Area of triangle AOB = √s x (s – a) x (s – b) x (s – c)

= √ 21 x (7) x (8) x (6) = 84 cm²

Also, area of triangle DCE = Area of parallelogram ABCD = 84 cm²

24 × h = 84 cm²

h = 6 cm.