第12类RD Sharma解决方案–第6章行列式–练习6.5

问题1.解决以下齐次线性方程组的每个系统：

x + y – 2z = 0

2x + y – 3z = 0

5x + 4y – 9z = 0

解决方案：

Given: 

x + y – 2z = 0

2x + y – 3z =0

5x + 4y – 9z = 0

This system of equations can be expressed in the form of a matrix AX = B

Now find the determinant,

$D=\begin{vmatrix}1&1&-2\\2&1&-3\\5&4&-9\end{vmatrix}\\ |A|=1\begin{vmatrix}1&-3\\4&-9\end{vmatrix}-1\begin{vmatrix}2&-3\\5&-9\end{vmatrix}-2\begin{vmatrix}2&1\\5&4\end{vmatrix}$

= 1(1 × (-9) – 4 × (-3)) – 1(2 × (-9) – 5 × (-3)) – 2(4 × 2 – 5 × 1)

= 1(-9 + 12) – 1(-18 + 15) – 2(8 – 5)

= 1 × 3 – 1 × (-3) – 2 × 3

= 3 + 3 – 6

= 0

So, D = 0, that means this system of equations has infinite solution.

Now, 

Let z = k

⇒ x + y = 2k

And 2x + y = 3k

Now using the Cramer’s rule

x = $\frac{D_1}{D}$

x = $\frac{\begin{vmatrix}2k&1\\3k&1\end{vmatrix}}{\begin{vmatrix}1&1\\2&1\end{vmatrix}}$

x = $\frac{-k}{-1}$

x = k

Similarly,

y = $\frac{D_2}{D}$

y = $\frac{\begin{vmatrix}1&2k\\2&3k\end{vmatrix}}{\begin{vmatrix}1&1\\2&1\end{vmatrix}}$

y = $\frac{-k}{-1}$

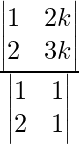
y = k

Therefore,

x = y = z = k.

问题2.求解以下每个齐次线性方程组：

2x + 3y + 4z = 0

x + y + z = 0

2x + 5y – 2z = 0

解决方案：

2x + 3y + 4z = 0

x + y + z = 0

2x + 5y – 2z = 0

This system of equations can be expressed in the form of a matrix AX = B

Find the determinant

$D = \begin{vmatrix}2&3&4\\1&1&1\\2&5&-2\end{vmatrix}\\ |A|=2\begin{vmatrix}1&1\\5&-2\end{vmatrix}-3\begin{vmatrix}1&1\\2&-2\end{vmatrix}+4\begin{vmatrix}1&1\\2&5\end{vmatrix}$

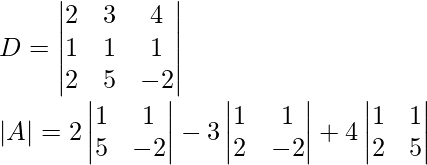
= 2(1 × (-2) – 1 × 5) – 3(1 × (-2) – 2 × 1) + 4(1 × 5 – 2 × 1)

= 2(-2 – 5) – 3(-2 – 2) + 4(5 – 2)

= 2 × (-7) – 3 × (-4) + 4 × 3

= -14 + 12 + 12

= -10

Hence, D ≠ 0, so the system of equation has trivial solution.

Therefore, the system of equation has only solution as x = y = z = 0.

问题3：求解以下每个齐次线性方程组：

3x + y + z = 0

x – 4y + 3z = 0

2x + 5y – 2z = 0

解决方案：

Given:

3x + y + z = 0

x – 4y + 3z = 0

2x +5y – 2z = 0

This system of equations can be expressed in the form of a matrix AX = B

Find the determinant

$D =\begin{vmatrix}3&1&1\\1&-4&3\\2&5&-2\end{vmatrix}$

= 3(8 – 15) – 1(-2 – 6) + 1(13)

= -21 + 8 + 13

= 0

So, the system has infinite solutions:

Let z = k,

So, 

3x + y = -k

x – 4y = -3k

Now,

x = 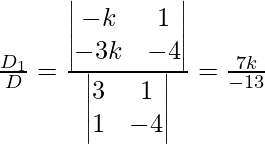$\frac{D_1}{D}=\frac{\begin{vmatrix}-k&1\\-3k&-4\end{vmatrix}}{\begin{vmatrix}3&1\\1&-4\end{vmatrix}}=\frac{7k}{-13}$    

y = 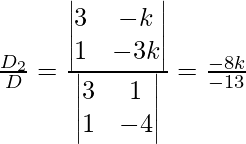$\frac{D_2}{D}=\frac{\begin{vmatrix}3&-k\\1&-3k\end{vmatrix}}{\begin{vmatrix}3&1\\1&-4\end{vmatrix}}=\frac{-8k}{-13}$

x = $\frac{-7k}{13}$

y = $\frac{8k}{13}$

z = k

and there values satisfy equation 3

Hence, x = -7k, y = 8k, z = 13k

问题4.找到以下线性方程组具有非平凡解的λ的实数值

2λx– 2y + 3z = 0

x +λy+ 2z = 0

2x +λz= 0

解决方案：

Finding the determinant

$D=\begin{vmatrix}2λ &-2&3\\1&λ &2\\2&0&λ \end{vmatrix}$ 

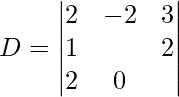
= 3λ³ + 2λ – 8 – 6λ 

= 2λ³ – 4λ – 8

Which is satisfied by λ = 2 {for non-trival solutions λ =2}

Now let z = k

4x – 2y = -3k

x + 2y = -3k

x = 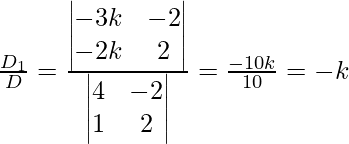$\frac{D_1}{D}=\frac{\begin{vmatrix}-3k&-2\\-2k&2\end{vmatrix}}{\begin{vmatrix}4&-2\\1&2\end{vmatrix}}=\frac{-10k}{10}=-k$    

y =$\frac{D_2}{D}=\frac{\begin{vmatrix}4&-3k\\1&-2k\end{vmatrix}}{\begin{vmatrix}4&-2\\1&2\end{vmatrix}}=\frac{-5k}{10}=\frac{-k}{2}$

Hence, the solution is x = -k, y = $\frac{-k}{2}$, z = k

问题5：如果a，b，c是非零实数，并且方程组是

(a – 1)x = y + z

(b – 1)y = z + x

(c – 1)z = x + y

有一个非平凡的解，则证明ab + bc + ca = abc

解决方案：

Finding the determinant

$D=\begin{vmatrix}(a-1)&-1&-1\\-1&(b-1)&-1\\-1&-1&(c-1)\end{vmatrix}$

Now for non-trivial solution, D = 0

0 = (a – 1)[(b – 1)(c – 1) – 1]+1[-c + 1 – 1] + [-c + 1 – 1] – [ 1 + b – 1]

0 = (a – 1)[bc – b – c + 1 – 1] – c – b

0 = abc – ab -ac + b + c – c – b

ab + bc + ac = abc

Hence proved