第12类RD Sharma解决方案–第6章行列式–练习6.3

问题1.找到在点处具有顶点的三角形的面积：

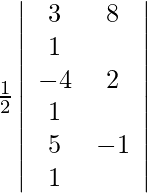
(i)(3，8)，(− 4，2)和(5，-1)

解决方案：

Given (3, 8), (−4, 2) and (5, −1) are the vertices of the triangle. 

We know that, if vertices of a triangle are (x₁, y₁), (x₂, y₂) and (x₃, y₃), then the area of the triangle is given by,

A = 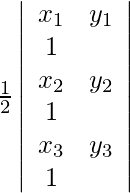$\frac{1}{2} \left| \begin{array}{cc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} \right|$

= $\frac{1}{2} \left| \begin{array}{cc} 3 & 8 & 1 \\ -4 & 2 & 1 \\ 5 & -1 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[3(2+1)-8(-4-5)+1(4-10)]$

= $\frac{1}{2}[9+72-6]$

= $\frac{75}{2}$

Therefore, area of the triangle is $\frac{75}{2}$ sq. units.

(ii)(2、7)，(1、1)和(10、8)

解决方案：

Given (2, 7), (1, 1) and (10, 8) are the vertices of the triangle.

The area of the triangle is given by,

A = 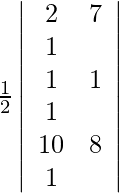$\frac{1}{2} \left| \begin{array}{cc} 2 & 7 & 1 \\ 1 & 1 & 1 \\ 10 & 8 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[2(1-8)-7(1-10)+1(8-10)]$

= $\frac{1}{2}[-14+63-2]$

= $\frac{47}{2}$

Therefore, area of the triangle is $\frac{47}{2}$ sq. units.

(iii)(-1，-8)，(-2，-3)和(3、2)

解决方案：

Given (−1, −8), (−2, −3) and (3, 2) are the vertices of the triangle.

The area of the triangle is given by,

A = 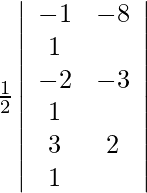$\frac{1}{2} \left| \begin{array}{cc} -1 & -8 & 1 \\ -2 & -3 & 1 \\ 3 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|-1(-3-2)+8(-2-3)+1(-4+9)|$

= $\frac{1}{2}|5-40+5|$

= $\frac{30}{2}$

= 15

Therefore, area of the triangle is 15 sq. units.

(iv)(0，0)，(6，0)，(4，3)

解决方案：

Given (0, 0), (6, 0), (4, 3) are the vertices of the triangle.

The area of the triangle is given by,

A = $\frac{1}{2} \left| \begin{array}{cc} 0 & 0 & 1 \\ 6 & 0 & 1 \\ 4 & 3 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[0-0+1(18-0)]$

= $\frac{18}{2}$

= 9

Therefore, area of the triangle is 9 sq. units.

问题2。使用行列式表明以下几点是共线的：

(i)(5、5)，(− 5、1)和(10、7)

解决方案：

Given points are (5, 5), (−5, 1) and (10, 7).

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

A = 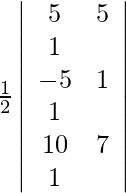$\frac{1}{2} \left| \begin{array}{cc} 5 & 5 & 1 \\ -5 & 1 & 1 \\ 10 & 7 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[5(1-7)-5(-5-10)+1(-35-10)]$

= $\frac{1}{2}[-30+75-45]$

= 0

As the area of the triangle is 0, the points are collinear.

Hence proved.

(ii)(1，-1)，(2，1)和(4，5)

解决方案：

Given points are (1, −1), (2, 1) and (10, 8).

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

A = $\frac{1}{2} \left| \begin{array}{cc} 1 & -1 & 1 \\ 2 & 1 & 1 \\ 4 & 5 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[1(1-5)+1(2-4)+1(10-4)]$

= $\frac{1}{2}[-4-2+6]$

= 0

As the area of the triangle is 0, the points are collinear.

Hence proved.

(iii)(3，-2)，(8，8)和(5，2)

解决方案：

Given points are (3, −2), (8, 8) and (5, 2).

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

A = 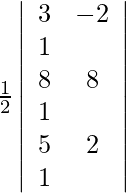$\frac{1}{2} \left| \begin{array}{cc} 3 & -2 & 1 \\ 8 & 8 & 1 \\ 5 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[3(8-2)+2(8-5)+1(16-40)]$

= $\frac{1}{2}[18+6-24]$

= 0

As the area of the triangle is 0, the points are collinear.

Hence proved.

(iv)(2、3)，(-1，-2)和(5、8)

解决方案：

Given points are (2, 3), (−1, −2) and (5, 8).

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

A = 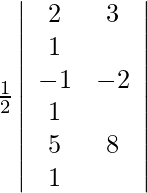$\frac{1}{2} \left| \begin{array}{cc} 2 & 3 & 1 \\ -1 & -2 & 1 \\ 5 & 8 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[2(-2-8)-3(-1-5)+1(-8+10)]$

= $\frac{1}{2}[-20+18+2]$

= 0

As the area of the triangle is 0, the points are collinear.

Hence proved.

问题3.如果点(a，0)，(0，b)和(1，1)是共线的，则证明a + b = ab。

解决方案：

Given points (a, 0), (0, b) and (1, 1) are collinear.

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

=> $\frac{1}{2} \left| \begin{array}{cc} a & 0 & 1 \\ 0 & b & 1 \\ 1 & 1 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[a(b-1)-0+1(0-b)]=0$

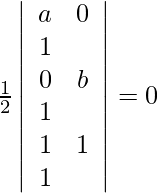
=> ab − a − b = 0

=> a + b = ab

Hence proved.

问题4.使用行列式证明，如果ab’= a’b，则点(a，b)，(a’，b’)和(a – a’，b – b)是共线的。

解决方案：

Given points are (a, b), (a’, b’) and (a – a’, b – b) and a b’ = a’ b.

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

=> $\frac{1}{2} \left| \begin{array}{cc} a & b & 1 \\ a' & b' & 1 \\ a - a' & b - b' & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[a(b'-b+b')-b(a'-a+a')+1(a'b-a'b'-ab'+a'b')]=0$

=> $\frac{1}{2}[ab'-ab+ab'-a'b+ab-a'b+a'b-ab')]=0$

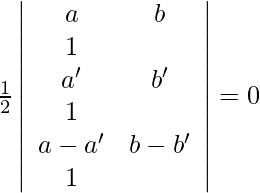
=> a b’ − a’ b = 0

=> a b’ = a’ b

Hence proved.

问题5.找到λ的值，以使点(1，-5)，(− 4，5)和(λ，7)共线。

解决方案：

Given points are (1, −5), (−4, 5) and (λ, 7).

For these points to be collinear, the area of the triangle they form must be zero. So, we get,

=> $\frac{1}{2} \left| \begin{array}{cc} 1 & -5 & 1 \\ -4 & 5 & 1 \\ λ & 7 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[1(5-7)+5(-4-λ)+1(-28-5λ)]=0$

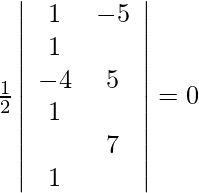
=> −2 − 20 − 5λ − 28 − 5λ = 0

=> 10λ = 50

=> λ = 5

Therefore, the value of λ is 5.

问题6.如果∆的面积为35平方厘米，且顶点分别为(x，4)，(2，-6)和( 5，4)，则求x的值。

解决方案：

Given points are (x, 4), (2, −6) and (5, 4).

We know that, if vertices of a triangle are (x₁, y₁), (x₂, y₂) and (x₃, y₃), then the area of the triangle is given by,

A = $\frac{1}{2} \left| \begin{array}{cc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} \right|$

=> $\frac{1}{2} \left| \begin{array}{cc} x & 4 & 1 \\ 2 & -6 & 1 \\ 5 & 4 & 1 \\ \end{array} \right| = 35$

=> $\left| \begin{array}{cc} x & 4 & 1 \\ 2 & -6 & 1 \\ 5 & 4 & 1 \\ \end{array} \right| = \pm70$

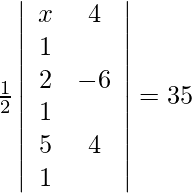
=> − 10x + 12 + 38 = ±70

=> – 10x + 50 = ±70

Taking positive sign, we get

=> – 10x + 50 = 70

=> 10x = – 20

=> x = – 2

Taking negative sign, we get

=> – 10x + 50 = – 70

=> 10x = 120

=> x = 12

Therefore, the value of x is 12 or –2.

问题7.使用行列式，找到顶点为(1、4)，(2、3)，(– 5，–3)的三角形的面积。给定的点是共线的吗?

解决方案：

Given points are (1, 4), (2, 3), (–5, –3).

So, area = $\frac{1}{2} \left| \begin{array}{cc} 1 & 4 & 1 \\ 2 & 3 & 1 \\ -5 & -3 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|1(3+3)-4(2+5)+1(-6+15)|$

= $\frac{1}{2}|6-28+9|$

= $\frac{13}{2}$

As the area of the triangle formed by these three points is not zero, the points are not collinear.

问题8.使用行列式，找到顶点为(–3，5)，(3，–6)，(7，2)的三角形的面积。

Given points are (–3, 5), (3, –6), (7, 2).

So, area = 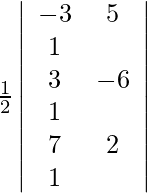$\frac{1}{2} \left| \begin{array}{cc} -3 & 5 & 1 \\ 3 & -6 & 1 \\ 7 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|-3(-6-2)-5(3-7)+1(6+42)|$

= $\frac{1}{2}|24+20+48|$

= $\frac{92}{2}$

= 46

Therefore, the area of the triangle is 46 sq. units.

问题9。使用行列式求k的值，以使点(k，2–2k)，(–k + 1，2k)，(–4–k，6–2k)可以共线。

解决方案：

Given points are (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k). As the points are collinear, the area must be 0.

=> $\frac{1}{2} \left| \begin{array}{cc} k & 2-2k & 1 \\ -k+1 & 2k & 1 \\ -4-k & 6-2k & 1 \\ \end{array} \right|=0$

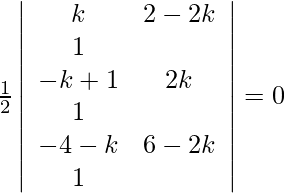
=> k(2k – 6 + 2k) – (2–2k) (–k + 1 + 4 + k) + [(1–k) (6–2k) – 2k (–4–k)] = 0

=> 8k² + 4k – 4 = 0

=> 8k² + 8k – 4k – 4 = 0

=> 8k (k+1) – 4 (k+1) = 0

=> 8k = 4 or k = –1

=> k = 1/2 or k = –1

Therefore, the value of k is 1/2 or –1.

问题10.如果点(x，–2)，(5、2)，(8、8)是共线的，则使用行列式求x。

解决方案：

Given points are (x, –2), (5, 2), (8, 8). As the points are collinear, the area must be 0.

=> $\frac{1}{2} \left| \begin{array}{cc} x & -2 & 1 \\ 5 & 2 & 1 \\ 8 & 8 & 1 \\ \end{array} \right|=0$

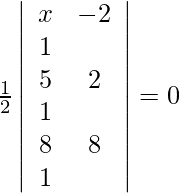
=> x(2 – 8) + 2(5 – 8) + 1(40–16) = 0

=> –6x – 6 + 24 = 0

=> 6x = 18

=> x = 3

Therefore, the value of x is 3.

问题11.如果点(3，–2)，(x，2)，(8，8)是共线的，请使用行列式求x。

解决方案：

Given points are (3, –2), (x, 2), (8, 8). As the points are collinear, the area must be 0.

=> $\frac{1}{2} \left| \begin{array}{cc} 3 & -2 & 1 \\ x & 2 & 1 \\ 8 & 8 & 1 \\ \end{array} \right|=0$

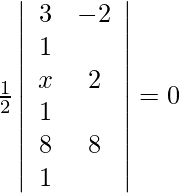
=> 3(2 – 8) + 2(x – 8) + 1(8x–16) = 0

=> –18 + 2x – 16 + 8x – 16 = 0

=> 10x = 50

=> x = 5

Therefore, the value of x is 5.

问题12：使用行列式，找到以下方程式

(i)连接点(1、2)和(3、6)的线。

解决方案：

Let (x, y), (1, 2), (3, 6) be the points on the line. As these points are collinear, we get,

=> $\frac{1}{2} \left| \begin{array}{cc} x & y & 1 \\ 1 & 2 & 1 \\ 3 & 6 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[x(2-6)-y(1-3)+1(6-6)]=0$

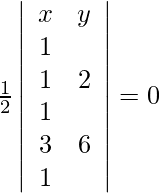
=> −4x + 2y = 0

=> 2x − y = 0

Therefore, the required equation is 2x − y = 0.

(ii)连接点(3，1)和(9，3)的线。

解决方案：

Let (x, y), (3, 1), (9, 3) be the points on the line. As these points are collinear, we get,

=> $\frac{1}{2} \left| \begin{array}{cc} x & y & 1 \\ 3 & 1 & 1 \\ 9 & 3 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[x(1-3)-y(3-6)+1(9-9)]=0$

=> −2x + 6y = 0

=> x − 3y = 0

Therefore, the required equation is x − 3y = 0.

问题13.找到k的值

(i)如果顶点为(k，0)(4，0)(0，2)的三角形的面积为4平方单位。

解决方案：

Given points are (k, 0) (4, 0) (0, 2). According to the question, we have,

=> $\frac{1}{2} \left| \begin{array}{cc} k & 0 & 1 \\ 4 & 0 & 1 \\ 0 & 2 & 1 \\ \end{array} \right|=4$

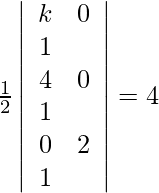
=> |k(0−2) − 0 + 1(8−0)| = 8

=> −2k + 8 = ±8

=> −2k + 8 = 8 or −2k + 8 = −8

=> k = 0 or k = 8

Therefore, the value of k is 0 or 8.

(ii)顶点为(−2，0)(0，4)(0，k)的三角形的面积是否为4平方单位。

解决方案：

Given points are (−2, 0) (0, 4) (0, k). According to the question, we have,

=> $\frac{1}{2} \left| \begin{array}{cc} -2 & 0 & 1 \\ 0 & 4 & 1 \\ 0 & k & 1 \\ \end{array} \right|=4$

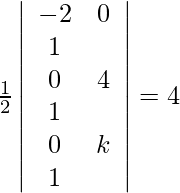
=> |−2(4−k) − 0 + 1(0)| = 8

=> −8 + 2k = ±8

=> −8 + 2k = 8 or −8 + 2k = −8

=> k = 8 or k = 0

Therefore, the value of k is 0 or 8.