无理数

我们通常研究并且到目前为止一直关注的数字是用于计数的正整数1,2,3，依此类推。这些被称为自然数，已经存在了数千年。

著名的数学家克罗内克(Kronecker)曾说过：

“God created the natural numbers; all the rest is the work of man.”

然后，生活的基本必需品导致了诸如3 / 4、1 / 5等分数的产生。这些数字称为有理数。

Note: These numbers are not called rational numbers because they are “reasonable”, they are called rational because they are ratios of whole numbers. 

所有这些数字都可以表示在数字行中的特定位置。

但是大约2500年前，希腊人在研究几何学时发现了其他东西。他们惊讶地发现有些数字无法表示为比率整数。

例如：

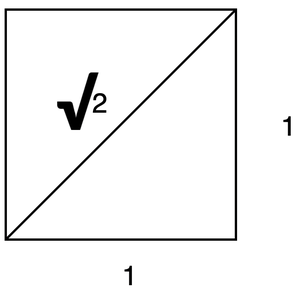
他们注意到，边长单位为1的平方。对角线的长度不能用任何比例的整数表示。

用现代数学术语来说，这样的数字称为无理数。从几何学上讲，这意味着不存在公共单位(但是可能很小)，因此正方形的边和对角线是其整数倍。类似地，圆的周长是直径的无理倍数。该倍数是“ pi”。

现在让我们正式定义有理数和无理数。

有理数

如果数字“ x”可以以“ p / q”的形式书写，则其中p和q是整数(q≠0)，则它是有理数。

示例：25是有理数。如何? 25可以写成$\frac{25}{1}$其中p = 25且q =1。类似地，5.5也是有理数，可以表示为$\frac{11}{2}$等等。

无理数

如果不能以“ p / q”的形式写入数字“ x”，则称其为“无理数”，其中p和q为整数(q≠0)。就像有无限多个有理数一样，也有无限多个无理数。

例如： √2，√3， $\pi$

√2= 1.41421356237309504880…

$\pi$ = 3.14159265358979323846264338327950…

识别不合理数字的另一个提示是小数继续而不重复。

热门非理性数字：

• Pi ， π = 3.14159265358979323846264338327950…。这是一个非常有名的非理性数字。人们已经计算出其值，直到小数点后四舍五入，但仍未找到任何模式。
• 欧拉数“ e” 。它在数学中也很受欢迎。同样，在这种情况下，人们尝试计算最多十进制数，但仍未找到任何模式。 e = 2.7182818284590452353602874713527(以及更多…)。
• 黄金比例。这是在计算机科学，设计，艺术，建筑等许多领域中发现的非理性数字。

√2是无理数吗?

Proof:

To begin with, let’s suppose it is a Rational Number

Since it is Rational, It can be represented in the most simplified form P/Q where P/Q are Integers (Q≠ 0) and P/Q can not be further simplified,

Which means that the fraction P/Q is irreducible.

                                                       P/Q = √2

 Squaring both Sides:

                                                      (P/Q)² = 2

                                                       P²/Q² = 2

                                                       P² = 2 Q²

Here, It is clear that P² is divisible by 2. Therefore, P² is an Even Number.

Since, P² is Even, P has to be an Even number too.

Therefore, P can be written as 2A as it is divisible by 2.

By putting the value P = 2A, we will get:

                                                       (2A)² = 2Q²

                                                                            4A² = 2Q²

                                                               2A² = Q²

Here, It is observed that Q² is also an Even number as it is divisible by 2.

Since Q² is Even, Q has to be Even too. Therefore, Both P and Q turned out to be Even numbers, which means they can be Simplified further.

It is a Contradiction as it was already defined to be a fraction in its simplest form.

Therefore, √2 cannot be Rational, It is an Irrational number.

无理数的性质

无理数和有理数的加法：

The addition of an irrational and a rational number always gives an irrational number. 

For example, it’s known that √2 = 1.41421356237309504880… Now √2 + 1 = 2.41421356237309504880…. This is still irrational. 

无理数与非零有理数的乘积。

Multiplication of any irrational number with any nonzero rational number results in an irrational number. 

Proof: Let x be an irrational number and y be a non-zero rational number. 

We want to know if z = xy is irrational or rational ? 

This will be proved by contradiction. Let’s assume z is rational number. 

If z is rational, then x = z/y where both z and y are rational number. This makes x as rational number. This is a contradiction, which means that the previous assumption was wrong. So, z will always be irrational number. 

两个无理数的乘积：

When multiplying a rational number, it is not necessary that the resulting number is always irrational. 

• π × π = π² is irrational.
• But √2 × √2 = 2 is rational.

两个无理数之和：

The answer to this is also similar to the above property. The Sum of two irrational numbers is sometimes rational sometimes irrational.  

• 3√2 + 4√3 is irrational.
• (3√2 + 6) + (- 3√2) = 6, this is rational.

Fun Fact: Apparently Hippasus (one of Pythagoras’ students) discovered irrational numbers when trying to write the square root of 2 as a fraction (using geometry, it is thought). Instead, he proved the square root of 2 could not be written as a fraction, so it is irrational.

But followers of Pythagoras could not accept the existence of irrational numbers, and it is said that Hippasus was drowned at sea as a punishment from the gods!

Pi之谜

让我们围成一个圆圈，测量其周长，然后将其除以直径。如果精确测量，它将始终是一个常数。

这个恒定比率用希腊符号表示$\pi$ (读为pi)。那是，

$\frac{circumference}{diameter} = \pi \\$

它是一个重要的普遍常数，它存在于我们宇宙和日常生活的许多地方。它不是人类创造的，而是被发现的。我们发现发生pi的地方之一是几何。

那么， Pi的价值是什么?

π= 3.14159265358979323846264338327950…

它不是无限的，它是一个无理数。

Note: We often take $\frac{22}{7}$ as value of Pi, but it is an approximation. 

现在人们可能会认为，理性是非理性的吗?一个可以测量周长，一个可以测量直径，然后取它们的比率。因此它必须是理性的。

实际上，如果对直径进行测量并且是合理的，那么任何人都不会遇到这种情况。那么圆周必须是非理性的，反之亦然。因此，无论是直径还是周长。其中之一永远是不理性的。通常，测量仪器不够精确。如果存在一个完美的量表，它将表明该分数中的至少一个数字是不合理的。

关于无理数的一些样本问题

问题1：这些数字是否属于非理性数字类别：5、3.45、4.444444…，√9。

回答：

These numbers mentioned above are not Irrational number.

• 5 is a Whole number and therefore, is Rational
• 3.45 is a number with Terminating Decimal and therefore, it is Rational too.
• 4.444444… is a Number with Repeating Decimal Expansion, It is Rational.
• √9 is 3 i.e; the square root of 9 is 3 and 3 is a Whole number. Therefore, √9 is Rational.

问题2： “每个实数都是一个无理数”。对或错?

答：

False, All numbers are real numbers and all non-terminating real numbers are irrational number. For example 2, 3, 4, etc. are some example of real numbers and these are not irrational.

问题3：确定以下数字是有理数还是无理数。

√3，74，8.432432432 …，3.14159265358979 …，√11，55/5。

答：

74, 8.432432432…, and 55/5(11) are Rational numbers as either they are Integers or their decimal expansions are terminating, repeating.

√3, 3.14159265358979…, and √11 are Irrational numbers as their decimal Expansions are Non-terminating, Non-repeating.

问题4 ：为什么整数不是无理数?

答：

Integers (Either Positive, Negative or Zero) are not Irrational but Rational numbers since they can be represented in the simplest fraction form P/Q (where Q ≠ 0).