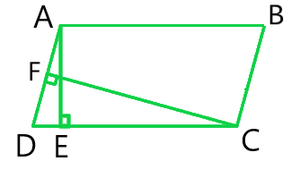
问题1:在给定的图中,ABCD是平行四边形,AE⊥DC和CF⊥AD。如果AB = 16厘米,AE = 8厘米,CF = 10厘米,找到AD吗?
解决方案:
As Given in the Question,
AB = CD = 16 cm (Opposite sides of a parallelogram)
CF = 10 cm and AE = 8 cm
Now, As we have studied in this Chapter we know,
Area of Parallelogram = Base x Altitude
⇒ CD × AE = AD × CF
⇒ 16 × 8 = AD × 10
⇒ AD = 128/10 cm
⇒ AD = 12.8 cm
问题2:如果E,F,G和H分别是平行四边形ABCD的边的中点,则表明ar(EFGH)= 1/2 ar(ABCD)?
解决方案:
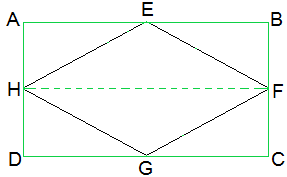
As Given in the Question ,
E, F, G and H are the mid-points of the sides of a parallelogram ABCD respectively.
To Prove,
ar (EFGH) = ½ ar(ABCD)
First, we have to do some construction
join H to E
Proof:
As we know,
AD || BC and AD = BC (Opposite sides of a parallelogram)
⇒ ½ AD = ½ BC
As H and F are the mid points of AD and BC
AH || BF and and DH || CF
Therefore,
AH = BF and DH = CF (H and F are mid points)
∴ ABFH and HFCD are parallelograms.
As we know that, ΔEFH and parallelogram ABFH, both lie on the same base FH and ΔEFH lie in-between the same parallel lines AB and HF.
Therefore,
Area of EFH = ½ Area of ABFH — (i)
And, Area of GHF = ½ Area of HFCD — (ii)
Now, Adding (i) and (ii) we get,
Area of ΔEFH + Area of ΔGHF = ½ Area of ABFH + ½ Area of HFCD
⇒ Area of EFGH = Area of ABFH
∴ ar (EFGH) = ½ ar(ABCD)
问题3:P和Q是分别位于平行四边形ABCD的DC和AD边的任意两个点。证明ar(APB)= ar(BQC)?
解决方案:
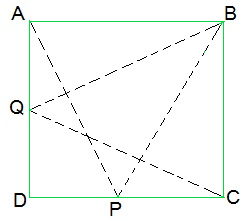
ΔAPB and parallelogram ABCD lie on the same base AB and ΔAPB lie in-between same parallel AB and DC.
Now, As we know that
ar(ΔAPB) = ½ ar(parallelogram ABCD) — (i)
Similarly,
ar(ΔBQC) = ½ ar(parallelogram ABCD) — (ii)
From (i) and (ii), we have
ar(ΔAPB) = ar(ΔBQC)
Hence proved,
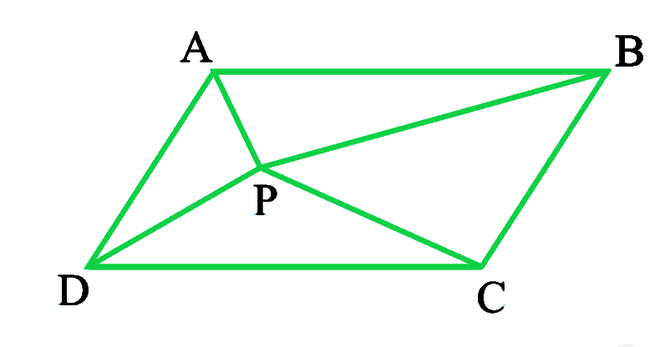
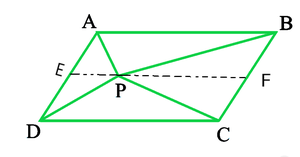
问题4:在图中,P是平行四边形ABCD内部的一个点。显示
(i)ar(APB)+ ar(PCD)= 1/2 ar(ABCD)
(ii)ar(APD)+ ar(PBC)= ar(APB)+ ar(PCD)
[提示:通过P,画一条与AB平行的线。]
解决方案:
Given: P is a point in the interior of the parallelogram ABCD
To prove: Area(APB) + Area(PCD) = ½ Area(ABCD)
Construction:
Through P, draw a line EF parallel to AB
Proof:
(i) In a parallelogram,
AB || EF (by construction) — (i)
∴AD || BC ⇒ AE || BF — (ii)
From equations (i) and (ii),
ABFE is a parallelogram.
Now,
ΔAPB and parallelogram ABFE are lying on the same base AB and ΔAPB lie in-between the same parallel lines AB and EF.
∴ ar(ΔAPB) = ½ ar(ABFE) — (iii)
also,
ΔPCD and parallelogram CDEF are lying on the same base CD and ΔPCD lie in-between the same parallel lines CD and EF.
∴ ar(ΔPCD) = ½ ar(CDEF) — (iv)
Adding equations (iii) and (iv) we get,
ar(ΔAPB) + ar(ΔPCD) = ½ [ar(ABFE)+ar(CDEF)]
⇒ ar(APB)+ ar(PCD) = ½ ar(ABCD)
Hence Proved
(ii) Construction:
Through P, draw a line GH parallel to AB
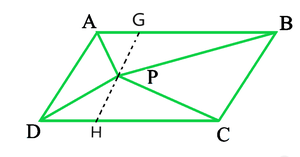
In the parallelogram,
AD || GH (by construction) — (i)
∴AB || CD ⇒ AG || DH — (ii)
From equations (i) and (ii) we get,
AGDH is a parallelogram.
Now,
ΔAPD and parallelogram AGHD are lying on the same base AD and ΔAPD lie in-between the same parallel lines AD and GH.
∴ar(ΔAPD) = ½ ar(AGHD) — (iii)
also,
ΔPBC and parallelogram BCHG are lying on the same base BC and ΔPBC lie in-between the same parallel lines BC and GH.
∴ar(ΔPBC) = ½ ar(BCHG) — (iv)
Adding equations (iii) and (iv) we get,
ar(ΔAPD) + ar(ΔPBC) = ½ {ar(AGHD) + ar(BCHG)}
⇒ ar(APD) + ar(PBC) = ar(APB) + ar(PCD)
Hence Proved
问题5:在图中,PQRS和ABRS是平行四边形,X是BR侧的任意点。显示:
(i)ar(PQRS)= ar(ABRS)
(ii)ar(AXS)=½ar(PQRS)
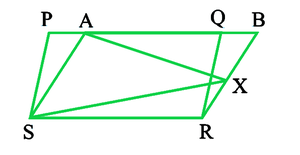
解决方案:
Given: PQRS and ABRS are parallelograms and X is any point on side BR
To Prove: (i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = ½ ar (PQRS)
Proof:
(i) In ΔPSA and ΔQRB,
∠ SPA = ∠ RQB — (i) (Corrosponding Angles from PS || QR and traversal PB
∠ PAS = ∠ QBR — (ii) (Corrosponding Angles from AS || BR and traversal PB
∠ PSA = ∠ QRB — (iii) (Angle Sum Property of tringle)
Also, PS = QR — (iv) (Opposite sides of Parallelogram PQRS)
In view of (i), (iii) and (iv),
ΔPSA ≅ ΔQRB — (v) (By ASA Rule)
∴ Area(ΔPSA) = Area(ΔQRB) — (vi)
∴ Congruent figures have Equal Area
Now, ar(PQRS) = Area(ΔPSA) + Area(AQRS)
= Area(ΔQRB) + Area(AQRS) —–|| Using (vi)
= ar(ABRS)
∴ar (PQRS) = ar (ABRS)
Hence Proved
(ii) ΔAXS and Parallelogram ABRS are on the Same base As and between the Same parallels AS and BR
∴ Area(ΔAXS) = ½ Area(Parallelogram ABRS)
= ½ {Area(AQRS) + Area(ΔQRB)}
= ½ Area(Parallelogram PQRS)
Hence Proved
问题6:一个农民有一块平行四边形PQRS形式的田地。她在RS上取得了任意点A,并将其与点P和Q相连接。这些字段分为多少部分?这些零件的形状是什么?农民想在田地的相等部分分别播种小麦和豆类。她应该怎么做?
解决方案:
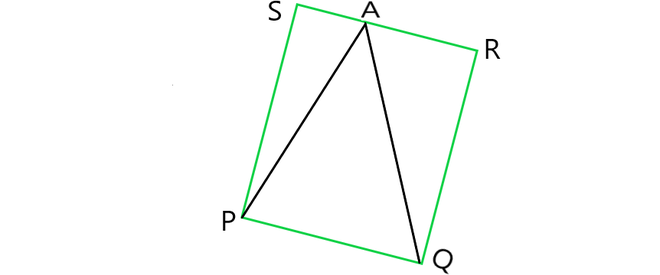
The field is divided into three parts each in triangular shape.
Let, ΔPSA, ΔPAQ and ΔQAR be the triangles.
Area of (ΔPSA + ΔPAQ + ΔQAR) = Area of PQRS — (i)
Area of ΔPAQ = ½ area of PQRS — (ii)
Here, the triangle and parallelogram are on the same base and in-between the same parallel lines.
From (i) and (ii) we get,
Area of ΔPSA + Area of ΔQAR = ½ area of PQRS — (iii)
From (ii) and (iii), we can conclude that,
The farmer must sow wheat or pulses in ΔPAQ or either in both ΔPSA and ΔQAR.