在几何中,等腰三角形是具有相等边长的两个边的三角形。有时将其指定为恰好具有相等长度的两个边,有时将其指定为至少具有相等长度的两个边,因此,后者的形式在特殊情况下包括等边三角形。等腰三角形的例子包括等腰直角三角形,金色三角形,双锥面和某些加泰罗尼亚实体。
Theorem Statement: Angle opposite to equal sides of an isosceles triangle are equal.
证明:
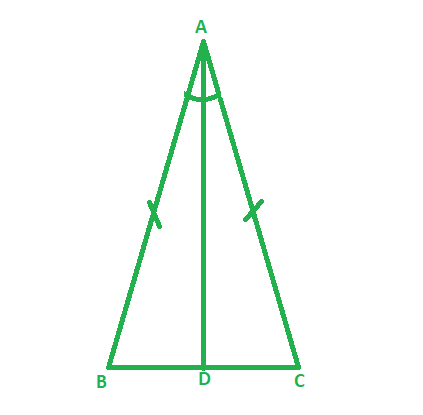
Given, an Isosceles triangle ABC, where the length of side AB equals the length of side AC.
Therefore, AB = AC
Construction:
Let us draw the bisector of ∠A
Let D be the point of intersection of this bisector of ∠A and BC.
Therefore ,by construction ∠BAD = ∠CAD.
In ∆BAD and ∆DAC,
AB = AC (Given)
∠BAD = ∠CAD (By construction)
AD = AD (Common side in both triangle)
So, ∆BAD ≅ ∆CAD (By SAS rule)
So, ∠ABD = ∠ACD, since they are corresponding angles of congruent triangles.
So, ∠B = ∠C
Hence, Proved that an angle opposite to equal sides of an isosceles triangle is equal.
Note:
The converse of this theorem is also true. The sides opposite to equal angles of a triangle are also equal.
基于定理的样本问题
问题1:E和F分别是∆ABC的等边AB和AC的中点(请参见给定图)。证明BF = CE。
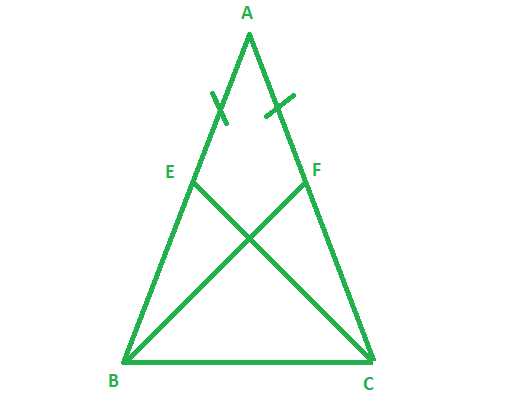
解决方案:
Given:
Length of side AB = AC
To show: BF = CE
In ∆ABF and ∆ACE,
AB = AC (Given)
∠A = ∠A (Common)
AF = AE (Halves of equal sides)
So, ∆ABF ≅ ∆ACE (SAS rule)
Since, If two triangles are congruent, their corresponding sides are equal.
Therefore, BF = CE ( by CPCT)
问题2:给定∆ABC的周长为13厘米,∠ABC=∠ACB,且BC边的长度等于3 cm。求出AB和AC边的长度。
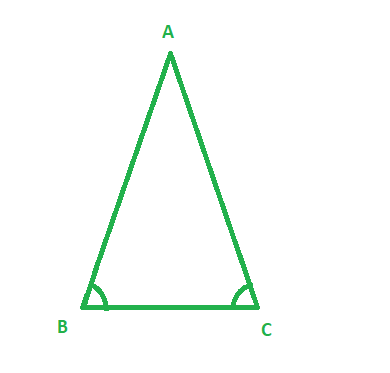
解决方案:
Given:
BC = 3cm, Perimeter of ∆ABC = 13cm
∠ABC = ∠ACB
Since ∠ABC = ∠ACB , therefore by applying theorem, the sides opposite to equal angles of a triangle are also equal.
So, length of side AB = AC.
Let the side of AB be x.
Therefore, Perimeter = AB + BC + AC
13 = x + 3 + x ( Since, AB = AC )
13 = 2x + 3
13 – 3 = 2x
10/2 = x
Therefore x = 5
So, the length of side AB and AC is 5 cm.