第 12 类 RD Sharma 解决方案 - 第 21 章有界区域 - 练习 21.1 |设置 3

问题 21. 画出曲线的粗略草图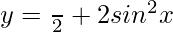$y=\frac{π}{2}+2sin^2x$并找到 x 轴、曲线和纵坐标之间的面积 x = 0, x = π

解决方案：

Here, we have to find the bounded by 

$y=\frac{\pi}{2}+2sin^2x$

x-axis, x = 0 and x = π

Here is the table for values of $y=\frac{\pi}{2}+2sin^2x$

x	0	$\frac{\pi}{6}$	$\frac{\pi}{4}$                     $\frac{\pi}{3}$	$\frac{\pi}{2}$	$\frac{2\pi}{3}$                $\frac{3\pi}{4}$	$\frac{5\pi}{6}$	π
$\frac{\pi}{2}+2\ sin^2x$	1.57	2.07	2.57                  3.07	3.57	3.07            2.57	2.07	1.57

Here is the rough sketch,

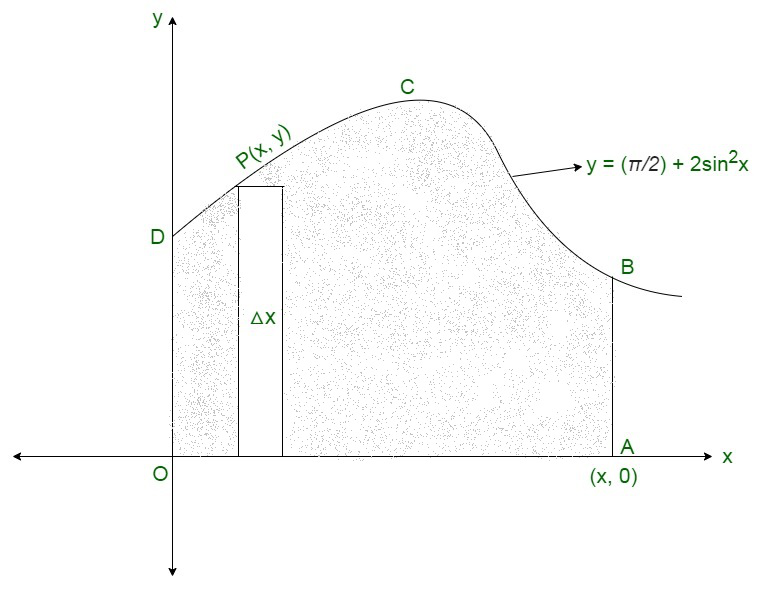
Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = π,

Thus,

Required area = Region ABCDO

$\displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2}+π-\frac{sin\ 2x}{2}\right)-(0)\right]\\ =\frac{π^2}{2}+π$

Required area = $\frac{π}{2}(π+2)$ square units

问题 22. 画出曲线的粗略草图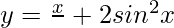$y=\frac{x}{π}+2sin^2x$并找到 x 轴、曲线和纵坐标 x = 0, x = π 之间的面积。

解决方案：

Here, we have the area between y-axis,

x = 0,

x = π

and

$y=\frac{x}{π}+2\ sin^2x\ \ \ \ \ ......(1)$

Thus, the table for equation (1) is

x	0      $\frac{π}{6}$	$\frac{π}{4}$	$\frac{π}{3}$	$\frac{π}{2}\ \ \ \ \frac{2π}{3}\ \ \ \ \ \frac{3π}{4}\ \ \ \ \ \frac{5π}{6}$	π
y	0         0.66	1.25	1.88	2.5  1.88   1.25   0.66	0

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = π,

Thus,

Required area = Region ABOA

$\displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2x}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2x}+π-0\right)-(0)\right]\\$

Required area = $\frac{3\pi}{2}$ square units

问题 23. 求曲线 y = cos x 在 x = 0 和 x = 2 π之间的面积

解决方案：

Here from the figure we can see that

The required area = area of the region OABO + area of the region BCDB + area of the region DEFD

Therefore,

The required area = $\displaystyle \int_0^{\frac{\pi}{2}}cos\ x\ dx+\left|\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}cos\ x\ dx\right|+\int_{\frac{3\pi}{2}}^{2\pi}cos\ x\ dx\\ =[sin\ x]_0^{\frac{\pi}{2}}+\left|[sin\ x]^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\right|+[sin\ x]^{2\pi}_{\frac{3\pi}{2}}\\ =\left[sin\frac{\pi}{2}-sin0\right]+\left|sin\frac{3\pi}{2}-sin\frac{\pi}{2}\right|+\left[sin\ 2x-sin\frac{3\pi}{2}\right]\\ =1+2+1\\ =4\ sq.\ units$

问题 24. 证明曲线 y = sin x 和 y = sin 2x 在 x = 0 和 x = 之间的面积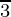$\frac{π}{3}$比例为 2:3。

解决方案：

We have to find the area under the curve

y = sin x    ……..(1)

and

y = sin 2x     …………(2)

Between x = 0 and x = $\frac{\pi}{3}$

x y = sin x	$0\ \ \ \ \ \ \frac{\pi}{6}\ \ \ \ \ \ \frac{\pi}{4}\ \ \ \ \ \ \ \frac{\pi}{3}\\ 0\ \ \ \ \ 0.5\ \ \ \ 0.7\ \ \ \ 0.8$	$\frac{\pi}{2}\\ 1$
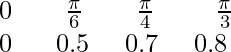
y = sin 2x	0      0.8       1       0.8	0

Here is the rough sketch 

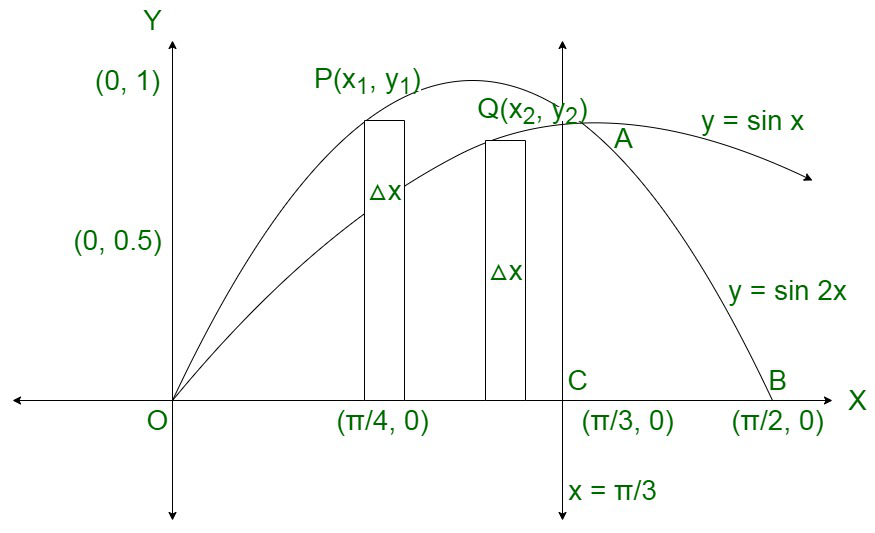
Area under curve y = sin 2x

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y1

Area of rectangle = y1△x

The approx rectangles slide from x = 0 to x = $\frac{\pi}{3}$,

Thus,

Required area = Region OPACO

$\displaystyle A_1=\int_0^{\frac{\pi}{3}}y_1\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ 2x\ dx\\ =\left[\frac{-cos\ 2x}{2}\right]_0^{\frac{\pi}{3}}\\ =-\left[-\frac{1}{4}-\frac{1}{2}\right]\\ A_1=\frac{3}{4}\ sq.\ units$

We slice it into approximation rectangle of 

Width = △x

Length = y2

Area of rectangle = y2△x

The approx rectangles slide from x = 0 to x = $\frac{\pi}{3}$,

Thus,

Required area = Region OQACO

$\displaystyle =\int_0^{\frac{\pi}{3}}y_2\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ x\ dx\\ =\left[{-cos\ x}\right]_0^{\frac{\pi}{3}}\\ =-\left[\frac{1}{2}-1\right]\\ A_2=\frac{1}{2}\ sq.\ units$

Thus,

$A_2:A_1=\frac{1}{2}:\frac{3}{4}\\ A_2:A_1=2:3$

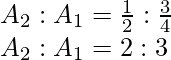
问题 25. 比较曲线 y = cos ² x 和 y = sin ² x 在 x = 0 和 x = π之间的面积

解决方案：

Here to compare area under curves

y = cos²x

and

y = sin²x

Between x = 0 and x = π

This is the table for y = cos²x and y = sin²x

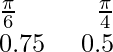
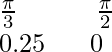
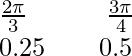
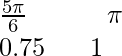
x y = cos2x	0 1	$\frac{\pi}{6}\ \ \ \ \ \ \ \ \ \frac{\pi}{4}\\ 0.75\ \ \ \ 0.5$	$\frac{\pi}{3}\ \ \ \ \ \ \ \ \ \frac{\pi}{2}\\ 0.25\ \ \ \ \ 0$	$\frac{2\pi}{3}\ \ \ \ \ \ \ \ \ \frac{3\pi}{4}\\ 0.25\ \ \ \ \ \ 0.5$	$\frac{5\pi}{6}\ \ \ \ \ \ \ \ \ \pi\\ 0.75\ \ \ \ \ 1$
y = sin2x	0	0.25          0.5	0.75      1	0.75     0.5	0.25       0

Area of region enclosed by

y = cos²x and axis

A₁ = Region OABO + Region BCDB

= 2(Region BCDB)

$\displaystyle =2\int_{\frac{\pi}{2}}^\pi cos^2x\ dx\\ =2\int_{\frac{\pi}{2}}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\left[x-\frac{sin\ 2x}{2}\right]^\pi_{\frac{\pi}{2}}\\ =\left[(x-0)-\left(\frac{\pi}{2}-0\right)\right]\\ =\pi-\frac{\pi}{2}\\ A_1=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(1)$ 

Area of region enclosed by y = sin²x and axis

A₂ = Region OEDO

$\displaystyle =\int_{0}^\pi sin^2x\ dx\\ =\int_{0}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\frac{1}{2}\left[x-\frac{sin\ 2x}{2}\right]^\pi_{0}\\ =\frac{1}{2}[(x-0)-(0)]\\ A_2=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(2)$

From equation (1) and (2),

A₁ = A₂

Thus,

Area enclosed by y = cos²x = Area enclosed by y = sin²x.

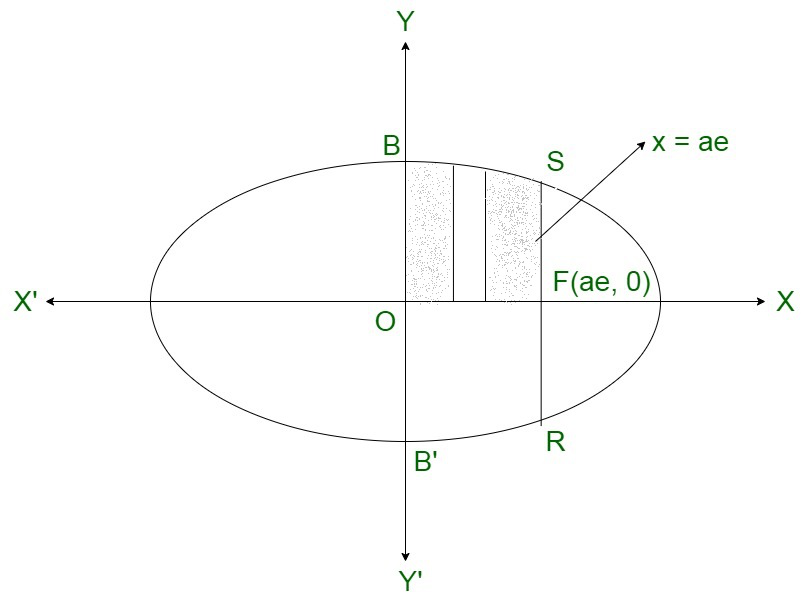
问题 26. 找出以椭圆为界的区域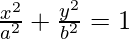$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$和纵坐标 x = 0 和 x = ae，其中 b ² = a ² (1 – e ² ) 和 e < 1。

解决方案：

Thus, the required area in the figure below of the region BOB’RFSB is enclosed by the ellipse and the lines x = 0 and x = ae

Here is the area of the region BOB’RFSB

$\displaystyle =2\int_0^{ae}y\ dx\\ =2\frac{b}{a}\int_0^{ae}\sqrt{a^2-x^2}\ dx\\ =\frac{2b}{a}\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^{ae}\\ =\frac{2b}{2a}\left[ae\sqrt{a^2-a^2e^2}+a^2sin^{-1}e\right]\\ =ab\left[e\sqrt{1-e^2}+sin^{-1}e\right]$

问题 27. 求圆 x ^{2 +} y ² = 由直线 x = 截断的小段的面积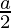$\frac{a}{2}$ .

解决方案：

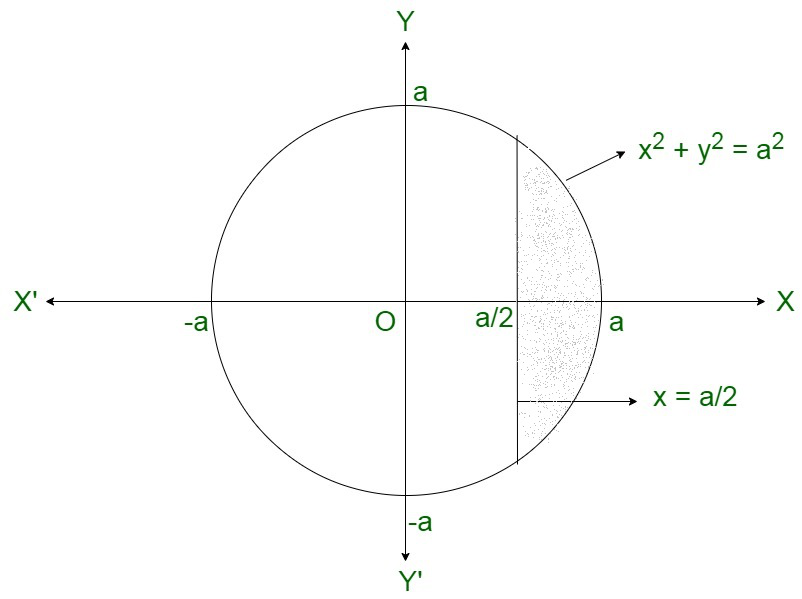
Area of the mirror segment of the circle

$\displaystyle =2\int_{\frac{a}{2}}^a\sqrt{a^2-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{2}\right]_{\frac{a}{2}^a}\\ =2\left[\frac{a}{2}(0)+\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =2\left[\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =\frac{a^2}{12}[4\pi-3\sqrt3]\ sq.\ units$

问题 28. 求曲线 x = at, y = 2at 在对应 t = 1 和 t = 2 的纵坐标之间的区域面积。

解决方案：

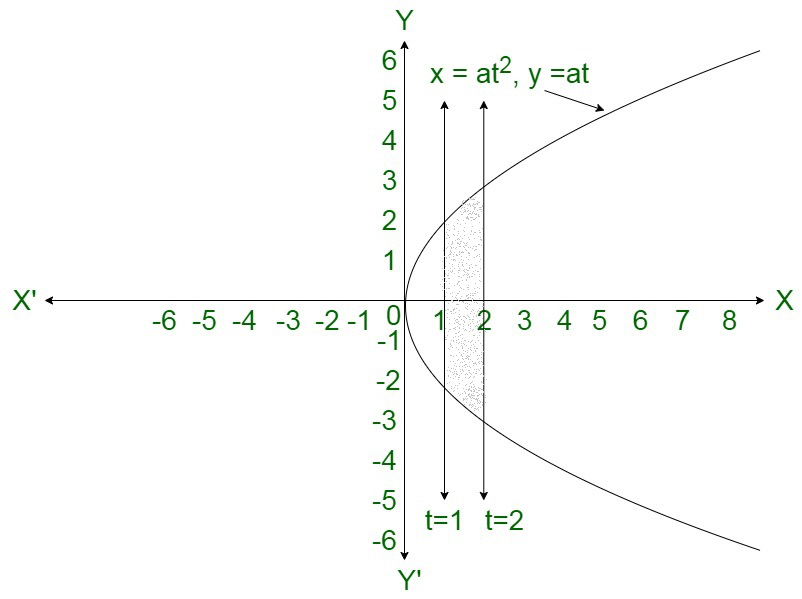
Area of the bounded region

$\displaystyle =2\int_1^2y\ \frac{dx}{dt}\ dt\\ =2\int_1^2(2at)(2at)\ dt\\ =8a^2\int_1^2t^2\ dt\\ =8a^2\left[\frac{t^3}{3}\right]_1^2\\ =8a^2\left[\frac{8}{3}-\frac{1}{3}\right]\\ =\frac{56a^2}{3}\ sq.\ units$

问题 29. 求曲线 x = 3 cos t, y = 2 sin t 所包围的面积。

解决方案：

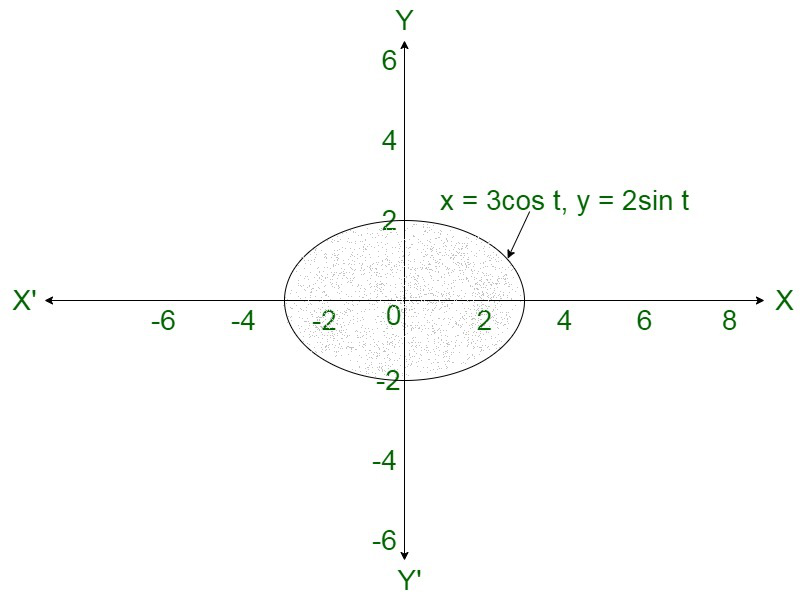
Area of the bounded region

$\displaystyle =4\int_0^{\frac{\pi}{2}}2sin\ t\ dt\\ =-8[cos\ t]_0^{\frac{\pi}{2}}$

= -8 [0 – 1]

= 8 square units