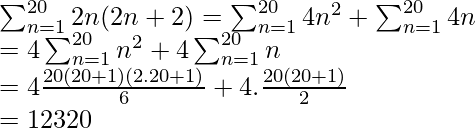11类RD Sharma解决方案–第21章一些特殊系列-练习21.1

求出以下序列与n个项之和(问题1-5)

问题1. 1 ³ + 3 ³ + 5 ³ + 7 ³ +……

解决方案：

Let us assume T_n to be the nth term of the given series.

Now, we have:

T_n = [1 + (n – 1)2]³

= (2n – 1)³

= (2n)³ – 3 (2n)². 1 + 3.1².2n – 1³  [Since, (a – b)³ = a³ – 3a²b + 3ab² – b]

= 8n³ – 12n² + 6n – 1

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n [2k-1]^3 \\ = \sum_{k=1}^n [8k^3 - 1 - 6k(2k-1)] \\ = \sum_{k=1}^n [8k^3 - 1 - 12k^2 + 6k] \\ = 8 \sum_{k=1}^n k^3 - \sum_{k=1}^n 1 - 12 \sum_{k=1}^n k^2 + 6 \sum_{k=1}^n k \\ = \frac{8n^2(n+1)^2}{4} - n - \frac{12n(n+1)(2n+1)}{6} + \frac{6n(n+1)}{2}$

Simplifying the equation we get

= 2n² (n + 1)² – n – 2n (n + 1) (2n + 1) + 3n (n + 1)

= n (n + 1) [2n (n + 1) – 2 (2n + 1) + 3] – n

= n (n + 1) [2n² – 2n + 1] – n

= n [2n³ – 2n² + n + 2n² – 2n + 1 – 1]

= n [2n³ – n]

= n² [2n² – 1]

Therefore, 

The sum of the series is n² [2n² – 1].

问题2。2 ³ + 4 ³ + 6 ³ + 8 ³ +………

解决方案：

Let us assume T_n to be the nth term of the given series.

Now, we have:

T_n = (2n)³

= 8n³

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n 8k^3 \\ = 8 \sum_{k=1}^n k^3 \\ = 8[\frac{n(n+1)}{2}]^2 \\ = 8 * \frac{n^2(n+1)^2}{4} \\ = 2n^2(n+1)^2 \\ = 2{n(n+1)}^2$

Therefore, 

The sum of the given series is 2{n (n + 1)}²

问题3. 1.2.5 + 2.3.6 + 3.4.7 +……

解决方案：

Let us assume T_n to be the nth term of the given series.

Now, we have:

T_n = n (n + 1) (n + 4)

= n (n² + 5n + 4)

= n³ + 5n² + 4n

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_k \\ \sum_{k=1}^n k^3 + \sum_{k=1}^n 5k^2 + \sum_{k=1}^n4k \\ = \sum_{k=1}^nk^3 + 5 \sum_{k=1}^nk^2 + 4 \sum_{k=1}^n \\ = \frac{n^2(n+1)^2}{4} + \frac{5n(n+1)(2n+1)}{6} + \frac{4n(n+1)}{2} \\ = \frac{n^2(n+1)^2}{4} + \frac{5n(n+1)(2n+1)}{6} + 2n(n+1) \\ = \frac{n(n+1)}{2} (\frac{n(n+1)}{2} + \frac{5(2n+1)}{3} + 4 ) \\ = \frac{n(n+1)}{2} (\frac{n^2 + n}{2} + \frac{10n+5}{3} + 4 ) \\ = \frac{n(n+1)}{2} (\frac{3n^2 + 3n + 20n + 10 + 24}{6}) \\ = \frac{n}{12} (n+1)(3n^2+23n+34) \\ = \frac{n(n+1)}{2}(\frac{3n^2+3n+20n+10+24}{6}) \\ = \frac{n}{12} (n+1) (3n^2 + 23n + 34)$

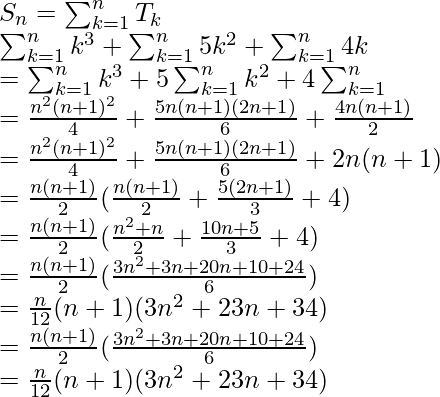
Therefore, 

The sum of the given series is $\frac{n}{12}(n+1)(3n^2 + 23n + 34)$

问题4. 1.2.4 + 2.3.7 + 3.4.10 +…。

解决方案：

Let us assume T_n to be the nth term of the given series.

Now, we have:

T_n = n (n + 1) (3n + 1)

= n (3n² + 4n + 1)

= 3n³ + 4n² + n

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n 3k^3 + \sum_{k=1}^n 4k^2 + \sum_{k=1}^n k \\ = 3\sum_{k=1}^n k^3 + 4\sum_{k=1}^n k^2 + \sum_{k=1}^n k \\ = \frac{3n^2(n+1)^2}{4} + \frac{4n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} \\ = \frac{3n^2(n+1)^2}{4} + \frac{2n(n+1)(2n+1)}{3} + \frac{n(n+1)}{2} \\ = \frac{n(n+1)}{2} (\frac{3n(n+1)}{2} + \frac{4(2n+1)}{3} + 1 ) \\ = \frac{n(n+1)}{2} (\frac{3n^2+3n}{2} + \frac{8n+4}{3} + 1) \\ = \frac{n(n+1)}{2} (\frac{9n^2+9n+16n+8+6}{6}) \\ = \frac{n}{12}(n+1)(9n^2+25n+14)$

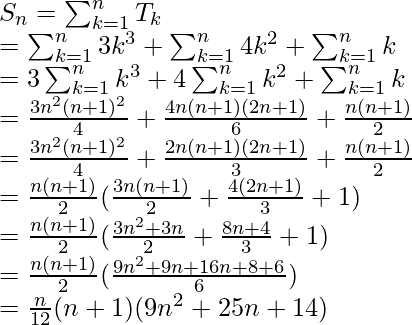
Therefore, 

The sum of the given series is $\frac{n}{12}(n+1)(9n^2 + 25n + 14)$

问题5. 1 +(1 + 2)+(1 + 2 + 3)+(1 + 2 + 3 + 4)+…

解决方案：

Let us assume T_n to be the nth term of the given series.

Now, we have:

T_n = n(n + 1)/2

= (n² + n)/2

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n (\frac{k^2+k}{2}) \\ = 1/2 \sum_{k=1}^n (k^2+k) \\ = 1/2 [\frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} ] \\ = \frac{n(n+1)}{4}(\frac{2n+1}{3} + 1) \\ = \frac{n(n+1)}{4} (\frac{2n+4}{3}) \\ = \frac{n(n+1)(2n+4)}{12} \\ = \frac{n(n+1)(n+2)}{6}$

Therefore, 
The sum of the series is [n(n + 1)(n + 2)]/6

问题6.找到1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 +…最多n个项的和。

解决方案：

Let us assume T_n to be the nth term of the given series.
T_n = (nth term of 1, 2, 3..) x (nth term of 2, 3, 4…)

= [1 + (n + 1) x 1].[2 + (n + 1) x 1]

= [1 + n – 1].[2 + n – 1]

= n(n + 1)

= n² + n 

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (n^2 + n) \\ = \frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} \\ = \frac{n(n+1)(2n+1)+3n(n+1)}{6} \\ = \frac{n(n+1)[2n+1+3]}{6} \\ = \frac{n(n+1)[2n+4]}{6} \\ = \frac{n(n+1) x 2 (n+2)}{6} \\ = \frac{n}{6} (n+1)(n+2)$

问题7.找到3 n × 1 ² + 5 × 2 ² + 7 × 3 ² +…的n个项之和。

解决方案：

Let us assume T_n to be the nth term of the given series.

T_n = (nth term of 3, 5, 7..) x (nth term of 1², 2², 3²…)

= [3 + (n – 1) x 2].[n²]

= [2n + 1]. [n²]

= 2n³ + n²

T_n = 2n³ + n²

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (2n^3 + n^2) \\ = \sum_{k=1}^n 2n^3 + \sum_{k=1}^n n^2 \\ = 2 \sum_{k=1}^n n^3 + \sum_{k=1}^nn^2 \\ = 2[\frac{n(n+1)}{2}]^2 + [\frac{n(n+1)(2n+1)}{6}] \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1)}{6} \\ = [\frac{n(n+1)}{2}]^2 + \frac{n(n+1)(2n+1)}{6} \\ = \frac{n(n+1)}{6}[3n(n+1)+(2n+1)] \\ = \frac{n(n+1)}{6}[3n^2+3n+2n+1] \\ \frac{n}{6}(n+1)(3n^2+5n+1)$

Therefore, 

The sum of the series = $\frac{n}{6}(n+1)(3n^2+5n+1)$

问题8(i)。求出2n ³ + 3n ² – 1至n项的和。

解决方案：

T_n = 2n³ + 3n² – 1 

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^{n}T_k \\ = 2 \sum_{k=1}^{n} 2k^3+ \sum_{k=1}^{n}3k^2 - \sum_{k=1}^{n} 1 \\ = 2[\frac{n(n+1)}{2}]^2 + 3[\frac{n(n+1)(2n+1)}{6}] -n \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1) - n }{2} \\ = \frac{[n(n+1]^2+n(n+1)(2n+1)-n}{2} \\ = \frac{n}{2}[n(n+1)^2 + (n+1)(2n+1) - 2] \\ = \frac{n}{2} [n^3+n+2n^2+2n^2+3n-1] \\ = \frac{n}{2} [n^3+4n^2+4n-1]$

Sum of n terms = $\frac{n}{2} [n^3+4n^2+4n-1]$

问题8(ii)。求出n ³ – 3 ⁿ至n项的和。

解决方案：

T_n = n³ – 3ⁿ

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3-3^k) \\ = \sum_{k=1}^{n} k^3 - \sum_{k=1}^{n} 3^k \\ = [\frac{n(n+1)}{2}]^2-(3^1+3^2+...+3^n) \\ = \frac{n^2(n+1)^2}{4}-3\frac{3^n-1}{3-1} \\ = \frac{n^2(n+1)^2}{4}-\frac{3}{2}(3^n-1)$

问题8(iii)。找出n(n + 1)(n + 4)到n个项的和。

解决方案：

T_n = n(n + 1)(n + 4)

Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3+5k^2+4k) \\ = \sum_{k=1}^{n} k^3 + \sum_{k=1}^{n} 5k^2 + \sum_{k=1}^{n} 4k \\ = \sum_{k=1}^{n} k^3 + 5 \sum_{k=1}^{n} k^2 + 4 \sum_{k=1}^{n}k \\ = [\frac{n(n+1)}{2}]^2 + 5[\frac{n(n+10(2n+1)}{6}]+\frac{4n(n+1)}{2} \\ = \frac{1}{4}[n(n+1)]^2 + \frac{5n(n+1)(2n+1}{6}+2n(n+1) \\ = \frac{3[n(n+1)]^2+10n(n+1)(2n+1)+24n(n+1)}{12} \\ = \frac{n(n+1)}{12}[3n(n+1)+10(2n+1)+24] \\ = \frac{n(n+1)}{12}[3n^2+23n+34]$

问题8(iv)。找出(2n – 1) ²到n项的和。

解决方案：

T_n = (2n – 1)² 

$(2n)^2 + 1 -2n \\ = 4n^2 + 1 - 4n \\ = 4n^2 - 4n + 1$

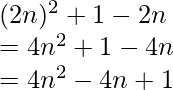
Also, let us assume S_n to be the sum of n terms of the given series.

$S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}4k +\sum_{k=1}^{n}1 \\ = \sum_{k=1}^{n}k^2 -4\sum_{k=1}^{n}k + \sum_{k=1}^{n}1 \\ = 4[\frac{n(n+1)(2n+1)}{6}]-4\frac{n(n+1)}{2}+n \\ = 2/3n(n+1)(2n+1)-2n(n+1)+n \\ = \frac{2}{3}n(n+1)(2n+1)-2n^2-2n+n \\ = \frac{2n}{3}(n+1)(2n+1) - n(2n+1) \\ = \frac{n}{3} (2n+1)[2(n+1)-3] \\ = \frac{n}{3}(2n+1)(2n+2-3) \\ = \frac{n}{3}(2n+1)(2n-1)$

问题9.找到系列2×4 + 4×6 + 6×8 +…的第20个项和20个项的总和。

解决方案：

Let us assume T_n to be the nth term of the given series.

$T_n = 2n(2n+2)$

The 20th term of the series is :

$T_{20} = 2 * 20(2*20+2) = 1680$

The infinite series is equivalent to, 

2 × 4 + 4 × 6 + 6 × 8 + …. = $\sum_{n=1} 2n(2n+2)$

Sum of the series until 20th term is equivalent to

$\sum_{n=1}^{20} 2n (2n+2) = \sum_{n=1}^{20}4n^2 + \sum_{n=1}^{20}4n \\ = 4 \sum_{n=1}^{20} n^2 + 4\sum_{n=1}^{20} n \\ = 4\frac{20(20+1)(2.20+1)}{6}+4. \frac{20(20+1)}{2} \\ = 12320$