下图中使用粗实线绘制了分段线性函数f(x)(该图按比例绘制)。
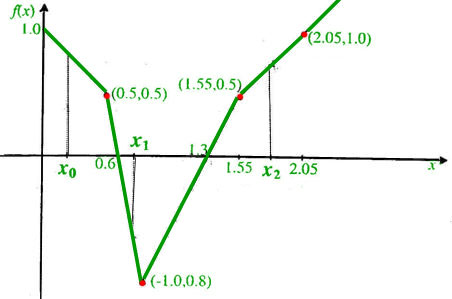
如果我们分别使用 x0、x1 和 x2 作为初始猜测,使用 Newton-Raphson 方法找到 f(x) = 0 的根,则得到的根将是
(A)分别为 1.3、0.6 和 0.6
(B)分别为 0.6、0.6 和 1.3
(C)分别为 1.3、1.3 和 0.6
(D)分别为 1.3、0.6 和 1.3答案: (D)
说明:首先,给定点的坐标有误。我已经用红色更正了。
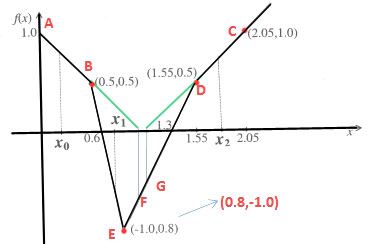
现在在 Newton-Raphson 方法中,我们从我们的猜测点绘制一条切线,我们的新猜测将是该切线切割 x 轴的点。现在我们一一选择初始猜测点:
x0 : Tangent at this point is line AB itself, and that would cut x-axis at
point (1.0,0.0) (found using equation of line AB). So our next guess
would be 1.0. Point on the curve corresponding to this new guess 1.0
is shown as F. Now tangent at point F is line DE, which cuts x-axis at
1.3, and at this point, value of function is zero, so we found the root
as 1.3.
x1 : Tangent at this point is line BE, which cuts x-axis at 0.6, also function
value is zero here, so we find root as 0.6.
x2 : Tangent at this point is line CD, which cuts x-axis at 1.05 (again found
by finding equation of line CD). Point on the curve corresponding to this
new guess 1.05 is shown as G. Now tangent at point G is line DE, which cuts
x-axis at 1.3, and at this point, value of function is zero, so we found
the root as 1.3. 来源:http://www.cse.iitd.ac.in/~mittal/gate/gate_math_2003.html 第 60 题
这个问题的测验