第 12 类 RD Sharma 解决方案 - 第 21 章有界区域 - 练习 21.1 |设置 1
问题 1. 使用积分,求直线 x = 2 和抛物线 y 2 = 8x 之间的区域面积
解决方案:
Here,
Given equations are:
x = 2 ……..(1)
y2 = 8x ……..(2)
Here,
Equation (1) represents a line parallel to y-axis and equation (2) represents a parabola with vertex at origin and x-axis,
Here is the rough sketch

We have to find the area of shaded region. We sliced it in vertical rectangle width of rectangle = △x,
Length = (y – 0) = y
Area of rectangle = y△x
This rectangle can move horizontal from x = 0 to x = 2
Required area = Shaded region OCBO
= 2 (Shaded region OABO)
= ![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2y\ dx\\ =2\times2\sqrt2\int_0^2\sqrt{x}\ dx\\ =4\sqrt2\left[\frac{2}{3}\times\sqrt{x}\right]_0^2\\ =4\sqrt2\left[\left(\frac{2}{3}\times2\sqrt2\right)-\left(\frac{2}{3}\right)\times0\sqrt0\right]\\ =4\sqrt2\left(\frac{4\sqrt2}{3}\right)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_1.jpg)
Required area = ![]() square units.
square units.
问题 2. 使用积分,找到以线 y – 1 = x、x 轴和纵坐标 x = -2 和 x = 3 为界的区域的面积。
解决方案:
The find area of region bounded by x-axis the ordinates x = -2 and x = 3
y – 1 = x ………….(1)
Equation (1) is a line that meets at axes at (0, 1) and (-1, 0)
Here, is the rough sketch

Required area is enclosed between the lines.
Required area = Region ABCA + Region ADEA
![Rendered by QuickLaTeX.com \displaystyle A=\int^3_{-1}y\ dx + \left|\int^{-1}_{-2}y\ dx\right|\\ =\int_{-1}^{3}(x+1)dx+\left|\int_{-2}^{-1}(x+1)dx\right|\\ =\left(\frac{x^2}{2}+x\right)_{-1}^3+\left|\left(\frac{x^2}{2}+x\right)_{-2}^{-1}\right|\\ =\left[\left(\frac{9}{3}+3\right)-\left(\frac{1}{2}-1\right)\right]+\left|\left(\frac{1}{2}-1(2-2)\right)\right|\\ =\left[\frac{15}{2}+\frac{1}{2}\right]+\left|-\frac{1}{2}\right|\\ =8+\frac{1}{2}\\ A=\frac{17}{2}\ square\ units.](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_4.jpg)
问题 3. 求抛物线 y 2 = 4ax 和直线 x = a 所围区域的面积
解决方案:
Here we have to find the area of the region that is bounded by
x = a ………(1)
and
y2 = 4a ………(2)
Equation (1) represents a line parallel to y-axis and equation (2) represent a parabola with vertex at origin and axis as x-axis.
Here, is the rough sketch

Here we have to find area between the region,
Thus, slice it in rectangles of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This assumed triangle can go from x = 0 to x = a.
Required area = Region OCBO
= 2 (Region OABO)
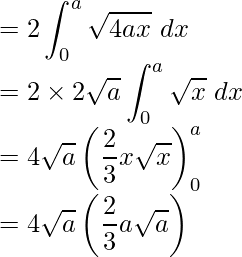
Required area = ![]() square units
square units
问题 4. 找到位于 x 轴上方和抛物线下方的区域 y = 4x – x 2 。
解决方案:
We have to find here the bounded area by x-axis and parabola
y = 4x – x2
x2 – 4x +4 = -y + 4
(x – 2)2 = -(y – 4) ……….(1)
Equation (1) represent a downward parabola with vertex (2, 4) and passing through (0, 0) and (0, 4).
Here is the rough sketch

Here the shaded region represents the required area.
We slice the region in approximation rectangles
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = a
Thus,
Required area = Region OABO
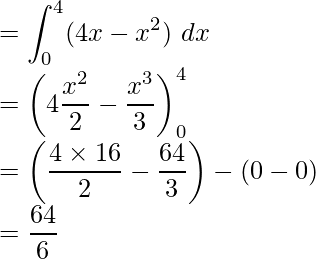
Required area = ![]() square units
square units
问题 5. 画一个粗略的草图,表示曲线 y 2 = 4x 和线 x = 3 之间的区域。另外,求这个区域的面积。
解决方案:
We have to find area bounded by
y2 = 4x ……..(1)
and
x = 3 ………..(2)
Equation (1) represents a parabola with vertex at origin and axis as x-axis and equation (2) represents a line parallel to y-axis
Here is the rough sketch

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
This approximation rectangle slide from x = 0 to x = 3
Required area = Region OCBO
= 2(Region OABO)
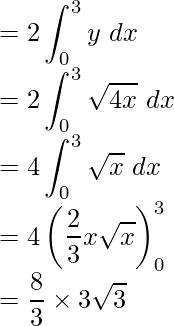
Required area = ![]() square units
square units
问题 6. 画出函数y = 4 – x 2 , 0 ≤ x ≤ 2 的图形,并确定曲线、x 轴和直线 x = 0 和 x = 2 所包围的面积。
解决方案:
Here, we will find the area enclosed by
y = 4 – x2
x2 = -(y – 4) ……….(1)
x = 0 ………(2)
x = 2 ……….(3)
Equation (1) represents a downward parabola with vertex at (0, 4) and passing through (2, 0), (-2, 0). Equation (2) represents y-axis and equation (3) represents a line parallel to y-axis.
Here’s a rough sketch

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
length = y – 0 = y
This approximation rectangle slide from x = 0 to x = 2
Required area = Region OABO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^2(4-x^2)\ dx\\ =\left(4x-\frac{x^3}{3}\right)_0^2\\ =\left[4(2)-\frac{(2)^3}{3}\right]-[0]\\ =\left[\frac{24-8}{3}\right]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_15.jpg)
Required area = ![]() square units.
square units.
问题 7. 画图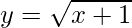 在 [0, 4] 中并确定由曲线、x 轴和线 x = 0 和 x = 4 包围的区域的面积。
在 [0, 4] 中并确定由曲线、x 轴和线 x = 0 和 x = 4 包围的区域的面积。
解决方案:
Here, we will find the area enclosed by x-axis and
![]()
y2 = x + 1 …….(1)
x = 0 ………(2)
x = 4 ………(3)
Equation (1) represents a parabola with vertex at (-1, 0) and passing through (0, 1) and (0, -1). Equation (2) represents y-axis and equation (3) represents a line parallel to y-axis passing through (4, 0).
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 4
Required area = Region OECDO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^4y\ dx\\ =\int_0^4\sqrt{x+1}\ dx\\ =\left(\frac{2}{3}(x+1)\sqrt{x+1}\right)_0^4\\ =\frac{2}{3}[((4+1)\sqrt{4+1})-((0+1)\sqrt{0+1})]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_20.jpg)
Required area = ![]() square units or
square units or ![]() square units.
square units.
问题 8. 求曲线下面积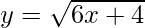 在 x 轴上方从 x = 0 到 x = 2。也画出曲线的草图。
在 x 轴上方从 x = 0 到 x = 2。也画出曲线的草图。
解决方案:
Here, we will find the area enclosed by x-axis
x = 0,
x = 2 ………(1)
y2 = 6x + 4 ……….(2)
Equation (1) represents y-axis and a line parallel to y-axis passing through (2, 0). Equation (2) represents a parabola with vertex at ![]() and passes through the points (0, 2) , ( 0, -2).
and passes through the points (0, 2) , ( 0, -2).
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 2,
Required area = Region OABCO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^2\sqrt{6x+4}\ dx\\ =\left(\frac{2}{3}\frac{(6x+4)\sqrt{6x+4}}{6}\right)_0^2\\ =\frac{1}{9}[((12+4)\sqrt{12+4})-((0+4)\sqrt{0+4})]\\ =\frac{1}{9}[16\sqrt{16}-4\sqrt{4}]\\ =\frac{1}{9}(64-8)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_26.jpg)
Required area = ![]() square units.
square units.
问题 9. 画出 y 2 + 1 = x, x ≤ 2 的草图。求曲线和直线 x = 2 所包围的面积。
解决方案:
Here, we will find the area enclosed by x-axis
y2 = x + 1 ……….(1)
and
x = 2 ……………(2)
Equation (1) is a parabola with vertex at (0, 1) and axis as x-axis.
Equation (2) represents a line parallel to y-axis passing through (2, 0)
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 2,
Required area = Region ABCA
= 2(Region AOCA)
![Rendered by QuickLaTeX.com \displaystyle =2\int_1^2y\ dx\\ =2\int_1^2\sqrt{x-1}\ dx\\ =2\left(\frac{2}{3}(x-1)\times\sqrt{x-1}^2\right)_1^2\\ =\frac{4}{3}[((2-1)\sqrt{2-1})-((1-1)\sqrt{1-1})]\\ =\frac{4}{3}(1-0)](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_29.jpg)
Required area = square units.
问题 10. 画出曲线图的粗略草图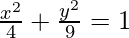 并评估曲线下方和 x 轴上方的区域面积
并评估曲线下方和 x 轴上方的区域面积
解决方案:

Here, we can observe that ellipse is symmetrical about x-axis.
Area bounded by ellipse = ![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2 y\ dx\\ = 2\int_0^23\sqrt{1-\frac{x^2}{4}}\ dx\\ =3\int\sqrt{4-x^2}\ dx\\ =3\left[\frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}sin^{-1}\frac{x}{2}\right]_0^2\\ =3[1(0)+2sin^{-1}-0-2sin^{-1}(0)]\\ =3[\pi]\\ =3\pi\ sq.\ units](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_21_Areas_of_Bounded_Regions_%E2%80%93_Exercise_21.1_%7C_Set_1_33.jpg)