第 11 类 RD Sharma 解——第 15 章线性不等式——练习 15.5

在二维平面上用图形表示下列不等式的解集：

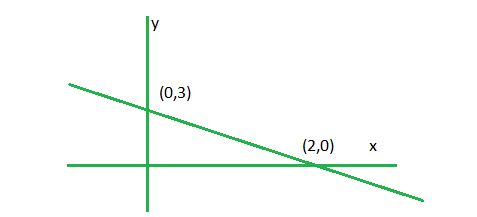
问题 1. x+2y-4 <=0

解决方案：

Step 1. Convert the given inequation into equation i.e. x+2y-4 =0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point.

Here we take (0,0) and (5,0).

Putting these points in x+2y-4 <= 0. (5,0) satisfies.

Shaded region is required answer.

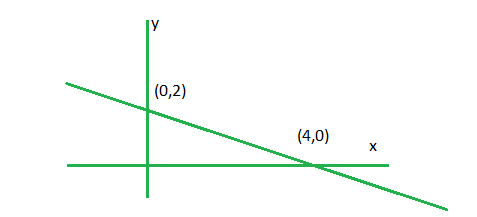
问题 2. x+2y >= 6

解决方案：

First writing the equation as x+2y-6 >=0.

Step 1. Convert the given inequation into equation i.e. x+2y-6 = 0.

Step 2. Plot the obtained equation on Cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point .

Here we take (0,0) and (3,0).

Putting these points in x+2y-6 >=0. (3,0) satisfies.

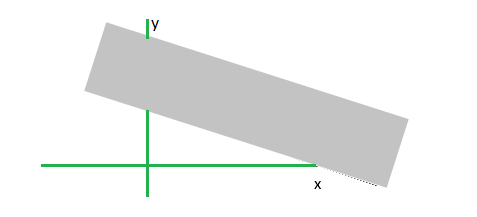
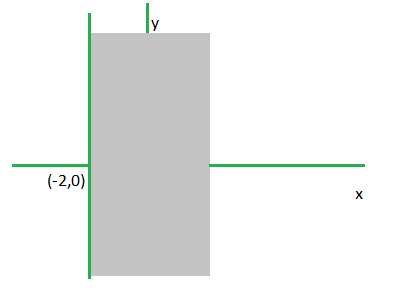
问题 3. x+2 >= 0。

解决方案：

Step 1. Convert the given inequation into equation i.e. x+2 = 0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Here inequality have one variable so x >= -2 ,hence shade the obtained region i.e.

问题 4. x-2y < 0。

解决方案：

Step 1. Convert the given inequation into equation i.e. x – 2y = 0

Step 2. Plot the obtained equation on cartesian plane.

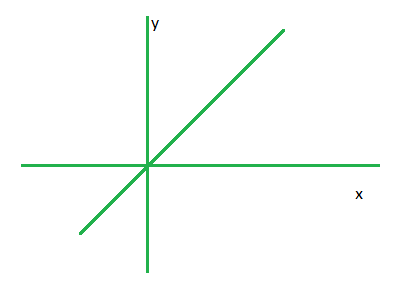
Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point

Here we take (0, 2) and (2, 0)

Putting these points in x-2y<0, (0, 2) satisfies

问题 5. -3x+2y <= 6

解决方案：

Firstly writing the inequation as -3x+2y-6 <= 0.

Step 1. Convert the given inequation into equation i.e. -3x+2y-6 = 0.

Step 2. Plot the obtained equation on cartesian plane.

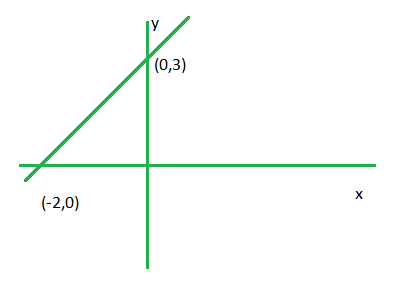
Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point.

Here we take (-1,0) and (-3,0).

Putting these points in -3x+2y-6 <= 0. (-1, 0) satisfies.

问题 6. x <= 8-4y。

解决方案：

At first write the inequality as x+4y-8 <= 0.

Step 1. Convert the given inequation into equation i.e. x+4y-8 = 0

Step 2. Plot the obtained equation on cartesian plane.

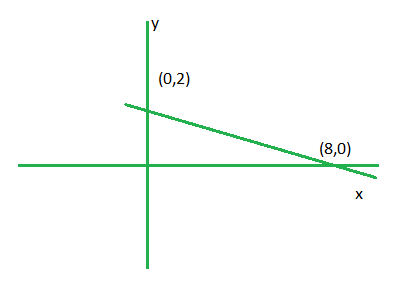
Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point

Here we take (0,0) and (9,0).

Putting these points in x+4y-8 <= 0. (0, 0) satisfies.

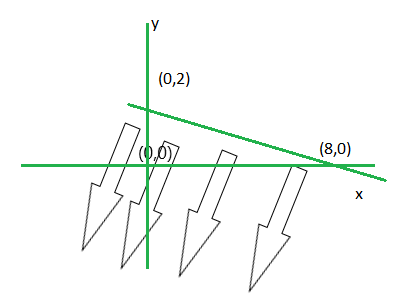
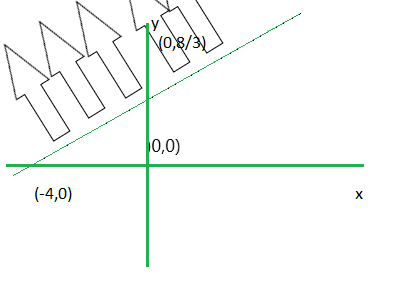
问题 7. 0 <= 2x-5y+10

解决方案：

First read the inequality as 2x-5y+10 >= 0.

Step 1. Convert the given inequation into equation i.e. 2x-5y+10 = 0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point.

Here we take (0,0) and (-6,0)

Putting these points in 2x-5y+10 >= 0. (0,0) satisfies.

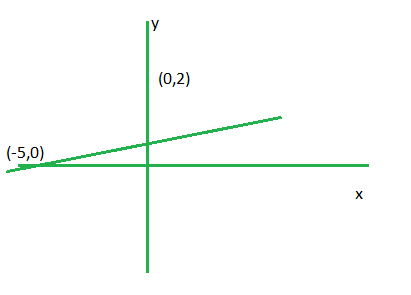
问题 8. 3y > 6-2x

解决方案：

First manipulate the inequation as 2x+3y-6 >0.

Step 1. Convert the given inequation into equation i.e.2x+3y-6= 0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point.

Here we take (0,0) and (4,0)

Putting these points in 2x+3y-6 >0 (4,0) satisfies.

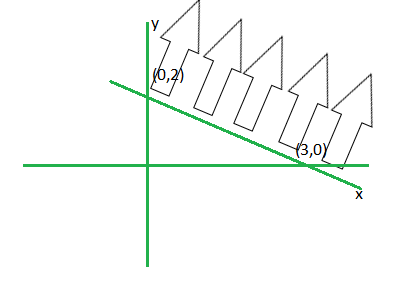
问题 9. y > 2x-8

解决方案：

First convert the inequation as -2x+y+8 >0.

Step 1. Convert the given inequation into equation i.e. -2x+y+8= 0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true, the required plot will be towards that point.

Here we take (0,0) and (5,0)

Putting these points in -2x+y+8 >0 (0,0) satisfies.

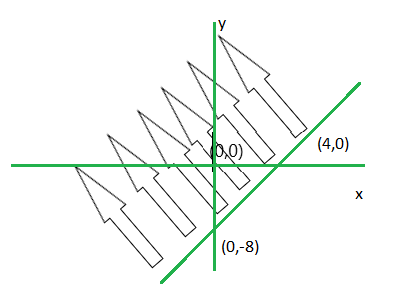
问题 10. 3x-2y <= x+y-8

解决方案：

First take all the variables in one side i.e. 2x-3y+8 <= 0.

Step 1. Convert the given inequation into equation i.e. 2x-3y+8 = 0

Step 2. Plot the obtained equation on cartesian plane.

Step 3. Take two points lying on each side of line and put it in inequality, the one which holds the inequality true ,the required plot will be towards that point.

Here we take (0,0) and (-5,0)

Putting these points in 2x-3y+8 <= 0. (-5,0) satisfies.