CBSE 11 级数学公式

GeeksforGeeks 为 11 年级数学学生带来了公式表，该表严格基于 NCERT 教学大纲，以简化学生为学校考试以及 JEE 和 NEET 等各种竞争性考试的准备和复习过程。本文不仅包括公式列表，还为学生提供章节摘要、要记住的要点、重要概念的简要说明和公式推导，以便更好地理解和保留章节。因此，这些分章的 CBSE 11 级数学公式旨在确保在任何考试中都做好充分的准备并取得良好的成绩。

第 1 章：集合

本章解释了集合的概念及其表示。讨论的主题是空集、等集、子集、有限集和无限集、幂集和全集。集合是对象的良好协作集合。由确定元素组成的集合是有限集。否则，它是一个无限集。以下是 Sets 中使用的重要术语和属性，如下所示：

• The union of two sets A and B are said to be contained elements that are either in set A and set B. The union of A and B is denoted as, A∪B.
• The intersection of two sets A and B are said to be contained elements that are common in both sets. The intersection of A and B is denoted as, A∩B. 
• The complement of a set A is the set of all elements given in the universal set U that are not contained in A. The complement of A is denoted as, A’.
  • For any two sets A and B, the following holds true:
    • (A∪B)′=A′∩B′
    • (A∩B)′=A′∪B′
• If the finite sets A and B are given such that, (A∩B)=ϕ, then:

n(A∪B)=n(A)+n(B)

• If (A∪B)=ϕ, then:

n(A∪B)=n(A)+n(B)−n(A∩B)

• Some other important formulas of Sets for any three sets A, B, and C are as follows:
  1. A – A = Ø
  2. B – A = B⋂ A’
  3. B – A = B – (A⋂B)
  4. (A – B) = A if A⋂B =  Ø
  5. (A – B) ⋂ C = (A⋂ C) – (B⋂C)
  6. A ΔB = (A-B) U (B- A)
  7. n(A∪B) = n(A) + n(B) – n(A⋂B)
  8. n(A∪B∪C)= n(A) +n(B) + n(C) – n(B⋂C) – n (A⋂ B)- n (A⋂C) + n(A⋂B⋂C)
  9. n(A – B) =  n(A∪B) – n(B)
  10. n(A – B) = n(A) – n(A⋂B)
  11. n(A’) = n(∪) – n(A)
  12. n(U) =  n(A) + n(B) + – n(A⋂B) + n((A∪B)’)
  13. n((A∪B)’) = n(U) +  n(A⋂B) – n(A) – n(B)

第 2 章：关系与功能

关系与函数一章使用有序和无序元素对的概念解释了集合论的高级概念。有序对是按一定顺序组合在一起的一对元素。集合 A 与集合 B 的关系 R 可以描述为笛卡尔积 A × B 的子集，该子集是通过描述其元素 x 的第一个和其元素 y 的第二个在有序对中给出的关系而获得的的 A × B。

The below-mentioned properties will surely assist students to solve various maths problems:

• Relations: A relation R is the subset of the cartesian product of A × B, where A and B are two non-empty elements. It is derived by stating the relationship between the first element and second element of the ordered pair of A × B.
• Inverse of Relation: A and B are any two non-empty sets. Let R be a relationship between two sets A and B. The inverse of relation R, indicated as R^-1, is a relationship that connects B and A and is defined by

R^-1 ={(b, a) : (a, b) ∈ R}

where, Domain of R = Range of R^-1 and Range of R = Domain of R^-1.

• Functions: A relation f from a set A to set B is said to be function, if every element of set A has one and only image in set B.
• A cartesian product A × B of two sets A and B is given by: A × B = { (a,b) : a ϵ A, b ϵ B}
  • If (a, b) = (x, y); then a = x and b = y
  • If n(A) = x and n(B) = y, then n(A × B) = xy and A × ϕϕ = ϕϕ
  • The cartesian product: A × B ≠ B × A.
• A function f from set A to set B considers a specific relation type where every element x in set A has one and only one image in set B. A function can be denoted as f : A → B, where f(x) = y.
• Algebra of functions: If the function f : X → R and g : X → R; we have:
  • (f + g)(x) = f(x) + g(x) ; x ϵ X
  • (f – g)(x) = f(x) – g(x)
  • (f . g)(x) = f(x).g(x)
  • (kf)(x) = k(f(x)) where k is a real number
  • {f/g}(x) = f(x)/g(x), g(x)≠0

第 3 章：三角函数

在数学中，三角函数是与直角三角形的角度相关的实函数，形成两个边长的一些有限比率。在下面找到与三角函数相关的第 11 课的重要数学公式。

• If in a circle of radius r, an arc of length l subtends an angle of θ radians, then l = r×θ.
  • Radian Measure = π/180 × Degree Measure
  • Degree Measure = 180/π × Radian Measure
• Trigonometric ratios:
  • sin θ = (Perpendicular (P)) / (Hypotenuse (H)).
  • cos θ = (Base (B)) / ( Hypotenuse (H)).
  • tan θ = (Perpendicular (P)) / (Base (B)).
  • cosec θ = (Hypotenuse (H)) / (Perpendicular (P)).
  • sec θ = (Hypotenuse (H)) / (Base (B)).
  • cot θ = (Base (B)) / (Perpendicular (P)).
• Reciprocal Trigonometric Ratios:
  • sin θ = 1 / (cosec θ)
  • cosec θ = 1 / (sin θ)
  • cos θ = 1 / (sec θ)
  • sec θ = 1 / (cos θ)
  • tan θ =  1 / (cot θ)
  • cot θ = 1 / (tan θ)
• Trigonometric Ratios of Complementary Angles:
  • sin (90° – θ) = cos θ
  • cos (90° – θ) = sin θ
  • tan (90° – θ) = cot θ
  • cot (90° – θ) = tan θ
  • sec (90° – θ) = cosec θ
  • cosec (90° – θ) = sec θ
• Periodic Trigonometric Ratios
  • sin(π/2-θ) = cos θ
  • cos(π/2-θ) = sin θ
  • sin(π-θ) = sin θ
  • cos(π-θ) = -cos θ
  • sin(π+θ)=-sin θ
  • cos(π+θ)=-cos θ
  • sin(2π-θ) = -sin θ
  • cos(2π-θ) = cos θ
• Trigonometric Identities
  • sin² θ + cos² θ = 1 ⇒ sin² θ = 1 – cos² θ ⇒ cos² θ = 1 – sin² θ
  • cosec² θ – cot² θ = 1 ⇒ cosec² θ = 1 + cot² θ ⇒ cot² θ = cosec² θ – 1
  • sec² θ – tan² θ = 1 ⇒ sec² θ = 1 + tan² θ ⇒ tan² θ = sec² θ – 1
• Product to Sum Formulas
  • sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
  • cos x cos y = 1/2[cos(x–y) + cos(x+y)]
  • sin x cos y = 1/2[sin(x+y) + sin(x−y)]
  • cos x sin y = 1/2[sin(x+y) – sin(x−y)]
• Sum to Product Formulas
  • sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2]
  • sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2]
  • cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2]
  • cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2]
• General Trigonometric Formulas:
  • sin (x+y) = sin x × cos y + cos x × sin y
  • cos(x+y)=cosx×cosy−sinx×siny
  • cos(x–y)=cosx×cosy+sinx×siny
    sin(x–y)=sinx×cosy−cosx×siny
  • If there are no angles x, y and (x ± y) is an odd multiple of (π / 2); then:
    • tan (x+y) = tan x + tan y / 1 − tan x tan y
    • tan (x−y) = tan x − tan y / 1 + tan x tan y
  • If there are no angles x, y and (x ± y) is an odd multiple of π; then:
    • cot (x+y) = cot x cot y−1 / cot y + cot x
    • cot (x−y) = cot x cot y+1 / cot y − cot x
• Formulas for twice of the angles:
  • sin2θ = 2sinθ cosθ = [2tan θ /(1+tan2θ)]
  • cos2θ = cos2θ–sin2θ = 1–2sin2θ = 2cos2θ–1= [(1-tan2θ)/(1+tan2θ)]
  • tan 2θ = (2 tan θ)/(1-tan2θ)
• Formulas for thrice of the angles:
  • sin 3θ = 3sin θ – 4sin 3θ
  • cos 3θ = 4cos 3θ – 3cos θ
  • tan 3θ = [3tan θ–tan 3θ]/[1−3tan 2θ]

第四章：数学归纳原理

顾名思义，本章解释了数学归纳原理的概念。讨论的主题是证明归纳的过程和激励应用程序将自然数作为实数的最小归纳子集的过程。数学思维的一个关键基础是演绎推理。与演绎相反，归纳推理依赖于处理不同的案例并通过观察发生率来发展猜想，直到我们观察到每一个案例。因此，用简单的语言，我们可以说“归纳”这个词意味着从特定案例或事实的概括。

Below mentioned is the list of some important terms and steps used in the chapter mentioned above:

• Statement: A sentence is called a statement if it is either true or false.
• Motivation: Motivation is tending to initiate an action. Here Basis step motivate us for mathematical induction.
• Principle of Mathematical Induction: The principle of mathematical induction is one such tool that can be used to prove a wide variety of mathematical statements. Each such statement is assumed as P(n) associated with positive integer n, for which the correctness for the case n = 1 is examined. Then assuming the truth of P(k) for some positive integer k, the truth of P (k+1) is established.
• Working Rule:
  • Step 1: Show that the given statement is true for n = 1.
  • Step 2: Assume that the statement is true for n = k.
  • Step 3: Using the assumption made in step 2, show that the statement is true for n = k  + 1. We have proved the statement is true for n = k. According to step 3, it is also true for k + 1 (i.e., 1 + 1 = 2). By repeating the above logic, it is true for every natural number.

第 5 章：复数和二次方程

因此，正如本章名称所暗示的那样，本章解释了复数和二次方程的概念及其性质。讨论的主题是复数的平方根、代数性质、argand 平面和极坐标表示、复数系统中的二次方程的解。与复数和二次方程相关的几个要点如下：

• Complex Numbers: A number that can be expressed in the form a + b is known as the complex number; where a and b are the real numbers and i is the imaginary part of the complex number.
• Imaginary Numbers: The square root of a negative real number is called an imaginary number, e.g. √-2, √-5 etc. The quantity √-1 is an imaginary unit and it is denoted by ‘i’ called iota.

i = √-1, i² = -1, i³ = -i, i⁴ = 1

• Equality of Complex Number: Two complex numbers z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ are equal, iff x₁ = x₂ and y₁ = y₂ i.e. Re(z₁) = Re(z₂) and Im(z₁) = Im(z₂)

Algebra of Complex Numbers

• Addition: Consider z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ are any two complex numbers, then their sum is defined as

z₁ + z₂ = (x₁ + iy₁) + (x₂ + iy₂) = (x₁ + x₂) + i (y₁ + y₂)

• Subtraction: Consider z₁ = (x₁ + iy₁) and z₂ = (x₂ + iy₂) are any two complex numbers, then their difference is defined as

z₁ – z₂ = (x₁ + iy₁) – (x₂ + iy₂) = (x₁ – x₂) + i(y₁ – y₂)

• Multiplication: Consider z₁ = (x₁ + iy₁) and z₂ = (x₂ + iy₂) be any two complex numbers, then their multiplication is defined as

z₁z₂ = (x₁ + iy₁) (x₂ + iy₂) = (x₁x₂ – y₁y₂) + i (x₁y₂ + x₂y₁)

• Division: Consider z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ be any two complex numbers, then their division is defined as

$\dfrac{z_1}{z_2}=\dfrac{x_1+iy_1}{x_2+iy_2}=\dfrac{(x_1x_2+y_1y_2)+i(x_2y_1-x_1y_2)}{x_2^2+y_2^2}\,\,\,\,\,\text{where}\,z_2\neq0.$

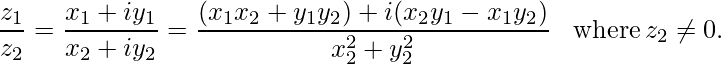
Conjugate of Complex Number

Consider z = x + iy, if ‘i’ is replaced by (-i), then it is called to be conjugate of the complex number z and it is denoted by z¯, i.e.

$\bar{z} = x - iy$

Modulus of a Complex Number

Consider z = x + y be a complex number. So, the positive square root of the sum of square of real part and square of imaginary part is called modulus (absolute values) of z and it is denoted by |z| i.e.

|z| = √x₂+y₂

Argand Plane

Any complex number z = x + y can be represented geometrically by a point (x, y) in a plane, called argand plane or gaussian plane. 

• A pure number x, i.e. (x + 0i) is represented by the point (x, 0) on X-axis. Therefore, X-axis is called real axis.
• A purely imaginary number y i.e. (0 + y) is represented by the point (0, y) on the y-axis. Therefore, the y-axis is called the imaginary axis.

Argument of a complex Number

The angle made by line joining point z to the origin, with the positive direction of X-axis in an anti-clockwise sense is called argument or amplitude of complex number. It is denoted by the symbol arg(z) or amp(z).

arg(z) = θ = tan^-1(y/x)

• Principal Value of Argument
  • When x > 0 and y > 0 ⇒ arg(z) = θ
  • When x < 0 and y > 0 ⇒ arg(z) = π – θ
  • When x < 0 and y < 0 ⇒ arg(z) = -(π – θ)
  • When x > 0 and y < 0 ⇒ arg(z) = -θ

Polar Form of a Complex Number

When z = x + iy is a complex number, so z can be written as, 

• z = |z| (cosθ + isinθ), where θ = arg(z).

which is known as the polar form. Now, when the general value of the argument is θ, so the polar form of z is written as,

• z = |z| [cos (2nπ + θ) + isin(2nπ + θ)], where n is an integer.

第 6 章：线性不等式

本章解释了线性不等式的概念。讨论的主题分别是一个变量和两个变量的线性不等式的代数解和图形表示。在数学中，不等式是两个不同值之间存在的关系，求解线性不等式与求解线性方程非常相似，除了一个小而重要的细节：只要将不等式乘以或除以一个否定的。

Inequation: An inequation or inequality is a statement involving variables and the sign of inequality like >, <, ≥ or ≤.

• Symbols used in inequalities
  • The symbol < means less than.
  • The symbol > means greater than.
  • The symbol < with a bar underneath ≤ means less than or equal to.
  • The symbol > with a bar underneath ≥ means greater than or equal to.
  • The symbol ≠ means the quantities on the left and right sides are not equal to.

Algebraic Solutions for Linear Inequalities in One Variable and its Graphical Representation

Using the trial-and-error method, the solution to the linear inequality can be determined. However, this method isn’t always possible, and computing the solution takes longer. So, using a numerical approach, the linear inequality can be solved. When solving linear inequalities, remember to follow these rules:

Rule 1: Don’t change the sign of an inequality by adding or subtracting the same integer on both sides of an equation.

Rule 2: Add or subtract the same positive integer from both sides of an inequality equation.

第 7 章：排列组合

本章解释了排列（以一定顺序排列多个对象）和组合（不考虑顺序的对象的集合）的概念。讨论的主题是计数、阶乘、排列、组合及其应用的基本原理以及受限排列的概念。如果某个事件以“m”个不同的方式发生，然后一个事件以“n”个不同的方式发生，则事件的发生总数可以按 m × n 顺序给出。找到第 11 类排列和组合的重要数学公式如下：

• Factorial: The continued product of first n natural number is called factorial ‘n’. It is denoted by n! which is given by,

n! = n(n – 1)(n – 2)… 3 × 2 × 1 and 0! = 1! = 1

• Permutations: Permutation refers to the various arrangements that can be constructed by taking some or all of a set of things. The number of an arrangement of n objects taken r at a time, where 0 < r ≤ n, denoted by ⁿP_r is given by

ⁿP_r = n! / (n−r)!

• The number of permutation of n objects of which p₁ are of one kind, p₂ are of second kind,… pk are of kth kind such that p₁ + p₂ + p₃ + … + p_k = n is

n! / p₁! p₂! p₃! ….. p_k!

• Combinations: Combinations are any of the various selections formed by taking some or all of a number of objects, regardless of their arrangement. The number of r objects chosen from a set of n objects is indicated by ⁿC_r, and it is given by

ⁿC_r = n! / r!(n−r)!

• Relation Between Permutation and combination: The relationship between the two concepts is given by two theorems as,
  • ⁿP_r = ⁿC_r r! when 0 < r ≤ n.
  • ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r

第8章：二项式定理

本章讨论用于解决复杂计算的正整数的二项式定理。讨论的主题是二项式定理的历史、陈述和证明及其扩展以及帕斯卡三角形。二项式定理有助于扩展给定任何正整数 n 的二项式。

• Binomial Theorem: The expansion of a binomial for any positive integer n is given by Binomial Theorem, which is

(a + b)ⁿ = ⁿC₀ a_n + ⁿC₁ a_n-1 b + ⁿC2 a_n-2 b₂ + … + ⁿC_n-1 a b_n-1 + ⁿC_n b_n

• Some special cases from the binomial theorem can be written as:
  • (x – y)ⁿ = ⁿC₀ x_n – ⁿC₁ x_n-1 y + ⁿC₂ x_n-2 y₂ + … + (-1)^{n n}C_n x_n
  • (1 – x)ⁿ = ⁿC₀ – ⁿC₁ x + ⁿC₂ x² – …. (-1)^{n n}C_n x_n
  • ⁿC₀ = ⁿC_n = 1
• Pascal’s triangle: The coefficients of the expansions are arranged in an array called Pascal’s triangle.
• General Term of following expansions are:
  • (a + b)ⁿ is T_r+1 = ⁿC_r a^n−r.b^r
  • (a – b)ⁿ is (-1)^{r n}C_r a^n−r.b^r
  • (1 + x)_n = ⁿC_r . x_r
  • (1 – x)_n = (-1)^{r n}C_n x^r
• Middle Terms: In the expansion (a + b)ⁿ, if n is even, then the middle term is the (n/2 + 1)^th term. If n is odd, then the middle terms are (n/2 + 1)^th and ((n+1)/2+1)^th terms.

第 9 章：序列和系列

数列和数列一章讨论数列（数字的有序列表）和数列（数列所有项的总和）的概念。讨论的主题是序列和级数、算术和几何级数、算术和几何平均数。以下是序列和序列中使用的一些重要术语的列表，如下所示：

• Progression: A sequence whose terms follow certain patterns is known as progression.
• Arithmetic Progression (AP): An arithmetic progression (A.P.) is a sequence where the terms either increase or decrease regularly by the same constant. This constant is called the common difference (d). The first term is denoted by a and the last term of an AP is denoted by l.
  • For an Arithmetic Series: a, a+d, a+2d, a+3d, a+4d, …….a +(n-1)d
    • The first term: a₁ = a,
    • The second term: a₂ = a + d,
    • The third term: a₃ = a + 2d,
    • The nth term: a_n = a + (n – 1)d
    • nth term of an AP from the last term is a’_n =a_n – (n – 1)d.
    • a_n + a’_n = constant
    • Common difference of an AP i.e. d = a_n – a_n-1, ∀ n>1.
    • Sum of n Terms of an AP: S_n = n/2 [2a + (n – 1)d] = n/2 (a₁+ a_n)
• A sequence is an AP If the sum of n terms is of the form An² + Bn, where A and B are constant and A = half of common difference i.e. 2A = d.

a_n =S_n – S_n-1

• Arithmetic Mean: If a, A and b are in A.P then A = (a+b)/2 is called the arithmetic mean of a and b. If a₁, a₂, a₃,……a_n are n numbers, then their arithmetic mean is given by: $A = \dfrac{a_1+a_2+a_3+...+a_n}{n}$
  • The common difference is given as, d = (b – a)/(n + 1)
  • The Sum of n arithmetic mean between a and b is, n (a+b/2).
• Geometric Progression (GP): A sequence in which the ratio of two consecutive terms is constant is called geometric progression.
  • The constant ratio is called common ratio (r).
    i.e. r = a_n+1/a_n, ∀ n>1
  • The general term or nth term of GP is a_n =ar^n-1
  • nth term of a GP from the end is a’_n = 1/r^n-1, l = last term
  • If a, b and c are three consecutive terms of a GP then b² = ac.
• Geometric Mean (GM): If a, G and b are in GR then G is called the geometric mean of a and b and is given by G = √(ab).
  • If a,G₁, G₂, G₃,….. G_n, b are in GP then G₁, G₂, G₃,……G_n are in GM’s between a and b, then
    common ratio is: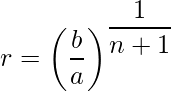 $r = \left(\dfrac{b}{a}\right)^{\dfrac{1}{n+1}}$
  • If a₁, a₂, a₃,…, a_n are n numbers are non-zero and non-negative, then their GM is given by
    GM = (a₁ . a₂ . a₃ …a_n)^1/n
  • Product of n GM is G₁ × G₂ × G₃ ×… × G_n = G_n = (ab)^n/2
• Sum of first n natural numbers is: Σn = 1 + 2 + 3 +… + n = n(n+1)/2
• Sum of squares of first n natural numbers is: Σn² = 1² + 2² + 3² + … + n² = n(n+1)(2n+1)/6
• Sum of cubes of first n natural numbers is: Σn³ = 1³ + 2³ + 3³ + .. + n³ = (n(n+1)(2n+1)/6)²

第10章：直线

直线定义了线的概念、它的角度、斜率和一般方程。讨论的主题分别是直线的斜率、两条直线之间的角度、各种形式的直线方程、直线的一般方程和直线族。以下是直线章节中使用的一些重要公式：

• Distance Formula: The distance between two points A(x₁, y₁) and B (x₂, y₂) is given by,

$AB = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$

• The distance of a point A(x, y) from the origin 0 (0, 0) is given by OA = √(x² + y²).
• Section Formula: The coordinates of the point which divides the joint of (x₁, y₁) and (x₂, y₂) in the ratio m:n internally, is

$\left(\dfrac{mx_2+nx_1}{m+n},\,\dfrac{my_2+ny_1}{m+n}\right)$

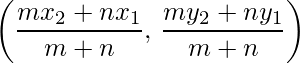
And externally is:

$\left(\dfrac{mx_2-nx_1}{m-n},\,\dfrac{my_2-ny_1}{m-n}\right)$

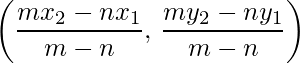
• Mid-Point of the joint of (x₁, y₁) and (x₂, y₂) is: $\left(\dfrac{x_1+x_2}{2},\,\dfrac{y_1+y_2}{2}\right)$.
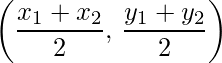  • X-axis divides the line segment joining (x₁, y₁) and (x₂, y₂) in the ratio -y₁ : y₂.
  • Y-axis divides the line segment joining (x₁, y₁) and (x₂, y₂) in the ratio -x₁ : x₂.
• Coordinates of Centroid of a Triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is

$\left(\dfrac{x_1+x_2+x_3}{3},\,\dfrac{y_1+y_2+y_3}{3}\right)$

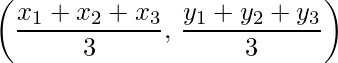
• Area of Triangle: The area of the triangle, the coordinates of whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) is,

$\begin{aligned}\text{Area of Triangle}&=\dfrac{1}{2}\begin{vmatrix}x_1&x_2&1\\x_2&y_2&1\\x_3&x_2&1\end{vmatrix}\\&=\dfrac{1}{2}\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right]\end{aligned}$

• If the points (x₁, y₁), (x₂, y₂) and (x₃, y₃) are collinear, then x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂) = 0.
• Slope or Gradient of Line: The inclination of angle θ to a line with a positive direction of X-axis in the anti-clockwise direction, the tangent of angle θ is said to be slope or gradient of the line and is denoted by m. i.e.

m = tan θ

• The slope of a line passing through points P(x₁, y₁) and Q(x₂, y₂) is given by,

$m = \text{tan}\theta=\dfrac{y_2-y_1}{x_2-x_1}$

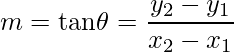
• Angle between Two Lines: The angle θ between two lines having slope m₁ and m₂ is, $\text{tan}\theta=\left|\dfrac{m_2-m_1}{1+m_1m_2}\right|$
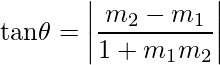
  • If two lines are parallel, their slopes are equal i.e. m₁ = m₂.
  • If two lines are perpendicular to each other, then their product of slopes is -1 i.e. m₁m₂ = -1.
• Point of intersection of two lines: Let equation of lines be ax₁ + by₁ + c₁ = 0 and a₂x + b₂y + c₂ = 0, then their point of intersection is

$\left(\dfrac{b_1c_2-b_2c_1}{a_1b_2-a_2b_1},\,\dfrac{a_2c_1-a_1c_2}{a_1b_2-a_2b_1}\right)$

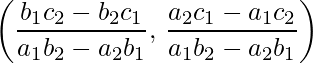
• Distance of a Point from a Line: The perpendicular distanced of a point P(x₁, y₁)from the line Ax + By + C = 0 is given by,

$d=\left|\dfrac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}\right|$

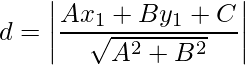
• Distance Between Two Parallel Lines: The distance d between two parallel lines y = mx + c₁ and y = mx + c₂ is given by,

$d=\dfrac{\left|c_1-c_2\right|}{\sqrt{1+m^2}}$

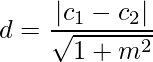
• Different forms of Equation of a line:
  • If a line is at a distance k and parallel to X-axis, then the equation of the line is y = ± k.
  • If a line is parallel to Y-axis at a distance of c from the Y-axis, then its equation is x = ± c.
  • General Equation of a Line: Any equation of the form Ax + By + C = 0, where A and B are simultaneously not zero is called the general equation of a line
  • Normal form: The equation of a straight line upon which the length of the perpendicular from the origin is p and angle made by this perpendicular to the x-axis is α, is given by: x cos α + y sin α = p.
  • Intercept form: The equation of a line that cuts off intercepts a and b respectively on the x and y-axes is given by: x/a + y/b = 1.
  • Slope-intercept form: The equation of the line with slope m and making an intercept c on the y-axis, is y = mx + c.
    • One point-slope form: The equation of a line that passes through the point (x₁, y₁) and has the slope of m is given by y – y₁ = m (x – x₁).
    • Two points form: The equation of a line passing through the points (x₁, y₁) and (x₂, y₂) is given by

$y-y_1=\left(\dfrac{y_2-y_1}{x_2-x_1}\right)(x-x_1)$

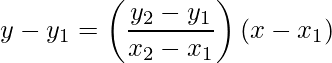
第 11 章：圆锥曲线

圆锥截面一章中讨论的主题是圆锥的截面，圆锥截面的退化情况沿着圆锥截面的方程和性质。圆是一个几何图形，其中平面中的所有点与给定平面上的固定点等距。以下是圆锥曲线一章中讨论的一些重要公式的列表：

• Equation of a circle with radius r having a centre (h, k) is given by (x – h)² + (y – k)² = r².
  • The general equation of the circle is given by x² + y² + 2gx + 2fy + c = 0 , where, g, f and c are constants.
  • The centre of the circle is (-g, -f).
  • The radius of the circle is r = √(g² + f² − c)
  • The parametric equation of the circle x² + y² = r² are given by x = r cos θ, y = r sin θ, where θ is the parameter.
  • And the parametric equation of the circle (x – h)² + (y – k)² = r² are given by x = h + r cos θ, y = k + r sin θ.
• Parabola: A parabola is the set of points P whose distances from a fixed point F in the plane are equal to their distance from a fixed-line l in the plane. The fixed point F is called focus and the fixed-line l is the directrix of the parabola.

Different forms of parabola	y2= 4ax	y2 = -4ax	x2 = 4ay	x2 = -4ay
Axis of parabola	y = 0	y = 0	x = 0	x = 0
Directrix of parabola	x = -a	x = a	y = -a	y = a
Vertex	(0, 0)	(0, 0)	(0, 0)	(0, 0)
Focus	(a, 0)	(-a, 0)	(0, a)	(0, -a)
Length of latus rectum	4a	4a	4a	4a
Focal length	|x + a|	|x – a|	|y + a|	|y – a|

• Ellipse: An ellipse is the set of all points in the plane whose distances from a fixed point in the plane bears a constant ratio, less than to their distance from a fixed point in the plane. The fixed point is called focus, the fixed line a directrix and the constant ratio (e) the eccentricity of the ellipse. The two standard forms of ellipse with their terminologies are mentioned below in the table:

Different forms of Ellipse	x2/a2 + y2/b2= 1, a > b	x2/b2 + y2/a2= 1, a > b
Equation of Major Axis	y = 0	x = 0
Length of Major Axis	2a	2a
Equation of Minor Axis	x = 0	y = 0
Length of Minor Axis	2b	2b
Equation of Directrix	x = ±a/e	y = ±a/e
Vertex	(±a, 0)	(0, ±a)
Focus	(±ae, 0)	(0, ±ae)
Length of latus rectum	2b2/a	2b2/a

• Hyperbola: A hyperbola is the locus of a point in a plane which moves in such a way that the ratio of its distance from a fixed point in the same plane to its distance from a fixed line is always constant which is always greater than unity. The fixed point is called the focus, the fixed line is called the directrix and the constant ratio, generally denoted bye, is known as the eccentricity of the hyperbola. The two standard forms of hyperbola with their terminologies are mentioned below in the table:

Different forms of Hyperbola	x2/a2 – y2/b2= 1	x2/a2 – y2/b2= 1
Coordinates of centre	(0, 0)	(0, 0)
Coordinates of vertices	(±a, 0)	(0, ±a)
Coordinates of foci	(±ae, 0)	(0, ±ae)
Length of Conjugate axis	2b	2b
Length of Transverse axis	2a	2a
Equation of Conjugate axis	x = 0	y = 0
Equation of Transverse axis	y = 0	x = 0
Equation of Directrix	x = ±a/e	y = ±a/e
Eccentricity (e)	√(a2+b2)/a2	√(a2+b2)/a2
Length of latus rectum	2b2/a	2b2/a

第 12 章：三维几何简介

顾名思义，本章解释了三维空间中的几何概念。讨论的主题分别是坐标轴和平面，点坐标，距离和点的截面。由这对轴确定的三个平面称为坐标平面，具有 XY、YZ 和 ZX 平面。在下面找到第 11 课《三维几何概论》的重要数学公式：

• Coordinate Axes: In three dimensions, the coordinate axes of a rectangular cartesian coordinate system are three mutually perpendicular lines. These axes are called the X, Y and Z axes.
• Coordinate Planes: The three planes determined by the pair of axes are the coordinate planes. These planes are called XY, YZ and ZX planes and they divide the space into eight regions known as octants.
• Coordinates of a Point in Space: The coordinates of a point in the space are the perpendicular distances from P on three mutually perpendicular coordinate planes YZ, ZX, and XY respectively. The coordinates of a point P are written in the form of triplet like (x, y, z). The coordinates of any point on:
  • X-axis is of the form (x, 0,0)
  • Y-axis is of the form (0, y, 0)
  • Z-axis is of the form (0, 0, z)
  • XY-plane are of the form (x, y, 0)
  • YZ-plane is of the form (0, y, z)
  • ZX-plane are of the form (x, 0, z)
• Distance Formula: The distance between two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) is given by,

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$

• While, the distance between two points A(x, y, z) from the origin O(0, 0, 0) is given by,

$OA=\sqrt{x^2+y^2+z^2}$

• Section Formula: The coordinates of the point R which divides the line segment joining two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) internally or externally in the ratio m : n are given by,

$\left(\dfrac{mx_2+nx_1}{m+n},\dfrac{my_2+ny_1}{m+n},\dfrac{mz_2+nz_1}{m+n}\right)\,\text{and}\left(\dfrac{mx_2-nx_1}{m-n},\dfrac{my_2-ny_1}{m-n},\dfrac{mz_2-nz_1}{m-n}\right)$

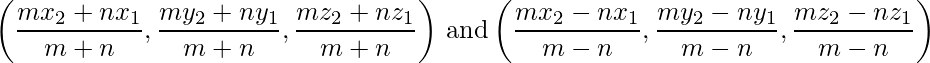
• Mid-Point of the joint of (x₁, y₁) and (x₂, y₂) is:

$\left(\dfrac{x_1+x_2}{2},\,\dfrac{y_1+y_2}{2}\right)$

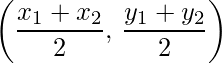
• Coordinates of Centroid of a Triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is

$\left(\dfrac{x_1+x_2+x_3}{3},\,\dfrac{y_1+y_2+y_3}{3}\right)$

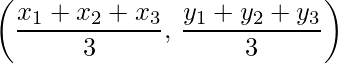
第 13 章：极限和导数

本章解释了微积分的概念，该概念涉及当域点发生变化时函数值的变化研究。讨论的主题分别是极限和导数的定义和代数运算。

函数在某一点的极限具有一个共同的值，如果它们彼此重合，则它们具有左极限和右极限。以下是一些用于解决极限和导数问题的重要公式列表，

• Limit: Let y = f(x) be a function of x. If at x = a, f(x) takes indeterminate form, then we consider the values of the function which is very near to a. If these value tend to a definite unique number as x tends to a, then the unique number so obtained is called the limit of f(x) at x = a and we write it as $\lim_{x\to a}f(x)$.
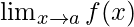• Left Hand and Right-Hand Limits: If values of the function at the point which are very near to a on the left tends to a definite unique number as x tends to a, then the unique number so obtained is called the left-hand limit of f(x) at x = a, we write it as

$f(a-0)=\lim_{x\to a^-}f(x)=\lim_{h\to 0}f(a-h)$

• Similarly, right hand limit is given as,

$f(a+0)=\lim_{x\to a^+}f(x)=\lim_{h\to 0}f(a+h)$

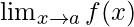• A limit $\lim_{x\to a}f(x)$ exists when:

$\lim_{x\to a^-}f(x)$ and $\lim_{x\to a^+}f(x)$ both exists or,

$\lim_{x\to a^-}f(x) = \lim_{x\to a^+}f(x)$

• Some Important Properties of Limits: Consider f and g be two functions such that both \lim_{x\to a}f(x) and \lim_{x\to a}g(x) exists, then:

$\begin{aligned}\lim_{x\to a}[f(x)\pm g(x)]&=\lim_{x\to a}f(x)\pm \lim_{x\to a} g(x)\\\lim_{x\to a}kf(x)&=k\lim_{x\to a}f(x)\\\lim_{x\to a}f(x)\cdot g(x)&=\lim_{x\to a}f(x)\times\lim_{x\to a}g(x)\\\lim_{x\to a}\dfrac{f(x)}{g(x)}&=\dfrac{\lim_{x\to a}f(x)}{\lim_{x\to a}g(x)}\end{aligned}$

• Some Standard Limits are given as:

$\begin{aligned}\lim_{x\to a}\dfrac{x^n-a^n}{x-a}&=na^{n-1}\\\lim_{x\to 0}\dfrac{\sin x}{x}&=1\\\lim_{x\to 0}\dfrac{\tan x}{x}&=1\\\lim_{x\to 0}\dfrac{a^x-1}{x}&=\log_e a\\\lim_{x\to 0}\dfrac{e^x-1}{x}&=1\\\lim_{x\to 0}\dfrac{\log(1+x)}{x}&=1\end{aligned}$ 

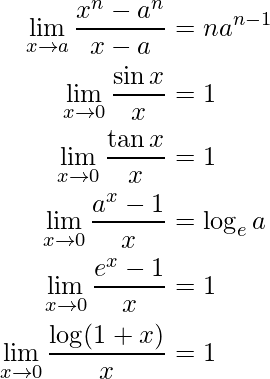
• Derivatives: Consider a real-valued function f, such that:

$f'(x)=\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$ 

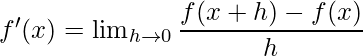
is known as the Derivative of function f at x if and only if,

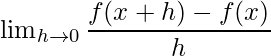$\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$ exists finitely.

• Some Important Properties of Derivatives: Consider f and g be two functions such that their derivatives can be defined in a common domain as:

$\begin{aligned}\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)+g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]+\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)-g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]-\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)\cdot g(x)]&=\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)+f(x)\cdot\left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]\\\dfrac{\mathrm{d}}{\mathrm{d}x}\left[\dfrac{f(x)}{g(x)}\right]&=\dfrac{\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)-f(x)\cdot \left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]}{[g(x)]^2}\end{aligned}$

• Some Standard Derivatives are given as:

$\begin{aligned}\dfrac{\mathrm{d}}{\mathrm{d}x}(x^n)&=nx^{n-1}\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\sin x)&=\cos x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\cos x)&=-\sin x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\tan x)&=\sec^2 x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\cot x)&=-\cosec^2 x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\sec x)&=\sec x \tan x\\\dfrac{\mathrm{d}}{\mathrm{d}x}\cosec x&=-\cosec x \cot x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(a^x)&=a^x\log_e a\\\dfrac{\mathrm{d}}{\mathrm{d}x}(e^x)&=e^x\\\dfrac{\mathrm{d}}{\mathrm{d}x}(\log_e x)&=\dfrac{1}{x}\end{aligned}$

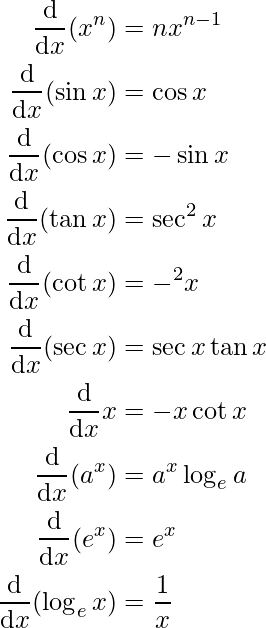
第14章：数学推理

顾名思义，本章解释了数学推理的概念（在数学背景下分析任何给定假设的关键技能）。讨论的主题是陈述、归纳推理和演绎推理。以下是讨论的重要术语列表：

• Statements: A statement is a sentence which either true or false, but not both simultaneously. For example: “A triangle has four sides.”, “New Delhi is the capital of India.” are the statements.
• Negation of a statement: Negation of a statement p: If p denote a statement, then the negation of p is denoted by ∼p.
• Compound statement: A statement is a compound statement if it is made up of two or more smaller statements. The smaller statements are called component statements of the compound statement. The Compound statements are made by:
  • Connectives: “AND”, “OR”
  • Quantifiers: “there exists”, “For every”
  • Implications: The meaning of implications “If ”, “only if ”, “ if and only if ”.
• “p ⇒ q” : 
  • p is a sufficient condition for q or p implies q.
  • q is necessary to condition for p. The converse of a statement p ⇒ q is the statement q ⇒ p.
  • p⇒ q together with its converse gives p if and only if q.
• “p ⇔ q”:
  • p implies q (denoted by p ⇒ q)
  • p is a sufficient condition for q
  • q is a necessary condition for p
  • p only if q
  • ∼q implies ∼p
• Contrapositive: The contrapositive of a statement p ⇒ q is the statement ∼ q ⇒∼p.
• Contradiction: If to check whether p is true we assume negation p is true.
• Validating statements: Checking of a statement whether it is true or false. The validity of a statement depends upon which of the special. The following methods are used to check the validity of statements:
  • direct method
  • contrapositive method
  • method of contradiction
  • using a counterexample.

第 15 章：统计

本章解释了统计（为特定目的收集的数据）、离散度以及未分组和分组数据的计算方法的概念。讨论的主题是范围、平均偏差、方差和标准偏差，以及频率分布分析。在这里可以找到下面给出的第 11 级统计的基本数学公式：

• Measure of Dispersion: The dispersion is the measure of variations in the values of the variable. It measures the degree of scatteredness of the observation in a distribution around the central value.
• Range: The measure of dispersion which is easiest to understand and easiest to calculate is the range. Range is defined as the difference between two extreme observation of the distribution.

Range of distribution = Largest observation – Smallest observation.

• Mean Deviation: 

Mean deviation for ungrouped data- For n observations x₁, x₂, x₃,…, x_n, the mean deviation about their mean x¯ is given by:

$MD(\bar x)=\dfrac{\sum |x_i - \bar x|}{n}$

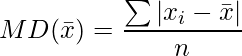
And, the Mean deviation about its median M is given by,

$MD(M)=\dfrac{\sum |x_i - M|}{n}$

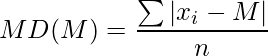
Mean deviation for discrete frequency distribution- 

$MD(\bar x)=\dfrac{\sum f_i|x_i - \bar x|}{\sum f_i}=\dfrac{\sum f_i|x_i - \bar x|}{N}$

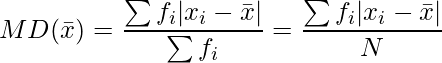
Variance: Variance is the arithmetic mean of the square of the deviation about mean x¯.
Let x₁, x₂, ……x_n be n observations with x¯ as the mean, then the variance denoted by σ², is given by

$\sigma^2=\dfrac{\sum(x_i-\bar x)^2}{n}$

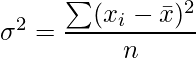
Standard deviation: If σ² is the variance, then σ is called the standard deviation is given by

$\sigma=\sqrt{\dfrac{\sum(x_i-\bar x)^2}{n}}$

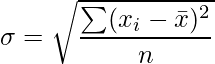
Standard deviation of a discrete frequency distribution is given by

$\sigma=\sqrt{\dfrac{\sum f_i(x_i-\bar x)^2}{N}}$

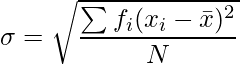
Coefficient of variation: In order to compare two or more frequency distributions, we compare their coefficient of variations. The coefficient of variation is defined as

Coefficient of variation = (Standard deviation / Mean) × 100

$CV=\dfrac{\sigma}{\bar x}\times 100$

第16章：概率

概率是 11 年级数学课程的基本组成部分，对于 11 年级考试和 JEE 和 NEET 等不同的竞争性考试很重要。在以前的课程中，学生可能已经学习了概率的基本概念，作为衡量各种现象的不确定性。在这里，讨论了公式列表、重要性质、应用和章节摘要，有助于学生快速学习相关概念并在考试中取得好成绩。

本章讨论概率的概念（衡量各种现象的不确定性或事件发生的机会）。讨论的主题是随机实验、结果、样本空间、事件及其类型。以下是第 11 类概率的重要公式列表和章节摘要：

• Probability = Number of Favourable outcomes in an Event / Total number of Outcomes
• Event: An event is a subset of the S (sample space). An empty set is also known as the Impossible event.
  • For any random experiment, let S be the sample space. The probability P is a real-valued function whose domain is the power set of S and [0, 1] is the range interval. For any event E: P(E) ≥ 0 and P(S) = 1
  • Mutually exclusive events: If E and F are mutually exclusive events, then: P(E ∪ F) = P(E) + P(F)
  • Equally likely outcomes: All outcomes with equal probability are called equally likely outcomes. Let S be a finite sample space with equally likely outcomes and A be the event. Therefore, the probability of an event A is: P(A) = n(A) / n(S), where n(A) is the number of elements on the set A and n(S) is the Total number of outcomes or the number of elements in the sample space S
• Let P and Q be any two events, then the following formulas can be derived.
  • Event P or Q: The set P ∪ Q
  • Event P and Q: The set P ∩ Q
  • Event P and not Q: The set P – Q
  • P and Q are mutually exclusive if P ∩ Q = φ
  • Events P₁, P₂, . . . . . , P_n are exhaustive and mutually exclusive if P₁ ∪ P₂ ∪ . . . . . ∪ P_n = S and E_i ∩ E_j = φ for all i ≠ j.