CBSE 9 级数学公式

GeeksforGeeks 为 9 年级提供数学分章公式。这是为了方便学生而设计的，以便学生可以直接轻松地理解 9 年级数学的所有重要概念。这里提供了第 9 班的数学公式，供那些发现数学主题是一场噩梦且难以掌握的学生使用。因此，他们可能会变得犹豫不决并失去对学习的兴趣。因此，GeeksforGeeks 提到了第 9 个标准数学教学大纲的所有关键公式，学生可以简单地回忆起来，以帮助他们轻松理解数学。对于代数、几何、多项式等所有课程，此处根据 NCERT 课程提供公式。

第 1 章：数字系统

数字或数系是自然数、整数、有理数、无理数和实数的组合。本课涵盖了数字系统及其类型的全部概念、数轴上的表示、有理指数定律和积分幂。任何可以表示为 p ⁄ q 的数，其中 p 和 q 是整数，q ≠ 0 是有理数。 p ⁄ q 形式不能用于写无理数。

• Any unique real number can be represented on a number line.
• If r is one such rational number and s is an irrational number, then (r + s), (r – s), (r × s) and (r ⁄ s) are irrational.
• Following rules must hold for positive real numbers:
  1. √ab = √a × √b
  2. √(a/b)= √a/√b
  3. (√a + √b) × (√a – √b) = a−b
  4. (a + √b) × (a − √b) = a² −b
  5. (√a+√b)² =a² + 2√ab +b
• To rationalize the denominator of 1 ⁄ √ (a + b), then one must have to multiply it by √(a – b) ⁄ √(a – b), where a and b are both the integers.
• Suppose a is a real number (greater than 0) and p and q are the rational numbers.
  1. a^p × b^q = (ab)^p+q
  2. (a^p)^q = a^pq
  3. a^p / a^q = (a)^p-q
  4. a^p / b^p = (ab)^p

第 2 章：多项式

多项式是包含变量和系数的表达式，其中涉及变量的加法、减法、乘法和非负整数取幂等操作。表示一个变量“x”的多项式 p(x) 包含以下形式的代数表达式：

p(x) = a_nxⁿ + a_n-1x^n-1 + ….. + a₂x² + a₁x + a₀ 

where a₀, a₁, a₂, …. a_n are constants where a_n ≠ 0

1. Any real number; let’s say ‘a’ is considered to be the zero of a polynomial ‘p(x)’ if p(a) = 0. In this case, a is said to be the equation p(x) = 0.
2. Every one variable linear polynomial will contain a unique zero, a real number which is a zero of the zero polynomial, and a non-zero constant polynomial that does not have any zeros.
3. Remainder Theorem: If p(x) has the degree greater than or equal to 1 and p(x) when divided by the linear polynomial x – a will give the remainder as p(a).
4. Factor Theorem: x – a will be the factor of the polynomial p(x), whenever p(a) = 0. The vice-versa also holds true every time.

第 3 章：坐标几何

坐标几何是几何的一部分，其中点在平面上的位置是借助称为坐标的有序数字对来描述的。

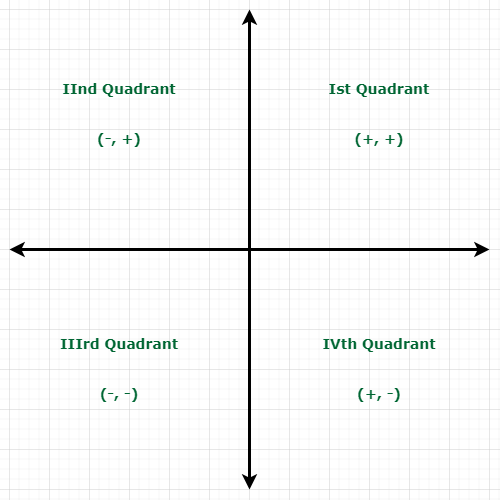
坐标几何：象限

Whenever you have to locate an object on a plane, you need two divide the plane into two perpendicular lines, thereby, making it a Cartesian Plane.

1. The horizontal line is known as the x-axis and the vertical line is called the y-axis.
2. The coordinates of a point are in the form of (+, +) in the first quadrant, (–, +) in the second quadrant, (–, –) in the third quadrant, and (+, –) in the fourth quadrant; where + and – denotes the positive and the negative real number respectively.
3. The coordinates of the origin are (0, 0) and thereby it gets up to move in the positive and negative numbers.

第 4 章：两变量线性方程组

任何可以用 ax + by + c = 0 的形式定义的方程，其中 a、b 和 c 是实数，并且 a 和 b 不都是零，称为二元线性方程。下面给出了代数恒等式，它们被认为是第 9 课非常重要的数学公式。

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b) (a – b) = a² -b²
• (x + a) (x + b) = x² + (a + b) x + ab
• (x + a) (x – b) = x² + (a – b) x – ab
• (x – a) (x + b) = x² + (b – a) x – ab
• (x – a) (x – b) = x² – (a + b) x + ab
• (a + b)³ = a³ + b³ + 3ab (a + b)
• (a – b)³ = a³ – b³ – 3ab (a – b)
• (x + y + z)² = x² + y² + z² + 2xy +2yz + 2xz
• (x + y – z)² = x² + y² + z² + 2xy – 2yz – 2xz
• (x – y + z)² = x² + y² + z² – 2xy – 2yz + 2xz
• (x – y – z)² = x² + y² + z² – 2xy + 2yz – 2xz
• x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz -xz)
• x² + y² =  1212 [(x + y)² + (x – y)²]
• (x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc
• x³ + y³ = (x + y) (x² – xy + y²)
• x³ – y³ = (x – y) (x² + xy + y²)
• x² + y² + z² – xy – yz – zx = 1212 [(x – y)² + (y – z)² + (z – x)²]

第 5 章：欧几里得几何导论

欧几里得几何是几何的一个分支，它处理基于不同公理和定理的几何形状和图形的研究。这项研究基本上提供了平面的简要说明。

• Axioms: The basic facts which are taken for granted without proof are called axioms. Some of Euclid’s axioms are:
  1. Things which are equal to the same thing are equal to one another.
  2. If equals are added to equals, the wholes are equal.
  3. If equals are subtracted from equals, the remainders are equal.
  4. Things which coincide with one another are equal to one another.
  5. The whole is greater than the part.
• Postulates: Axioms are the general statements, postulates are the axioms relating to a particular field. Euclid’s five postulates are.
  1. A straight line may be drawn from anyone point to any other point.
  2. A terminated line can be produced indefinitely.
  3. A circle can be drawn with any center and any radius.
  4. All right angles are equal to one another.
  5. If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely meet on that side on which the angles are less than two right angles.

第 6 章：线和角

这里提供了第 9 类音符的重要公式和一些音符点。这里简要解释了各种概念，例如平行线，横截面，角度，相交线，内角。

• Angle: The union of two non-collinear rays with a shared beginning point is called an angle.
• Types of Angles: Following are the major types of angles-
  • Acute angle: An acute angle measure between 0° and 90°.
  • Right angle: A right angle is exactly equal to 90°.
  • Obtuse angle: An angle greater than 90° but less than 180°.
  • Straight angle: A straight angle is equal to 180°. Reflex angle: An angle that is greater than 180° but less than 360° is called a reflex angle.
  • Complementary angles: Two angles whose sum is 90° are called complementary angles. Let one angle be x, then its complementary angle is (90°−x).
  • Supplementary angles: Two angles whose sum is 180° are called supplementary angles. Let one angle be x, then its supplementary angle is (180°−x).
  • Adjacent angles: Two angles are Adjacent when they have a common side and a common vertex (corner point) and don’t overlap.
  • Linear pair: A linear pair of angles is formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines. The measure of a straight angle is 180°, so a linear pair of angles must add up to 180°.
  • Vertically opposite angles: Vertically opposite angles are formed when two lines intersect each other at a point. Vertically opposite angles are always equal.
  • Transversal: A line that intersects two or more given lines at distinct points, is called a transversal of the given line. Following are the angles that are made on a traversal as,
    1. Corresponding angles
    2. Alternate interior angles
    3. Alternate exterior angles
    4. Interior angles on the same side of the transversal.

第 7 章：三角形

正如几何学所描述的，三角形是具有三个边和三个顶点的三边多边形。三角形的角和特性是最重要和最广泛使用的特性，它表明三角形的内角和只有 180 度。三个边和三个角组成一个三角形，是一个封闭的几何对象。

• Congruence: Congruent refers to figures that are identical in all aspects, such as their forms and sizes. Two circles with the same radii, for example, are congruent. Also congruent are two squares with the same sides.
• Congruent Triangles: Two triangles are congruent if and only if one of them can be superimposed over the other to entirely cover it.
• Congruence Rules: Following are the list of some important congruence rules of triangles,
  • Side angle side (SAS) Congruence
  • Angle Side Angle (ASA) Congruence
  • Angle angle side (AAS) Congruence
  • Side side side (SSS) Congruence
  • Right-angle Hypotenuse Side (RHS) Congruence

第8章：四边形

四边形是一个平面几何图形，它有四个边，有四个角或顶点。通常，四边形是矩形、正方形、梯形和风筝形或不规则且无特征的具有四个边的图形。以下是有关四边形一章的一些重要属性和简短说明：

• The Sum of all angles of a quadrilateral is 360°.
• A diagonal of a parallelogram divides it into two congruent triangles.
• In a parallelogram,
  • diagonals bisect each other.
  • opposite angles are equal.
  • opposite sides are equal
• Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
• A line through the mid-point of a side of a triangle parallel to another side bisects the third side. (Midpoint theorem)
• The line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the third side.
• In a parallelogram, the bisectors of any two consecutive angles intersect at a right angle.
• If a diagonal of a parallelogram bisect one of the angles of a parallelogram it also bisects the second angle.
• The angle bisectors of a parallelogram form a rectangle.
• Each of the four angles of a rectangle is the right angle.
• The diagonals of a rhombus are perpendicular to each other.

第 9 章：平行四边形和三角形的面积

平面图形的面积描述为矩形、正方形等封闭几何图形所覆盖的平面面积。平行四边形是一种包含平行对边的四边形。下面提到的是在平行四边形和三角形区域中使用的公式列表，

1. Area of Parallelogram = Base × Height
2. Area of Triangle = 1/2 × Base × Height or 1/2 × Area of Parallelogram
3. Area of Trapezium = 1/2 × (Sum of its parallel sides) × Distance between the two parallel side
4. Area of Rhombus = 1/2 × Product of its two diagonals

第 10 章：圆圈

在距中心等距距离处绘制的点的轨迹称为圆。圆的半径是圆心到外线的距离。圆的直径是把它分成两个相等部分的线，它等于半径的两倍。因此，在第 9 类教学大纲中，讨论了与圆相关的以下重要属性和公式：

• Concentric circles are circles with the same center but different radii.
• Arc: An arc of the circle is a continuous portion of a circle.
• Chord: The chord of the circle is a line segment that connects any two locations on a circle. Some important properties of Chords of a circle are:
  • The diameter of a circle is defined as a chord that passes across its center.
  • A circle’s diameter divides it into two equal sections, which are called arcs. A semi-circle is made up of these two arcs.
  • If two arcs of a circle have the same degree of measure, they are said to be congruent.
  • When two arcs have the same length, their associated chords are likewise the same length.
  • The chord is bisected by a perpendicular drawn from the center to the chord of the circle, and vice versa.
  • Three non-collinear points are intersected by one and only one circle.
  • Equal circle chords are equidistant from the center.
  • The line across the centers of two circles intersecting in two points is perpendicular to the common chord.
  • An arc’s angle at the center of the circle is double the angle it has throughout the rest of the circumference.
  • Any two angles in the same circle segment are equal.
  • A circle’s equal chords form an equal angle at the center.
  • The greater chord of a circle is closer to the center than the smaller chord.
  • The semicircle has a right angle. At the circle’s center, equal chords subtend an equal angle.
• Cyclic Quadrilateral: A quadrilateral is said to be cyclic if all of its vertices are on the perimeter of a circle.
  • The sum of opposing angles in a cyclic quadrilateral is 180°, and vice versa.
  • A cyclic quadrilateral’s exterior angle is equal to its inner opposite angle.

第 11 章：结构

构造类 9 的第 11 章演示了如何用圆规和尺子设计各种形式。本章解释如何创建给定角度的平分线，以及如何制作给定线段的垂直平分线，使用施工阶段和清晰的图片。要获得高分，您还应该能够学习教材中关于第 9 课数学第 11 章构造问题的所有相关问题。以下是构建重要几何图形的不同规则：

• Construction of bisector of a line segment
• Construction of bisector of a given angle
• Construction of Equilateral triangle
• Construction of a triangle when its base, sum of the other two sides and one base angle are given
• Construction of a triangle when its base, difference of the other two sides and one base angle are given
• Construction of a triangle of given perimeter and two base angles

第12章：赫伦公式

三角形是几何中的封闭三维形状。在这里，学生可以找到在第 9 班教学大纲中研究的苍鹭公式及其重要应用。海伦公式用于计算三角形的面积。以下是苍鹭公式及其一些重要应用的列表：

• The semi-perimeter of a Triangle, s = (a+b+c)/2
• Area of the triangle = √{s(s−a)(s−b)(s−c)} sq. unit.
• For an Equilateral Triangle with side a:
  • Its Perimeter = 3a units
  • Its Altitude = √3/2 a units
  • Its Area = √3/4 a² units

第 13 章：表面积和体积

表面积是第 9 类表面积和体积中最重要的子主题之一。当我们计算一个二维项目所占据的空间时，我们称之为面积，以平方为单位来衡量；然而，当我们计算一个三维物体所占据的空间时，我们称其为表面积并以平方为单位进行测量。有两种表面积：

1. Total Surface Area (TSA): The whole area covered by the object’s surface is called the Total Surface area. Following is the list of the total surface areas of some important geometrical figure-
   1. TSA of a Cuboid = 2(l x b) +2(b x h) +2(h x l)
   2. TSA of a Cube = 6a²
   3. TSA of a Right circular Cylinder = 2πr(h+r)
   4. TSA of a Right circular Cone = πr(l+r)
   5. TSA of a Sphere = 4πr²
2. Lateral/Curved Surface Area: The curved surface area is the area of only the curved component, or in the case of cuboids or cubes, it is the area of only four sides, excluding the base and top. It’s called the lateral surface area for forms like cylinders and cones.
   1. CSA of a Cuboid = 2h(l+b)
   2. CSA of a Cube = 4a²
   3. CSA of a Right circular Cylinder = 2πrh
   4. CSA of a Right circular Cone = πrl
3. Volume: The volume of an object or material is the amount of space it takes up, measured in cubic units. There is no volume in a two-dimensional object, only area. A circle’s volume cannot be calculated since it is a 2D figure, while a sphere’s volume can be calculated because it is a 3D figure.
   1. Volume of a Cuboid = l x b x h
   2. Volume of a Cube = a³
   3. Volume of a Right circular Cylinder = πr²h
   4. Volume of a Right circular Cone = 1/3πr²h
   5. Volume of a Sphere = 4/3πr³

Here, l is the length, b is the breadth, h is the height, r is the radius and a is the side of the respective geometrical figure.

第 14 章：统计

统计学是对数据的表示、收集、解释、分析、呈现和组织的研究。换句话说，它是一种收集、汇总数据的数学方法。数据的表示方式与频率分布不同。可以收集或转换为某些有用目的的某些事实或数据称为数据。这些数据可以用图形表示，以提高人们的可读性。以下是本章的简要总结：

• Class mark = (Lower Limit + Upper Limit)/2
• The three central tendencies are measured as:
  1. Mean (x‾) = Sum of all observations (∑x_n) / Total Number of observation (N)
  2. Median = The median for even number of observation is equal to the middlemost observation whole for the odd number of observation it is equal to value of ((n+1)/2)th observation.
  3. Mode = It is equal to observation which occurs the most or have the maximum frequency in the given data.

第15章：概率

本课程中的概率包括基本概率论，该理论也用于概率分布，用于学习随机实验结果的可能性，并在可能结果的总数时找出单个事件发生的概率。概率是任何可能发生的事件的可能性。任何事件的概率只能从 0 到 1，0 表示没有机会，1 表示该事件发生的可能性。

• Probability P (E) = Number of favorable outcomes / Total Number of outcomes
• The probability of any event only lies between 1 and 0.
• Trial: It is defined as the set of observations of event in which one or more outcomes are observed.
• Event: It is defined as the collection of observation performed to observe an experiment.