CBSE 10 级数学公式

GeeksforGeeks 提出的数学类 10 章节公式是章节公式列表以及章节摘要和重要定义的组合。众所周知，Class 10 是工程、医学、商业、金融、计算机科学、硬件等各个高等教育领域的每个学生的重要等级。几乎在每个行业中，Class 10 中引入的最常见的公式是用过的。这些 CBSE 数学第 10 课分章公式包括与数系统、多项式、三角学、代数、测量、概率和统计相关的所有公式。

因此，这篇文章对第 10 班非常有用，它将帮助考生在即将到来的 CBSE 董事会考试中取得好成绩。

第 1 章：实数

第 10 课的数学第一章将向您介绍各种概念，例如自然数、整数和实数等。让我们看一下第 1 章第 10 类实数的一些概念和公式：

• Types of Numbers:
  • Natural Numbers – It is the counting numbers that can be expressed as: N = {1, 2, 3, 4, 5 >.
  • Whole number – It is the counting numbers along with zero. Therefore, they are written as: W= {0, 1, 2, 3, 4, 5 >
  • Integers – These are the numbers that include all the numbers, positive numbers, zero, and negative numbers also i.e.  ……-4,-3,-2,-1,0,1,2,3,4,5… so on.
    • Positive integers – These are: Z₊ = 1, 2, 3, 4, 5, ……
    • Negative integers – These are: Z_– = -1, -2, -3, -4, -5, ……
  • Rational Number – The number which is expressed in the form p/q where p and q are integers and q is a positive integer. For example 3/7 etc.
  • Irrational Number – The number which can not be expressed in the form p/q. For example π, √5, etc.
  • Real Numbers – A number that can be found on the number line is referred to as a real number. The numbers we use and use in real-world applications are known as real numbers. Natural Numbers, Whole Numbers, Integers, Fractions, Rational Numbers, and Irrational Numbers are all examples of real numbers.
• Euclid’s Division Algorithm (lemma): According to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r such that a = bq + r, where 0 ≤ r ≤ b. (Here, a is the dividend, b is the divisor, q is the quotient, and r is the remainder.)
• The fundamental theorem of arithmetic said that the Composite Numbers are equal to the Product of Primes.
• HCF and LCM by prime factorization method:
  • HCF = Product of the smallest power of each common factor in the numbers
  • LCM = Product of the greatest power of each prime factor involved in the number
  • HCF (a,b) × LCM (a,b) = a × b

第 2 章：多项式

描述相等概念的数学表达式的研究称为代数。例如，多项式方程是最常见的涉及多项式的代数方程。在第 10 课中学习代数公式将帮助您将各种应用题转化为数学形式。学生一旦记住了这些公式，就可以很快学会识别方程式的类型并使用规则来解决它们。这些代数公式具有可以以多种方式解释的各种输入和输出。以下是第 10 类的所有关键代数公式和属性：

• The general Polynomial Formula is, F (x) = a_nxⁿ + bx^n-1 + a_n-2x^n-2 + …….. + rx + s
  • When n is a natural number: aⁿ – bⁿ = (a – b)(a^n-1 + a^n-2b +…+ b^n-2a + b^n-1)
  • When n is even (n = 2a): xⁿ + yⁿ = (x + y)(x^n-1 – x^n-2y +…+ y^n-2x – y^n-1)
  • When n is odd number: xⁿ + yⁿ = (x + y)(x^n-1 – x^n-2y +…- y^n-2x + y^n-1)
• Types of Polynomials: Here are some important concepts and propeties are mentioned in the below table for each type of polynomials-

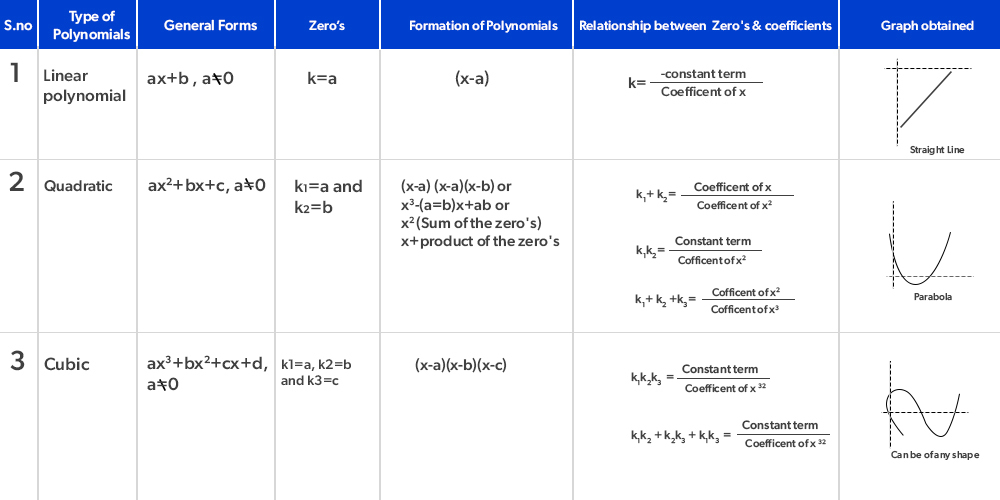
• Algebraic Polynomial Identities:
  1. (a+b)² = a² + b² + 2ab
  2. (a-b)² = a² + b² – 2ab
  3. (a+b) (a-b) = a² – b²
  4. (x + a)(x + b) = x² + (a + b)x + ab
  5. (x + a)(x – b) = x² + (a – b)x – ab
  6. (x – a)(x + b) = x² + (b – a)x – ab
  7. (x – a)(x – b) = x² – (a + b)x + ab
  8. (a + b)³ = a³ + b³ + 3ab(a + b)
  9. (a – b)³ = a³ – b³ – 3ab(a – b)
  10. (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2xz
  11. (x + y – z)² = x² + y² + z² + 2xy – 2yz – 2xz
  12. (x – y + z)² = x² + y² + z² – 2xy – 2yz + 2xz
  13. (x – y – z)² = x² + y² + z² – 2xy + 2yz – 2xz
  14. x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz -xz)
  15. x² + y² =½ [(x + y)² + (x – y)²]
  16. (x + a) (x + b) (x + c) = x³ + (a + b +c)x² + (ab + bc + ca)x + abc
  17. x³ + y³= (x + y) (x² – xy + y²)
  18. x³ – y³ = (x – y) (x² + xy + y²)
  19. x² + y² + z² -xy – yz – zx = ½ [(x-y)² + (y-z)² + (z-x)²]
• Division algorithm for polynomials: If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that

p(x) = q(x) × g(x) + r(x)

where r(x) = 0 or degree of r(x) < degree of g(x). Here p(x) is divided, g(x) is divisor, q(x) is quotient and r(x) is remainder.

第 3 章：两变量线性方程组

两个变量中的线性方程组是至关重要的一章，其中包含一系列重要的数学公式，适用于 10 年级，特别是对于竞争性考试。本章的一些重要概念如下：

• Linear Equations: An equation which can be put in the form ax + by + c = 0, where a, b and c are Pair of Linear Equations in Two Variables, and a and b are not both zero, is called a linear equation in two variables x and y
• Solution of a system of linear equations: The solution of the above system is the value of x and y that satisfies each of the equations in the provided pair of linear equations.
  1. Consistent system of linear equations: If a system of linear equations has at least one solution, it is considered to be consistent.
  2. Inconsistent system of linear equation: If a system of linear equations has no solution, it is said to be inconsistent.

S. No.	Types of Linear Equation	General form	Description	Solutions
1.	Linear Equation in one Variable	ax + b=0	Where a ≠ 0 and a & b are real numbers	One Solution
2.	Linear Equation in Two Variables	ax + by + c = 0	Where a ≠ 0 & b ≠ 0 and a, b & c are real numbers	Infinite Solutions possible
3.	Linear Equation in Three Variables	ax + by + cz + d = 0	Where a ≠ 0, b ≠ 0, c ≠ 0 and a, b, c, d are real numbers	Infinite Solutions possible

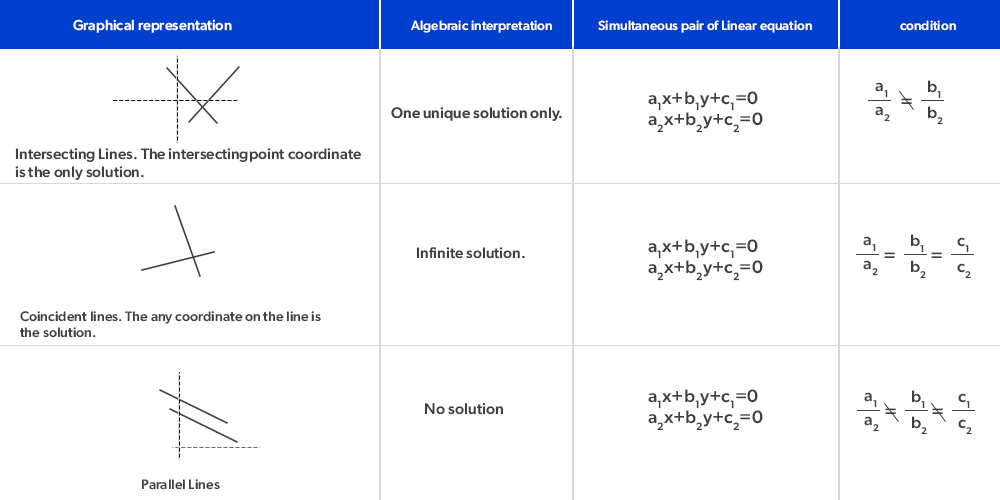
• Simultaneous Pair of Linear Equations: The pair of equations of the form:

a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0

• Graphically represented by two straight lines on the cartesian plane as discussed below:

第 4 章：二次方程

Quadratic equations are the polynomial equations of degree two in one variable of type: 

f(x) = ax² + bx + c 

where a, b, c, ∈ R and a ≠ 0. It is the general form of a quadratic equation where ‘a’ is called the leading coefficient and ‘c’ is called the absolute term of f (x). 

The values of x satisfying the quadratic equation are the roots of the quadratic equation (α,β). The quadratic equation will always have two roots. The nature of roots may be either real or imaginary. 

• Solution or roots of a quadratic equation are given by the quadratic formula:

(α, β) = [-b ± √(b2 – 4ac)]/2ac

• Roots of the quadratic equation: x = (-b ± √D)/2a, where D = b² – 4ac is known as the Discriminant of a quadratic equation. The discriminant of a quadratic equation decides the nature of roots.
• Nature of Roots of Quadratic Equation
  • D > 0, roots are real and distinct (unequal).
  • D = 0, roots are real and equal (coincident) i.e. α = β = -b/2a.
  • D < 0, roots are imaginary and unequal i.e α = (p + iq) and β = (p – iq). Where ‘iq’ is the imaginary part of a complex number.
• Sum of roots: S = α+β= -b/a = coefficient of x/coefficient of x²
• Product of roots: P = αβ = c/a = constant term/coefficient of x²
• Quadratic equation in the form of roots: x² – (α+β)x + (αβ) = 0
• The quadratic equations a₁x₂ + b₁x + c₁ = 0 and a₂x₂ + b₂x + c₂ = 0 have;
  • One common root if (b₁c₂ – b₂c₁)/(c₁a₂ – c₂a₁) = (c₁a₂ – c₂a₁)/(a₁b₂ – a₂b₁)
  • Both roots common if a₁/a₂ = b₁/b₂ = c₁/c₂
• In quadratic equation ax² + bx + c = 0 or [(x + b/2a)² – D/4a²]
  • If a > 0, minimum value = 4ac – b²/4a at x = -b/2a.
  • If a < 0, maximum value 4ac – b²/4a at x= -b/2a.
• If α, β, γ are roots of cubic equation ax³ + bx² + cx + d = 0, then, α + β + γ = -b/a, αβ + βγ + λα = c/a, and αβγ = -d/a

第 5 章：算术级数

我们日常生活中的许多事情都有其模式。序列是这些模式的名称。算术和几何序列是此类序列的两个示例。序列的项是出现在其中的各种数字。

• Arithmetic Progressions: a₁ a₂, a₃,………….. a_n are sequence terms. An arithmetic progression is a set of integers in which the difference between the terms is the same.
• Common difference: The difference between two consecutive term is the common difference of an AP. If a₁, a₂, a_3, a₄ a₅, a₆ are terms in an AP, then the common difference D = a₂– a₁ = a₃ – a₂ = …
• nth term of AP: a_n = a + (n – 1) d, where an is the nth term.
• Sum of nth terms of AP: S_n= n/2 [2a + (n – 1)d]

第 6 章：三角形

三角形是由三条直线靠近而成的三边闭合图形。在 CBSE Class 10 课程中，第 6 章主要讨论两个三角形之间的相似性标准和一些可能有助于理解三角形问题的重要定理。章节三角形总结的要点如下：

• Similar Triangles: The term is given to a pair of triangles that have equal corresponding angles and proportional corresponding sides.
• Equiangular Triangles: The term is given to a pair of triangles that have their corresponding angles equal, also the ratio of any two corresponding sides in two equiangular triangles is always the same.
• Criteria for Triangle Similarity
  1. Angle angle angle (AAA Similarity)
  2. Side angle Side (SAS) Similarity
  3. Side-side side (SSS) Similarity
• Basic Proportionality Theorem: According to this theorem, when a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, the other two sides are divided in the same ratio.
• Converse of Basic Proportionality Theorem: According to this theorem, in a pair of triangles when the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar.

第 7 章：坐标几何

坐标几何是数学的一部分，有助于在二维平面上表示几何形式并学习其属性。为了初步了解坐标几何，我们将了解坐标平面和点的坐标，如下文所述：

• Distance Formulae: For a line having two-point A(x₁, y₁) and B(x₂, y₂), then the distance of these points is given as:

AB= √[(x₂ − x₁)² + (y₂ − y₁)²]

• Section Formula: For any point p divides a line AB with coordinates A(x₁, y₁) and B(x₂, y₂), in ratio m:n, then the coordinates of the point p are given as:

P={[(mx₂ + nx₁) / (m + n)] , [(my₂ + ny₁) / (m + n)]}

• Midpoint Formula: The coordinates of the mid-point of a line AB with coordinates A(x₁, y₁) and B(x₂, y₂), are given as:

P = {(x₁ + x₂)/ 2, (y₁+y₂) / 2}

• Area of a Triangle: Consider the triangle formed by the points A(x₁, y₁) and B(x₂, y₂) and C(x₃, y₃) then the area of a triangle is given as-

∆ABC = ½ |x₁(y₂ − y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|

第 8 章：三角学简介

三角学是直角三角形的边和角之间关系的科学。三角比是直角三角形的边的比率。以下是一些与三角比相关的重要三角公式：

• If in a circle of radius r, an arc of length l subtends an angle of θ radians, then l = r × θ.
  • Radian Measure = π/180 × Degree Measure
  • Degree Measure = 180/π × Radian Measure
• Trigonometric ratios:
  • sin θ = (Perpendicular (P)) / (Hypotenuse (H)).
  • cos θ = (Base (B)) / ( Hypotenuse (H)).
  • tan θ = (Perpendicular (P)) / (Base (B)).
  • cosec θ = (Hypotenuse (H)) / (Perpendicular (P)).
  • sec θ = (Hypotenuse (H)) / (Base (B)).
  • cot θ = (Base (B)) / (Perpendicular (P)).
• Reciprocal Trigonometric Ratios:
  • sin θ = 1 / (cosec θ)
  • cosec θ = 1 / (sin θ)
  • cos θ = 1 / (sec θ)
  • sec θ = 1 / (cos θ)
  • tan θ =  1 / (cot θ)
  • cot θ = 1 / (tan θ)
• Trigonometric Ratios of Complementary Angles:
  • sin (90° – θ) = cos θ
  • cos (90° – θ) = sin θ
  • tan (90° – θ) = cot θ
  • cot (90° – θ) = tan θ
  • sec (90° – θ) = cosec θ
  • cosec (90° – θ) = sec θ
• Trigonometric Identities
  • sin² θ + cos² θ = 1 ⇒ sin² θ = 1 – cos² θ ⇒ cos² θ = 1 – sin² θ
  • cosec² θ – cot² θ = 1 ⇒ cosec² θ = 1 + cot² θ ⇒ cot² θ = cosec² θ – 1
  • sec² θ – tan² θ = 1 ⇒ sec² θ = 1 + tan² θ ⇒ tan² θ = sec² θ – 1

第 9 章：三角函数的一些应用

三角学可以在我们周围的事物中以多种方式使用，就像我们可以用它来计算某些物体的高度和距离，而无需实际计算它们。下面提到的是三角学的一些应用的章节摘要：

1. Line of Sight – The Line of Sight is the line formed by our vision as it passes through an item when we look at it.
2. Horizontal Line – The distance between the observer and the object is measured by a horizontal line.
3. Angle of Elevation – The angle formed by the line of sight to the top of the item and the horizontal line is called an angle of elevation. It is above the horizontal line, i.e. when we gaze up at the item, we make an angle of elevation.
4. Angle of Depression – When the spectator must look down to perceive the item, an angle of depression is formed. When the horizontal line is above the angle, the angle of depression is formed between it and the line of sight.

第 10 章：圆圈

圆是平面中与固定点保持恒定距离的所有点的集合。固定点称为圆心，距圆心的恒定距离称为半径。连接圆上任意两点的线段称为弦。通过圆心的弦称为直径。这是最长的和弦。当一条线在一点与圆相交时，这条线称为切线。圆的切线垂直于通过接触点的半径。

• The tangent to a circle equation x₂ + y₂ = a₂ for a line y = mx + c is given by the equation y = mx ± a √[1+ m₂].
• The tangent to a circle equation x₂ + y₂ = a₂ at (a₁,b₁) is xa₁ + yb₁ = a₂
• Circumference of the circle = 2 π r
• Area of the circle = π r²
• Area of the sector of angle, θ = (θ/360) × π r²
• Length of an arc of a sector of angle, θ = (θ/360) × 2 π r
• Distance moved by a wheel in one revolution = Circumference of the wheel.
• The number of revolutions = Total distance moved / Circumference of the wheel.

第 11 章：结构

构造有助于理解使用标尺和所需测量的罗盘为不同给定条件构造不同类型三角形的方法。这里提到了在第 10 课这一章中学到的重要结构列表，如下所示：

1. Determination of a Point Dividing a given Line Segment, Internally in the given Ratio M : N
2. Construction of a Tangent at a Point on a Circle to the Circle when its Centre is Known
3. Construction of a Tangent at a Point on a Circle to the Circle when its Centre is not Known
4. Construction of a Tangents from an External Point to a Circle when its Centre is Known
5. Construction of a Tangents from an External Point to a Circle when its Centre is not Known
6. Construction of a Triangle Similar to a given Triangle as per given Scale Factor m/n, m
7. Construction of a Triangle Similar to a given Triangle as per given Scale Factor m/n, m > n.

第 12 章：与圆相关的领域

面积、周长、线段、扇形、圆的角度和长度以及圆扇形的面积的基础知识都在这里涵盖。本节还包括几个平面和实体图形区域的可视化。下面提到的是与圆有关的领域的章节摘要中的要点，

• The equal chord of a circle is equidistant from the centre.
• The perpendicular drawn from the centre of a circle bisects the chord of the circle.
• The angle subtended at the centre by an arc = Double the angle at any part of the circumference of the circle.
• Angles subtended by the same arc in the same segment are equal.
• To a circle, if a tangent is drawn and a chord is drawn from the point of contact, then the angle made between the chord and the tangent is equal to the angle made in the alternate segment.
• The sum of the opposite angles of a cyclic quadrilateral is always 180°.
• Area of a Segment of a Circle: If AB is a chord that divides the circle into two parts, then the bigger part is known as the major segment and the smaller one is called the minor segment.

第 13 章：表面积和体积

本页解释了 Class 10 的表面积和体积的概念。本文将讨论立方体、长方体、圆锥体、圆柱体等几种固体形状的表面积和体积。横向表面积 (LSA)、总表面积 (TSA) 和曲面面积是表面积 (CSA) 的三种类型。让我们仔细看看各种三维几何形状的表面积和体积公式。本章可以检查几种实体形状的组合。此外，确定体积及其表面积的公式被提及为，

1. Total Surface Area (TSA): The whole area covered by the object’s surface is called the Total Surface area. Following is the list of the total surface areas of some important geometrical figures-
   1. TSA of a Cuboid = 2(l x b) +2(b x h) +2(h x l)
   2. TSA of a Cube = 6a²
   3. TSA of a Right circular Cylinder = 2πr(h+r)
   4. TSA of a Right circular Cone = πr(l+r)
   5. TSA of a Sphere = 4πr²
   6. TSA of a Right Pyramid = LSA + Area of the base
   7. TSA of a Prism = LSA × 2B
   8. TSA of a Hemisphere = 3 × π × r²
2. Lateral/Curved Surface Area: The curved surface area is the area of only the curved component, or in the case of cuboids or cubes, it is the area of only four sides, excluding the base and top. It’s called the lateral surface area for forms like cylinders and cones.
   1. CSA of a Cuboid = 2h(l+b)
   2. CSA of a Cube = 4a²
   3. CSA of a Right circular Cylinder = 2πrh
   4. CSA of a Right circular Cone = πrl
   5. LSA of a Right Pyramid = ½ × p × l
   6. LSA of a Prism = p × h
   7. LSA of a Hemisphere = 2 × π × r²

Volume: The volume of an object or material is the amount of space it takes up, measured in cubic units. There is no volume in a two-dimensional object, only area. A circle’s volume cannot be calculated since it is a 2D figure, while a sphere’s volume can be calculated because it is a 3D figure.

1. Volume of a Cuboid = l x b x h
2. Volume of a Cube = a³
3. Volume of a Right circular Cylinder = πr²h
4. Volume of a Right circular Cone = 1/3πr²h
5. Volume of a Sphere = 4/3πr³
6. Volume of a Right Pyramid = ⅓ × Area of the base × h
7. Volume of a Prism = B × h
8. Volume of a Hemisphere = ⅔ × (πr³)

Here, l is the length, b is the breadth, h is the height, r is the radius, a is the side, p is the perimeter of the base, B is the area of the base of the respective geometrical figure.

第 14 章：统计

第 10 类的统计主要包括对给定数据的研究 b 评估其平均值、众数、中位数。统计公式如下：

Mean

• Direct method: Mean, X = ∑f_i x_i / ∑f_i
• Assumed Mean Method: X = a + ∑f_i d_i / ∑f_i                                      (where d_i = x_i – a)
• Step Deviation Method: X = a + ∑f_i u_i / ∑f_i × h

Median is the middlemost term for an even number of observations while (n+1)th/2 observations for an odd number of observations.

Mode

$\text{Mode} = 1 + \left[\dfrac{f_1-f_0}{2f_1-f_0-f_2}\right]\times h$

where l is the lower limit of the modal class, f₁ is the frequency of the modal class, f₀ is the frequency of the preceding class of the modal class, f₂ is the frequency of the succeeding class of the modal class and h is the size of the class interval.

第15章：概率

概率表示某事发生的可能性。这是一个研究随机事件发生概率的数学领域。从 0 到 1，表示值。概率是一个数学概念，用于预测发生的概率。概率的定义是某事可能发生的程度。这是基本概率论，也适用于概率分布，您将在其中了解随机实验的可能结果。让我们讨论一下 10 年级课程中概率的一些重要公式：

Empirical Probability: The probability of events that depends on the experiments and it is defined as,

Empirical Probability = Number of Trials which expected outcome come / Total Number of Trials

Theoretical Probability: The probability of events that depends on the experiments and it is defined as,

Theoretical Probability = Number of favourable outcomes to E / Total Number of possible outcomes of the experiment