CBSE 8 级数学公式

GeeksforGeeks 挺身而出，以减轻学生在一个地方收集 8 级课程中使用的所有重要公式的压力。 GeeksforGeeks 的第 8 类数学公式的开发方式使其涵盖了每一章中使用的所有重要公式和属性，所有内容都很简短。这有助于学生轻松快速地复习和学习。对于一个 8 年级的学生来说，上一课的难度增加可能很难掌握。此外，对于像数学这样的学科，你必须时刻保持觉知。该主题在您的学校教育和您的个人生活中都非常重要。要获得高水平的知识，您必须先掌握第 8 课的数学公式，然后再将它们应用于您的问题。

您可能想知道在哪里可以获得特定问题集的第 8 类的确切数学公式。这就是 GeeksforGeeks 现在将这些信息呈现在您面前的原因。下面提到的是在一页上为您提供的第 8 类的所有数学公式，因此您不必寻找另一个！

第 1 章：有理数

在算术中，不同种类的数字包括整数、实数、自然数、整数、分数、素数和合数。 Rational Numbers Class 8 数学公式涵盖了不同类型的有理数，这将帮助学生学习有理数的概念、它们与其他数字的唯一性以及它们在高等算术中的用途。

任何可以表示为 a ⁄ b 其中 b ≠ 0 的数字都是有理数。以下是用于有理数的公式和性质：

• Additive Identity: (a ⁄ b + 0) = (a ⁄ b).
• Multiplicative Identity: (a ⁄ b) × 1 = (a/b).
• Multiplicative Inverse: (a ⁄ b) × (b/a) = 1.
• Additive Inverse: a + (-a) = (-a) + a = 0.
• Closure Property – Addition: For any two rational numbers a and b, a + b is also a rational number.
• Closure Property – Subtraction: For any two rational numbers a and b, a – b is also a rational number.
• Closure Property – Multiplication: For any two rational numbers a and b, a × b is also a rational number.
• Closure Property – Division: Rational numbers are not closed under division.
• Commutative Property – Addition: For any rational numbers a and b, a + b = b + a.
• Commutative Property – Subtraction: For any rational numbers a and b, a – b ≠ b – a.
• Commutative Property – Multiplication: For any rational numbers a and b, (a x b) = (b x a).
• Commutative Property – Division: For any rational numbers a and b, (a/b) ≠ (b/a).
• Associative Property – Addition: For any rational numbers a, b, and c, (a + b) + c = a + (b + c).
• Associative Property – Subtraction: For any rational numbers a, b, and c, (a – b) – c ≠ a – (b – c)
• Associative Property – Multiplication: For any rational number a, b, and c, (a x b) x c = a x (b x c).
• Associative Property – Division: For any rational numbers a, b, and c, (a / b) / c ≠ a / (b / c).
• Distributive Property: For any three rational numbers a, b and c, a × ( b + c ) = (a × b) +( a × c).

第 2 章：单变量线性方程组

一个变量的线性方程是一个表达式，表示为 ax+b = 0，其中 a 和 b 是任意两个整数，x 是一个变量，并且只包含一个解。顾名思义，一个变量的线性方程，这种类型的方程只有一个解。求解一个变量中的线性方程有四种不同的方法：

1. Linear equations of the type that has a Linear expression on one side and numbers on the other side:
   • Transpose the number to the side where all numbers are present, maintaining the sign of the number.
   • Solve (Add/subtract) the equation on both sides to get it as simpler as possible, to obtain the value of the variable.
2. Linear equations of the type that has variables on both sides:
   • Transpose both the number and the variable to get each on the same side maintaining the sign of the number.
   • Solve (Add/subtract) the equation on both sides to get it as simpler as possible, to obtain the value of the variable.
3. Linear equations of the type that has a number in the denominator and variables on both sides:
   • LCM of the denominator on both sides should be taken
   • Then multiply the LCM on both sides so that the equation is deduced to a simple form and then solve it like the Linear equations of the type that has variables on both sides to obtain the value of the variable.
4. Linear equations of the type that are Reducible to the Linear form:
   • Such equations are of the form: (x + a / x + b) = c / d.
   • Therefore, these equations are solved by the cross-multiplying numerator and denominator to get it into a simple linear form like (x + a) d = c (x + b). This is a Linear equation of the type that has variables on both sides which can be solved further to obtain the value of the variable.

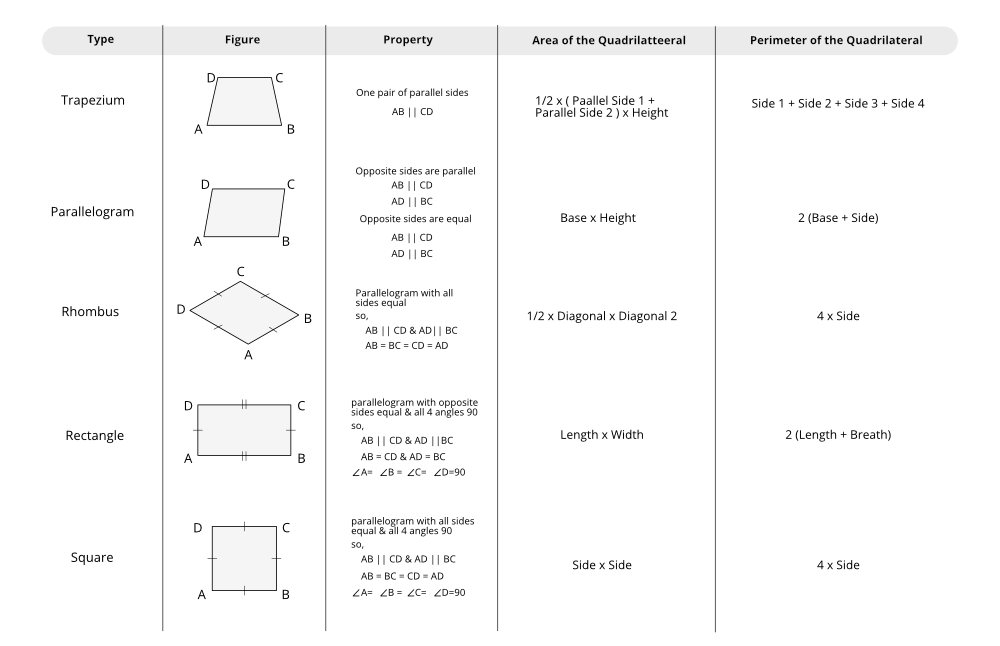
第 3 章：理解四边形

四边形是具有四个边、四个顶点和四个角的封闭对象，是一种多边形。它由连接在一起的四个非共线点组成。四边形的内角和总是 360 度。现在让我们了解有关本章讨论的公式的以下重要说明：

• Classification of Polygons: The polygons are classified according to the number of sides (or vertices) they have, as mentioned below:

• Angle Sum Property: This property states that the sum of all angles of a quadrilateral is 360°.
• Sum of the Measures of the Exterior Angles of a Polygon: Regardless of the number of sides in the polygons, the total of the measurements of the exterior angles equals 360 degrees.
• Types of Quadrilateral: The measurements of the angles and lengths of the sides of quadrilaterals are used to classify them. The total space occupied by the figure is the quadrilateral’s area. The perimeter of a two-dimensional form is the entire distance covered by its boundaries. The following are the properties, area, and perimeter equations for the various quadrilaterals:

第 4 章：实用几何

本章都是关于构造四边形的。四边形是一个几何图形，它是一个具有两条对角线的四边、四角多边形。例如正方形、长方形、菱形等。

To construct a quadrilateral uniquely, five measurements are required.  

• A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal are given.
• A quadrilateral can be constructed uniquely if its two diagonals and three sides are known.
• A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are known.
• A quadrilateral can be constructed uniquely if its three sides and two included angles are given.

第 5 章：数据处理

数据处理是指以对他人有帮助的方式收集、组织和呈现任何原始信息的过程，例如图形或图表等。我们需要研究的任何问题都需要收集数据，然后必须显示以这样一种方式，它提供了问题细节的清晰视觉表示，同时还检查了替代解决方案。以下是本章讨论的公式列表和重要术语：

• Data: Data is a systematic record of facts or distinct values of a quantity.
• Arranging data in an order to study their salient features is called the presentation of data.
• Frequency: It is defined as the number of times a particular entity occurs. A table is used to represent the frequency of different entities in the given data is termed a Frequency distribution table.
  • If the data present in the frequency distribution table is in the form of groups of the given values then it is called Grouped Frequency distribution table. This group data of the given values are grouped and called Class intervals. However, the number of values that each class contains is called the class size or width.
    1. The lower value in the class interval is called the Lower class limit.
    2. The upper value in the class interval is called the Upper-class limit.
• Graphical representation of data:
  1. Pictograph: Pictorial representation of data using symbols.
  2. Bar Graph: A display of information using bars of uniform width, their heights proportional to the respective values.
  3. Double Bar Graph: A bar graph showing two sets of data simultaneously. It is useful for the comparison of the data.
  4. Histogram: a graphical representation of frequency distribution in the form of rectangles with class intervals as bases and heights proportional to corresponding frequencies such that there is no gap between any successive rectangles.
  5. Circle Graph or Pie Chart: A pictorial representation of the numerical data in the form of sectors of a circle such that area of each sector is proportional to the magnitude of the data represented by the sector.
• Probability = Number of outcomes making up an event / Total number of outcomes, if the outcomes are equally likely.

第 6 章：平方和平方根

平方数是一个自然数 (Let q)，可以表示为 p ² ，其中 n 也是一个自然数。例如 4 是平方数，因为 4 = 2 ² 。平方根是平方的逆运算。

If q is a natural number such that p²= q then,

√q = p and –p

 Some of the important properties of Squares and Square roots are listed below:

• There are 2n non-perfect square numbers between n² and (n+1)².
• If a perfect square is of n digits then its square root will have n/2 digits if n is even, or (n+1)/2, if n is odd.

第 7 章：立方体和立方体根

立方公式的逆是立方根公式。我们在立方公式中将一个数乘以三次以获得它的立方，因此在这种情况下，我们将一个数分解为三个相等数的乘积并得到立方根。

Consider any number m, which can be expressed as the product of any number three times as m = n × n × n = n³. n³ is so known as the cube of n and m is now known as cube root of n:

³√m = n

Method of finding a Cube Root: There are two different ways to determine the cube root of a number, that are:

1. Prime Factorization Method
2. Estimation Method

第 8 章：比较数量

此处提供的第 8 类比较数量公式由专家精心准备，以帮助学生理解第 8 章中使用的所有概念和公式。下面提到的有关一些重要主题的公式，例如各种税，如销售税、增值税、商品和服务税、损益、百分比变化和折扣旨在帮助学生及时完成修改并获得更高的考试成绩。

The following formulas will help students understand the basics of simple arithmetic involving money as,

• Profit = Selling price – Cost price
• Loss = Cost price – Selling price
• If SP > CP , then it is profit.
• If SP = CP , then it is neither profit nor loss.
• If CP > SP , then it is loss.
• Discount = Marked Price – Sale Price
• Discount % = Discount × 100 / MP
• Profit Percentage = (Profit / Cost Price) × 100
• Loss Percentage = (Loss / Cost Price) × 100
• Percentage Increased = Change in Value / Original Value
• Simple Interest = (Principal × Rate × Time)/100
• Compound Interest Formula = Amount – Principal
• Sales tax or VAT =  Tax of  Selling price = (Cost Price × Rate of Sales Tax) / 100
• Billing Amount = Selling price + VAT

第 9 章：代数表达式和恒等式

第 8 课介绍代数表达式和代数恒等式，这是一个艰难的章节，您必须记住所有方程并正确应用它们。 GeeksforGeeks 通过将所有公式放在一页上，让他们变得简单。我们认为，这里提供了第 8 类的代数公式和代数恒等式。

These formulae will help students in learning fast and provide easy access to information when needed.

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b) (a – b) = a² – b²
• (x + a) (x + b) = x² + (a + b)x + ab
• (x + a) (x – b) = x² + (a – b)x – ab
• (x – a) (x + b) = x² + (b – a)x – ab
• (x – a) (x – b) = x² – (a + b)x + ab
• (a + b)3 = a³ + b³ + 3ab(a + b)
• (a – b)3 = a³ – b³ – 3ab(a – b)

第 10 章：可视化实体形状

立体几何在日常生活中至关重要，因为它可以帮助我们理解我们遇到的许多形式及其属性。对实体对象可视化的全面理解可以帮助学生掌握更复杂的几何原理并解决现实世界的情况。因此，了解与各种固体相关的众多公式至关重要，这将有助于日常计算。

Let’s learn about some important concepts and formulas used in this chapter

• Solids are defined by their form and the fact that they take up space. The faces of a solid are polygonal sections that make up the solid.
• Polyhedron: A polyhedron is a solid object bordered by polygons (platonic solid).
• Euler’s formula: A polyhedron has a certain number of planar faces, edges, and vertices that meet the formula:

F + V – E = 2

where F is the number of faces. The letters V and E stand for the number of vertices and edges, respectively.

• Prism: A prism is solid with parallelogram side faces and congruent parallel polygon ends (or bases). Two triangular faces, three rectangular faces, six vertices, and nine edges make up a prism.
• Pyramid: A pyramid is a polyhedron with a base that is a polygon with any number of sides and additional faces that are triangles with the same vertex. One square face, four triangular faces, five vertices, and eight edges make up a pyramid.
• Tetrahedron: If the base of a pyramid is a triangle, it is termed a triangular pyramid. The tetrahedron is another name for a triangular pyramid.
• Dimensions of a Solid: A solid item has three dimensions (measurements) – length, width, and height. Plane forms have two dimensions (measurements): length and breadth (or depth). As a result, they are referred to as two-dimensional and three-dimensional forms, respectively. They are referred to as two-dimensional and three-dimensional figures, respectively. Triangles, rectangles, and circles are two-dimensional forms, whereas cubes, cylinders, cones, and spheres are three-dimensional figures. From various angles, three-dimensional things appear to be different. As a result, they may be drawn from many angles, such as the top view, front view, and side view.
• Mapping: A map is not the same as a photograph. A map shows where one thing or place is in relation to other objects or locations. Symbols are used to represent various items and locations. On a map, there is no reference or perspective. Perspective, on the other hand, is critical when creating an image. Furthermore, maps have a scale that is set for each map.
• Faces, Vertices, and Edges: Faces are polygonal sections that make up a polyhedron. Edges are the line segments that connect the faces of a polyhedron. The vertices of a polyhedron are the spots where the edges cross. Three or more edges meet at a vertex of a polyhedron.

第11章：测量

此处列出了第 11 章第 8 类测量的公式。在这里，您将找到基于 CBSE 教学大纲（2021-2022）和最新考试模式的测量资源。通过公式和示例来更好地理解测量的概念。测量是计算各种几何形状（如三角形、梯形、矩形等）的面积和周长的过程。

• Perimeter: The length of the outline of any simple closed figure is known as the perimeter.
  • Perimeter of a rectangle = 2 × (l + b) units.
  • Perimeter of a square = 4 × side unit.
  • Perimeter of a circle is called its circumference. Therefore, the circumference of a circle is 2 π r.
  • Perimeter of a Parallelogram = 2(Base + Height)
  • Perimeter of a Triangle = a + b + c                                               (where a, b and c are the side lengths)
  • Perimeter of a Trapezium = a + b + c + d                                     (where a, b, c, d are the sides of a trapezoid)
  • Perimeter of a Kite =  2a + 2b                                                      (where a is the length of the first pair and b is the length of the second pair)
  • Perimeter of a Rhombus = 4 × side
  • Perimeter of a Hexagon = 6 × side
• Curved Surface Area of a Cone = 1 /2 × l × 2πr = πrl, where ‘r’ is its base radius and ‘l’ its slant height. ‘l’ = √(r² + h²)
• Volume of a Cuboid = Base Area × Height = Length × Breadth × Height
• Volume of a Cone = (1 / 3 )πr²h
• Volume of a Sphere = (4/3) π r³
• Volume of a Hemisphere = (2/3) πr³

第 12 章：指数和幂

指数表示值，它是指一个数字与其自身相乘的次数。例如，5 × 5 × 5 可以写成 5 ³ 。即使是非常小的数字也可以用负指数的形式表示。以下是与指数相关的一些定律的列表：

• Law of Product: a^m × aⁿ = a^{m + n}
• Law of Quotient: a^m/aⁿ = am – n
• Law of Zero Exponent: a⁰ = 1
• Law of Negative Exponent: a^-m = 1/a^m
• Law of Power of a Power: (a^m)n = a^mn
• Law of Power of a Product: (ab)ⁿ = a^mb^m
• Law of Power of a Quotient: (a/b)^m = a^m/b^m

第 13 章：正比和反比

为了表明数量和数量如何相互关联，使用了正比和反比。正比例和反比例是用于描述它们的其他术语。

• Proportions: The proportionality is represented by the symbol ∝. For example, if we claim that p is proportional to q, this implies p ∝ q and if we say that p is inversely proportional to q, then this implies “p∝1/q.” Some proportionality rules govern these relations. Now, the value of ‘p’ changes in terms of ‘q’ in both circumstances, or when the value of ‘q’ changes, the value of ‘p’ changes as well. A proportionality constant is equal to the change in both values. Essentially, a proportion indicates that two ratios, such as p/q and r/s, are equivalent, i.e., p/q = r/s.
• Direct Proportion or Variation: Any two quantities a and b can be said to be in direct proportion if they variate (increase or decrease) together with each other in such a way that the ratio of their corresponding values remains the same. This implies that, If a/b = k, where k is any positive number, then a and b are said to be in direct proportion. e.g. If the number of things bought increases, then the total cost of purchase also increases.
• Quantities that increase or decrease in parallel do not necessarily have to be in direct proportion, and inverse proportion does not always have to be in direct proportion.
• Inverse Proportion: Two quantities x and y are said to be in inverse proportion if an increase in x causes a proportional decrease in y (and vice-versa) in such a manner that the product of their corresponding values remains constant. That is, if xy = k, then x and y are said to vary inversely. e.g. If the number of people increases, the time taken to finish the food decreases. Or If the speed will increase the time required to cover a given distance will decrease.

第 14 章：因式分解

分解是将代数或二次方程简化为最简单形式的最常用方法之一。因此，需要熟悉因式分解公式才能分解复杂的方程。下面提到的是可用于解决多项式、三角学、代数和二次方程问题的各种公式和属性的列表。

• Factorisation: Factorization is the process of expressing an algebraic equation as a product of its components. Numbers, variables, or algebraic expressions can all be used as factors.
• Irreducible factor: A component that cannot be stated further as a product of factors is called irreducible.
• Method to do Factorisation: The common factor approach is a method for factoring an equation in a methodical way. There are three steps to solve it:
  • Each term of the statement should be written as a product of irreducible elements.
  • Look for and separate the components that are similar.
  • In each term, combine the remaining elements in line with the distributive law.
• All of the terms in a given expression may not share a common factor at times, but the terms can be grouped so that all of the terms in each group do. When we do this, a common factor emerges across all of the groups, resulting in the necessary factorization of the expression. This is the regrouping approach.
• When factoring by regrouping, keep in mind that any regrouping (i.e. rearrangement) of the terms in the provided equation may or may not result in factorization. We must observe the language and use trial and error to arrive at the desired regrouping.
• A number of factorable expressions are of the form or may be factored into the form: a² + 2ab + b², a² – 2ab + b², a² – b² and x² + (a + b)x + ab. These expressions can be easily factorized using below mentioned identities as,
  • a² + 2ab + b² = (a + b)²
  • a² – 2ab + b² = (a – b)²
  • a² – b² = (a + b) (a – b)
  • x² + (a + b)x + ab = (x + a)(x + b)
• Remember that the numerical term yields ab in formulations with factors of the kind (x + a) (x + b). Its factors, a and b, should be chosen in such a way that their sum, with signs taken into account, equals the x coefficient.
• When dividing a polynomial by a monomial, we can divide the polynomial either by dividing each term by the monomial or by using the common factor technique.
• We can’t divide each term in the dividend polynomial by the divisor polynomial when dividing a polynomial by another polynomial. Instead, both polynomials are factored and their common factors are cancelled.
• We have divisions of algebraic expressions in the case of divisions of algebraic expressions that we discussed in this chapter.

Dividend = Divisor × Quotient

or

Dividend = Divisor × Quotient + Remainder

第 15 章：图简介

使用图形工具显示数据对于组织和理解信息特别有效。以下是图形方法的一些示例：

• When comparing categories, the bar graph is the most appropriate tool.
• Pie charts are the best way to compare sections of a whole.
• A histogram may be used to make data simpler to interpret when it is presented in intervals.
• A line graph will be beneficial in the situation of data that changes constantly over time.
• The x-coordinate and y-coordinate are required to fix a point on the graph sheet.
• A graph depicts the relationship between a dependent variable and an independent variable.

第16章：玩数字

如果一个数字可以表示为它的数字及其相关位值的乘积之和，则称它为一般形式。数字可以用多种方式书写。因此，ab = 10a +b 将表示为两位数。在解决难题或玩数字游戏时，数字的一般形式很有用。当数字以一般形式表示时，可以提供被 10、5、2、9 或 3 整除的原因。

Rules for Divisibility:

• Divisibility by 2: A number is divisible by 2 when its one’s digit is 0, 2, 4, 6 or 8. e.g. 100a +10b +c here 100a and 10b are divisible by 2 because 100 and 10 are divisible by 2. Thus given number is divisible by 2 only when a = 0, 2, 4, 6 or 8.
• Divisibility by 3: A number is divisible by 3 when the sum of its digits is divisible by 3. e.g. 61785 the sum of digits = 6+1+7+8+5 = 27 which is divisible by 3. Therefore, 61785 is divisible 3.
• Divisibility by 4: A number is divisible by 4 when the number formed by its last two digits is divisible by 4. e.g.: 6216, 548, etc.
• Divisibility by 5: A number is divisible by 5 when its ones digit is 0 or 5. e.g.: 645, 540 etc.
• Divisibility by 6: A number is divisible by 6 when it is divisible by both 2 and 3. e.g.: 156, 5230, etc.
• Divisibility by 9: A number is divisible by 9 when the sum of its digits is divisible by 9. e.g.: consider a number 215847. Sum of digits = 2+1+5+8+4+7 = 27 which is divisible by 9. Therefore, 215847 is divisible by 9.
• Divisibility by 10: A number is divisible by 10 when its one digit is 0. e.g.: 540, 890, etc.
• Divisibility by 11: A number is divisible by 11 when the difference of the sum of its digits in odd places and the sum of its digits in even places is either o or a multiple of 11.