矩形电流回路上的转矩

扭矩是可以使物体绕轴扭转的力。力是导致物体在线性运动学中加速的原因。角加速度也是由扭矩引起的。因此，扭矩可以定义为线性力的旋转当量。项目旋转的点称为旋转轴。在物理学中，扭矩是力转动或扭曲的趋势。扭矩可以用多种方式表示，包括力矩和力矩。在这篇文章中，我们将研究如何在均匀磁场中计算载流矩形线环上的扭矩。

矩形电流回路上的转矩

Consider a rectangular loop that carries a current of magnitude I. When placed in a magnetic field, this loop experiences a torque but no net force, similar to what an electric dipole experiences in a homogeneous electric field. Consider the case where the rectangular loop is in the same plane as the magnetic field B. The loop’s arms that are parallel to the magnets receive no force from the field, but the arms that are perpendicular to the magnets receive a force equal to F₁.

F₁ = IbB

This force is directed in the plane’s direction. In the same way, we may write the formula for a force F₂ applied to the arm CD.

F₂ = IbB = F₁

The loop’s torque is given by, and the loop’s net force is zero.

τ = F₁(a/2) + F₂(a/2)

 = IbB(a/2) + IbB(a/2)

 = I(ab)B

τ = IAB

The area of the rectangle is ab. The loop rotates in an anti-clockwise manner due to the torque.

Consider the situation where the plane of the loop is not parallel to the magnetic field. Let be the angle generated by the field, and let be the coil’s normal is given by θ. The forces acting on the arms BC and DA will always be equal in size and will always act in opposite directions, as can be seen. The results of these forces cancel out because they are equal opposites and collinear at all points, resulting in zero-force or torque. The forces on the arms AB and CD are determined by F₁ and F₂. These forces are similar in size and direction and can be produced by,

F₁ = F₂ =  IbB

Because these forces are not collinear, the pair on the coil, causes a torque. The magnitude of the torque can be computed using,

τ = F₁(a/2) sin θ + F₂(a/2) sin θ

   = I(ab)B sin θ

τ = IAB sin θ

电流环转矩说明

当您对物体施加压力时，它会移动或施加一定的力。例如，从瓶子上旋下瓶盖、从包装上取下盖子、打开门把手、系鞋带等等。这是一种旋转运动，它是一种带有一些运动的扭矩运动。如果没有掌握扭矩的概念，就没有运动。扭矩是一个短语，指的是所有物品都具有的旋转运动，没有它我们将无法正常操作。

扭矩的公式是 τ = F × r，因为扭矩等于导致运动或旋转的扭转力。当根据旋转中心和施加力的位置之间的距离 (r) 向项目施加力 (f) 时，使用此公式。为了检测扭矩的方向，根据右手定则，学生应将右手手指向电流方向弯曲，拇指应伸出并指向区域矢量。

矢量形式的矩形电流回路方程上的转矩

考虑一个矩形线圈 PQRS 悬挂在具有均匀磁场的感应场 B 中。令 PQ = RS = l 和 QR = SP = b 为两个变量。令 I 表示沿 PQRS 方向流过线圈的电流，令 θ 为线圈平面与磁场方向形成的角度。这些力将作用在线圈的四个臂上。

The forces vector F₁ and vector F₃ acting on sides PQ and RS are equal and opposing, but their paths of action are distinct, according to Fleming’s left-hand rule; thus, the resultant force of vector F₁ and vector F₃ is zero, but they form a couple known as the deflecting couple. The perpendicular distance between vector F₁ and vector F₃ is bsinθ when the normal plane of the loop makes an angle with the direction of magnetic field B.

Since, Torque, τ = IAB sinθ 

So when the loop contains N-turns, then 

τ = NI ABsinθ 

In vector form,

$\vec τ = NI (\vec A \times \vec B)$

The direction of the torque is perpendicular to the direction of the area of the loop as well as the direction of the magnetic field i.e., along $(\vec A \times \vec B)$

结论

由于该扭矩，线圈沿其自身的轴旋转。它的值根据线圈平面和磁场方向形成的角度而变化。

• 如果电偶极子在电场中，则扭矩变为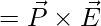， $\vec τ = \vec P \times \vec E$ ，其中，P 是电偶极矩，E 是电场。
• 如果磁偶极子处于磁场中，则扭矩变为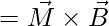， $\vec τ = \vec M \times \vec B$ ，其中，M 是磁偶极矩，B 是磁场。

Special cases

Case 1: If the coil is parallel with the magnetic field B direction,

Then, θ = 0^o and cos θ = 1. We have,

τ = nIBA cos θ 

= nIBA cos 0

= nIBA

∴ τ = nIBA (Maximum)

Case 2: If the coil is perpendicular with the magnetic field B direction,

Then, θ = 90^o and cos θ = 0.

τ = nIBA cos θ

= nIBA cos 90

= nIBA (0)

∴ τ = 0 (Minimum)

示例问题

问题 1：40 厘米宽的手柄在其边缘被 2N 的力释放时可以产生的最大扭矩是多少？

解决方案：

Given that: F = 2 N, 

d = 40 cm = 0.40 m 

τ = F × d

= 20 × 0.40

= 8 N-m

问题 2： 一个短棒形磁铁在 30 ^o的轴和 0.25 T 的均匀外部磁场下承受 4.5 × 10 ^-2 J 大小的扭矩。磁铁的磁矩有多大？

解决方案：

Given that: 

τ = 4.5 × 10^-2 J, 

θ = 30^o, 

B = 0.25 T

We have,

τ = MB sin θ 

4.5 × 10^-2 = M × 0.25 sin 30^o

∴ M = 0.36 J/T

问题 3：具有 2 × 10 ⁵ N/C 强度的电偶极子设置在 30 ^o角。它承受 4 Nm 的扭矩。偶极子上有 2 cm 的电荷。

解决方案：

Given that: 

E = 2 × 10⁵ N/C, 

τ = 4 Nm, 

l = 2 cm = 0.02 m

We have,

τ = pE sin θ 

4 = p × 2 × 10⁵ × sin θ

p = 4 × 10-5 Cm

q = p/l 

q = (4 × 10^-5)/0.02

q = 2 mC

问题4：在强度为0.8 Weber/m ²的均匀磁场中，垂直悬挂一个长0.56 m、宽0.2 m、绕40匝导线的矩形线圈。 6 A 的电流流过线圈。如果线圈平面与磁场方向成 90^度角，则保持线圈稳定平衡所需的扭矩为。

解决方案：

M = NIπr2

= 40 × 6 × 0.56 × 0.2

= 26.88

B = 0.8 T

We have,

τ = MB sin θ

= 26.88 × 0.8 sin 90^o

= 21.504 Nm

问题 5：如果一扇门的宽度为 80 厘米，并在其边缘被 2 N 的力释放，计算门产生的扭矩。

解决方案：

Given that:

F = 2 N, 

d = 80 cm = 0.80 m

τ = F × d

= 20 × 0.80

= 16 Nm 

问题 6：轴为 90 度的短条形磁铁，在^0.27 T 的均匀外部磁场下，会产生 2.51 × 10 ² J 的扭矩。磁铁的磁矩是多少？

解决方案：

Given that: 

τ = 2.51 × 10² J, 

θ = 90^o, 

B = 0.27 T

We have,

τ = MB sin θ

2.51 × 10² = M × 0.27 sin 90^o

M = 929  J/T

问题 7：获得在均匀磁场 B 中的矩形载流外观的转矩表达式。指出环路的转矩方向。

解决方案：

Consider a rectangular coil PQRS hanging in an induction field B with a uniform magnetic field. Let PQ = RS = l and QR = SP = b be the two variables. Let I represent the current flowing through the coil in the direction PQRS, and let θ be the angle formed by the coil’s plane with the magnetic field’s direction. The forces will act on the Coil’s four arms.

The forces vector F₁ and vector F₃ acting on sides PQ and RS are equal and opposing, but their paths of action are distinct, according to Fleming’s left-hand rule; thus, the resultant force of vector F₁ and vector F₃ is zero, but they form a couple known as the deflecting couple. The perpendicular distance between vector F₁ and vector F₃ is bsinθ when the normal plane of the loop makes an angle with the direction of magnetic field B.

Since, Torque, τ = IAB sinθ 

So when the loop contains N-turns, then 

τ = NI ABsinθ 

In vector form,

$\vec τ = NI (\vec A \times \vec B)$

The direction of the torque is perpendicular to the direction of the area of the loop as well as the direction of the magnetic field i.e., along $(\vec A \times \vec B)$