第 12 类 RD Sharma 解决方案 – 第 26 章标量三倍积 – 练习 26.1
问题 1(i)。评估以下内容![由 QuickLaTeX.com 渲染 [ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{j} ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_26_Scalar_Triple_Product_%E2%80%93_Exercise_26.1_0.jpg)
解决方案:
![]() =
= ![]()
=![]()
= 1 + 1 + 1
= 3
问题 1(ii)。评估以下内容![由 QuickLaTeX.com 渲染 [ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat{j} \ 2\hat{i} ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_26_Scalar_Triple_Product_%E2%80%93_Exercise_26.1_4.jpg)
解决方案:
![]() =
= ![]()
=![]()
= 2 – 1 – 2
= -1
问题 2(i)。找![由 QuickLaTeX.com 渲染 [ \bar{a}\ \bar{b}\ \bar{c} ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_26_Scalar_Triple_Product_%E2%80%93_Exercise_26.1_8.jpg) , 什么时候
, 什么时候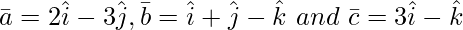
解决方案:
![]() =
= 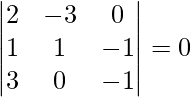
= 2(-1 – 0) + 3(-1 + 3)
= -2 + 6
= 4
问题 2(ii)。找![由 QuickLaTeX.com 渲染 [ \bar{a}\ \bar{b}\ \bar{c} ]](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_26_Scalar_Triple_Product_%E2%80%93_Exercise_26.1_12.jpg) , 什么时候
, 什么时候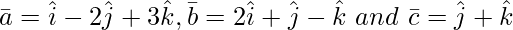
解决方案:
![]() =
= 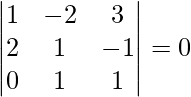
= 1(1 + 1) + 2(2 + 0) + 3(2 – 0)
= 2 + 4 + 6
= 12
问题 3(i)。求平行六面体的体积,其相邻边由向量表示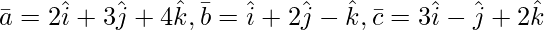
解决方案:
Volume of a parallelepiped whose adjacent edges are ![]() is equal to
is equal to ![]()
![]() =
= 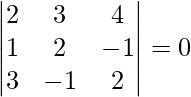
= 2(4 – 1) – 3(2 + 3) + 4(-1 – 6)
= 6 – 15 – 28
= -9 – 28
= -37
So, Volume of parallelepiped is | -37 | = 37 cubic unit.
问题 3(ii)。求平行六面体的体积,其相邻边由向量表示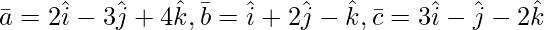
解决方案:
Volume of a parallelepiped whose adjacent edges ![]() are is equal to
are is equal to ![]()
![]() =
= 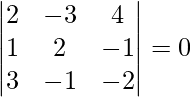
= 2(-4 – 1) + 3(-2 + 3) + 4(-1 – 6)
= -10 + 3 – 28
= -10 – 25
= -35
So, Volume of parallelepiped = | -35 | = 35 cubic unit.
问题 3(iii)。求平行六面体的体积,其相邻边由向量表示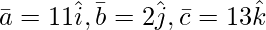
解决方案:
Let a = 11![]() , b = 2
, b = 2![]() , c = 13
, c = 13![]()
Volume of a parallelepiped whose adjacent edges are ![]() is equal to
is equal to ![]()
![]() =
= 
= 11(26 – 0) + 0 + 0
= 286
Volume of a parallelepiped = | 286| = 286 cubic units.
问题 3(iv)。求平行六面体的体积,其相邻边由向量表示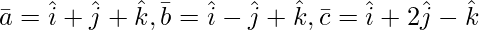
解决方案:
Let ![]()
Volume of a parallelepiped whose adjacent edges ![]() are is equal to
are is equal to ![]()
![]() =
=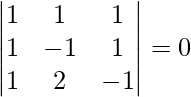
= 1(1 – 2) – 1(-1 – 1) + 1(2 + 1)
= -1 + 2 + 3
= 4
Volume of a parallelepiped = |4| = 4 cubic units.
问题 4(i)。下列三元组向量的显示是共面的: 
解决方案:
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 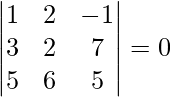
= 1(10 – 42) – 2(15 – 35) – 1(18 – 10)
= -32 + 40 – 8
= 0
So, the given vectors are coplanar.
问题 4(ii)。下列三元组向量的显示是共面的: 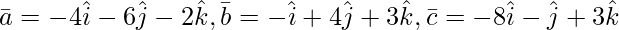
解决方案:
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 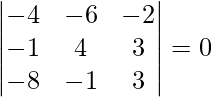
= -4(12 + 3) + 6(-3 + 24) – 2(1 + 32)
= -60 + 126 – 66
= 0
So, the given vectors are coplanar.
问题 4(iii)。下列三元组向量的显示是共面的: 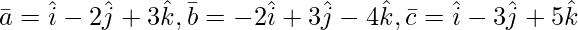
解决方案:
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 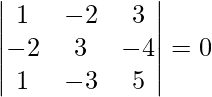
= 1(15 – 12) + 2(-10 + 4) + 3(6 – 3)
= 3 – 12 + 9
= 0
So, the given vectors are coplanar.
问题 5(i)。求 λ 的值,使以下向量共面: 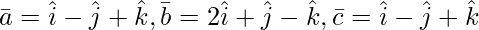
解决方案:
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 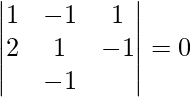
= 1(λ -1) + 1(2λ + λ) + 1(-2 – λ)
= λ – 1 + 3λ – 2 -λ
3 = 3λ
1 = λ
So, the value of λ is 1
问题 5(ii)。求 λ 的值,使以下向量共面: 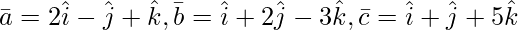
解决方案:
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 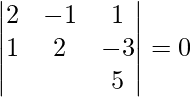
= 2(10 + 3 λ) + 1(5 + 3 λ) + 1(λ – 2 λ)
= 20 + 6 λ + 5 + 3 λ – λ
-25 = 8 λ
λ = – 25 / 8
So, the value of λ is -25/8
问题 5(iii)。求 λ 的值,使以下向量共面: 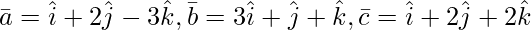
解决方案:
Given:
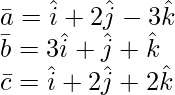
As we know that three vectors ![]() are coplanar if their
are coplanar if their ![]() = 0.
= 0.
![]() =
= 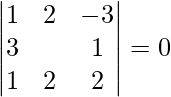
= 1(2λ – 2) – 2(6 – 1) – 3(6 – λ)
= 2λ – 2 -12 + 2 -18 + 3λ
= 5λ – 30
30 = 5λ
λ = 6
So, the value of the λ is 6
问题 5(iv)。求 λ 的值,使以下向量共面: 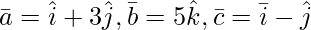
解决方案:
Given:
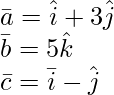
So, to prove that these points are coplanar, we have to prove that ![]() = 0
= 0
![]() =
= 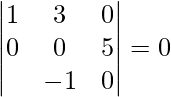
= 1(0 + 5) – 3(0 – 5λ) + 0
= 5 + 15λ
-5 = 15λ
λ = – 1 / 3
问题 6. 证明具有位置向量的四个点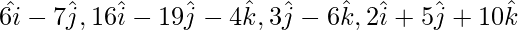 不共面。
不共面。
解决方案:
Let us considered
OA = ![]()
OB = ![]()
OC = ![]()
OD = ![]()
AB = OB – OA = ![]()
AC = OC – OA = ![]()
CD = OD – OC = ![]()
AD = OD – OA = ![]()
So, to prove that these points are coplanar, we have to prove that ![]()
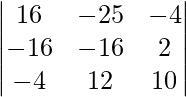
= 16(-160 – 24) + 25(-160 + 8) – 4(-144 + 64) ≠ 0
Hence, proved that the points are not coplanar.
问题 7. 证明点 A (-1, 4, -3), B(3, 2, -5), C(-3, 8, -5) 和 D(-3, 2, 1) 是共面
解决方案:
Given:
A = (-1, 4, -3)
B = (3, 2, -5)
C = (-3, 8, -5)
D = (-3, 2, 1)
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
So, to prove that these points are coplanar, we have to prove that ![]()
Thus, 
= 4[16 – 4] + 2[-8 -4] – 2[4 + 8]
= 48 – 24 – 24 = 0
Hence, proved.
问题 8. 证明四个点的位置向量是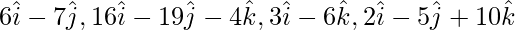
解决方案:
Let us considered
OA =![]()
OB = ![]()
OC = ![]()
OD =![]()
Thus,
AB = OB – OA = ![]()
AC = OC – OA = ![]()
AD = OD – OA = ![]()
If the vectors AB, AC and AD are coplanar then the four points are coplanar
On simplifying, we get
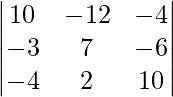
= 10(70 + 12) + 12(-30 – 24) – 4(-6 + 28)
= 820 – 648 – 88
= 84 ≠ 0
So, the points are not coplanar.
问题 9. 求具有位置向量的四个点的 λ 值 是共面的
是共面的
解决方案:
Let us considered:
Position vector of A = ![]()
Position vector of B = ![]()
Position vector of C = ![]()
Position vector of D = ![]()
If the given vectors ![]() are coplanar, then the four points are coplanar
are coplanar, then the four points are coplanar
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
On simplifying, we get
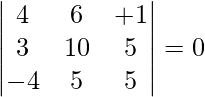
4(50 – 25) – 6(15 + 20) + (λ + 1)(15 + 40) = 0
100 – 210 + 55 + 55λ = 0
55λ = 55
λ = 1
So, when the value of λ = 1, the given points are coplanar.
问题 10. 证明![由 QuickLaTeX.com 渲染 ( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions_%E2%80%93_Chapter_26_Scalar_Triple_Product_%E2%80%93_Exercise_26.1_117.jpg)
解决方案:
Given: ![]()
One solving the given equation we get
=![]()
= ![]()
= 6 [ a b c ] – 6 [ a b c ]
= 0
Hence proved
问题 11。 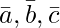 分别是点 A、B 和 C 的位置向量,证明
分别是点 A、B 和 C 的位置向量,证明 是垂直于三角形 ABC 平面的向量。
是垂直于三角形 ABC 平面的向量。
解决方案:
In the given triangle ABC,
If ![]() = AB
= AB
![]() = BC
= BC
![]() = AC
= AC
Then,
![]() is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
![]() is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
![]() is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
Hence, proved that ![]()
is a vector perpendicular to the plane of the given triangle ABC.
问题 12(i)。让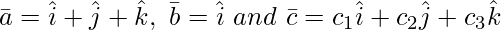 .然后,如果 c 1 = 1 和 c 2 = 2,找到 c 3使得
.然后,如果 c 1 = 1 和 c 2 = 2,找到 c 3使得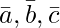 共面。
共面。
解决方案:
Given:
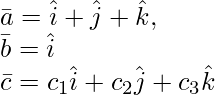
![]() are coplanar only if
are coplanar only if ![]() = 0
= 0
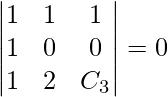
0 – 1(C3) + 1(2) = 0
C3 = 2
So, when the value C3 = 2, then these points are coplanar.
问题 12(ii)。让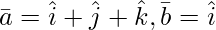 和
和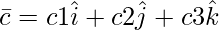 .然后,如果 c2 = -1 且 c3 =1,证明没有 c 1的值可以使
.然后,如果 c2 = -1 且 c3 =1,证明没有 c 1的值可以使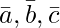 共面
共面
解决方案:
Given:
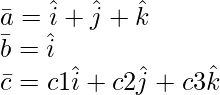
![]() are coplanar only if
are coplanar only if ![]() = 0
= 0
So,
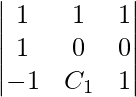
0 – 1 + 1 (C1) = 0
C1 = 1
Hence, prove that no value of C1 can make these points coplanar
问题 13. 求点 A (3, 2, 1)、B (4, λ, 5)、C (4, 2, -2) 和 D (6, 5, -1) 共面的 λ
解决方案:
Let us considered:
Position vector of OA = ![]()
Position vector of OB = ![]()
Position vector of OC = ![]()
Position vector of OD = ![]()
If the vectors AB, AC, and AD are coplanar, then the four points are coplanar
AB =![]()
AC =![]()
AD = ![]()
On simplifying, we get
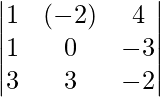
1(9) – (λ – 2)(-2 + 9) + 4(3 – 0) = 0
9 – 7 λ + 14 + 12 = 0
7 λ = 35
λ = 5
Hence, the value of λ is 5. So the coplanar points are, A(3, 2, 1), B(4, 5, 5), C(4, 2, -2), and D(6, 5, -1)