定积分的性质
有极限的积分称为定积分。它有上限和下限。它表示为
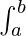 f(x) = F(b) - F(a)
f(x) = F(b) - F(a)
关于定积分有很多性质。我们还将用证据一一讨论每个属性。
特性
属性一: 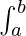 f(x) dx =
f(x) dx = 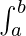 f(y) dy
f(y) dy
证明:
![]() f(x) dx…….(1)
f(x) dx…….(1)
Suppose x = y
dx = dy
Putting this in equation (1)
![]() f(y) dy
f(y) dy
属性 2: 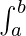 f(x) dx = –
f(x) dx = – ![由 QuickLaTeX.com 渲染 \int_{b}^{a}]() f(x) dx
f(x) dx
证明:
![]() f(x) dx = F(b) – F(a)……..(1)
f(x) dx = F(b) – F(a)……..(1)
![]() f(x) dx = F(a) – F(b)………. (2)
f(x) dx = F(a) – F(b)………. (2)
From (1) and (2)
We can derive ![]() f(x) dx = –
f(x) dx = – f(x) dx
属性 3: 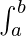 f(x) dx =
f(x) dx = 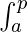 f(x) dx +
f(x) dx + 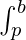 f(x) dx
f(x) dx
证明:
![]() f(x) dx = F(b) – F(a) ………..(1)
f(x) dx = F(b) – F(a) ………..(1)
![]() f(x) dx = F(p) – F(a) ………..(2)
f(x) dx = F(p) – F(a) ………..(2)
![]() f(x) dx = F(b) – F(p) ………..(3)
f(x) dx = F(b) – F(p) ………..(3)
From (2) and (3)
![]() f(x) dx +
f(x) dx +![]() f(x) dx = F(p) – F(a) + F(b) – F(p)
f(x) dx = F(p) – F(a) + F(b) – F(p)
![]() f(x) dx +
f(x) dx + ![]() f(x) dx = F(b) – F(a) =
f(x) dx = F(b) – F(a) = ![]() f(x) dx
f(x) dx
Hence, it is Proved.
属性 4.1: 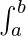 f(x) dx =
f(x) dx = 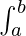 f(a + b – x) dx
f(a + b – x) dx
证明:
Suppose
a + b – x = y…………(1)
-dx = dy
From (1) you can see
when x = a
y = a + b – a
y = b
and when x = b
y = a + b – b
y = a
Replacing by these values he integration on right side becomes ![]() f(y)dy
f(y)dy
From property 1 and property 2 you can say that
![]() f(x) dx =
f(x) dx = ![]() f(a + b – x) dx
f(a + b – x) dx
属性 4.2:如果 a 的值为 0,则属性 4.1 可以写为
![]() f(x) dx =
f(x) dx = ![]() f(b – x) dx
f(b – x) dx
属性 5: 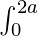 f(x) dx =
f(x) dx = 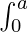 f(x) dx +
f(x) dx +  f(2a – x) dx
f(2a – x) dx
证明:
We can write ![]() f(x) dx as
f(x) dx as
![]() f(x) dx =
f(x) dx = ![]() f(x) dx +
f(x) dx + ![]() f(x) dx ………….. (1)
f(x) dx ………….. (1)
I = I1 + I2
(from property 3)
Suppose 2a – x = y
-dx = dy
Also when x = 0
y = 2a, and when x = a
y = 2a – a = a
So, ![]() f(2a – x)dx can be written as
f(2a – x)dx can be written as
![]() f(y) dy = I2
f(y) dy = I2
Replacing equation (1) with he value of I2 we get
![]() f(x) dx =
f(x) dx = ![]() f(x) dx +
f(x) dx + ![]() f(2a – x) dx
f(2a – x) dx
属性 6: 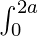 f(x) dx = 2
f(x) dx = 2 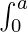 f(x) dx;如果 f(2a – x) = f(x)
f(x) dx;如果 f(2a – x) = f(x)
= 0;如果 f(2a – x) = -f(x)
证明:
From property 5 we can write ![]() f(x) dx as
f(x) dx as
![]() f(x) dx =
f(x) dx =![]() f(x) dx +
f(x) dx + ![]() f(2a – x) dx ………….(1)
f(2a – x) dx ………….(1)
Part 1: If f(2a – x) = f(x)
Then equation (1) can be written as
![]() f(x) dx =
f(x) dx =![]() f(x) dx +
f(x) dx + ![]() f(x) dx
f(x) dx
This can be further written as
![]() f(x) dx = 2
f(x) dx = 2 ![]() f(x) dx
f(x) dx
Part 2: If f(2a – x) = -f(x)
Then equation (1) can be written as
![]() f(x) dx=
f(x) dx=![]() f(x) dx –
f(x) dx – ![]() f(x) dx
f(x) dx
This can be further written as
![]() f(x) dx= 0
f(x) dx= 0
属性 7: 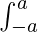 f(x) dx =
f(x) dx = 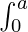 f(x) dx;如果一个函数是偶数,即 f(-x) = f(x)
f(x) dx;如果一个函数是偶数,即 f(-x) = f(x)
 = 0;如果一个函数是奇数,即 f(-x) = -f(x)
= 0;如果一个函数是奇数,即 f(-x) = -f(x)
证明:
From property 3 we can write
![]() f(x) dx as
f(x) dx as
![]() f(x) dx =
f(x) dx = ![]() f(x) dx +
f(x) dx + ![]() f(x) dx ………(1)
f(x) dx ………(1)
Suppose
![]() f(x) dx = I1 ……(2)
f(x) dx = I1 ……(2)
Now, assume x = -y
So, dx = -dy
And also when x = -a then
y= -(-a) = a
and when x = 0 then, y = 0
Putting these values in equation (2) we get
I1 = ![]() f(-y)dy
f(-y)dy
Using property 2, I1 can be written as
I1 = ![]() f(-y)dy
f(-y)dy
and using property 1 I1 can be written as
I1 = ![]() f(-x)dx
f(-x)dx
Putting value of I1 in equation (1), we get
![]() f(x) dx =
f(x) dx = ![]() f(-x) dx +
f(-x) dx +![]() f(x) dx ……….(3)
f(x) dx ……….(3)
Part 1: When f(-x) = f(x)
Then equation(3) becomes
![]() f(x) dx =
f(x) dx = ![]() f(x) dx +
f(x) dx + ![]() f(x) dx
f(x) dx
![]() f(x) dx = 2
f(x) dx = 2![]() f(x) dx
f(x) dx
Part 2: When f(-x) = -f(x)
Then equation 3 becomes
![]() f(x) dx = –
f(x) dx = –![]() f(x) dx +
f(x) dx +![]() f(x) d
f(x) d
![]() f(x)dx = 0
f(x)dx = 0
例子
示例1:我 = ![]() x(1 – x) 99分
x(1 – x) 99分
解决方案:
Using property 4.2 he given question can be written as
![]() (1 – x) [1 – (1 – x)]99 dx
(1 – x) [1 – (1 – x)]99 dx
![]() (1 – x) [1 – 1 + x]99 dx
(1 – x) [1 – 1 + x]99 dx
![]() (1 – x)x99 dx
(1 – x)x99 dx

= 1/100 – 1/101
= 1 / 10100
示例 2 :我 = ![]() cos(x) 日志
cos(x) 日志
解决方案:
f(x) = cos(x) log
f(-x) = cos(-x) log ![]()
f(-x) = -cos(x) log
f(-x) = -f(x)
Hence the function is odd. So, Using property
![]() f(x)dx = 0; if a function is odd i.e. f(-x) = -f(x)
f(x)dx = 0; if a function is odd i.e. f(-x) = -f(x)
![]() cos(x) log
cos(x) log ![]() = 0
= 0
示例 3:我 = ![]() [x] dx
[x] dx
解决方案:
![]() 0 dx +
0 dx + ![]() 1 dx +
1 dx + ![]() 2 dx +
2 dx +![]() 3 dx +
3 dx + ![]() 4 dx [using Property 3]
4 dx [using Property 3]
= 0 + [x]21 + 2[x]32 + 3[x]43 + 4[x]54
= 0 + (2 – 1) + 2(3 – 2) + 3(4 – 3) + 4(5 – 4)
= 0 + 1 + 2 + 3 + 4
= 10
示例 4:我 = ![]() |x| dx
|x| dx
解决方案:
![]() (-x) dx +
(-x) dx + ![]() (x) dx [using Property 3]
(x) dx [using Property 3]
= -[x2/2]0-1 + [x2/2]20
= -[0/2 – 1/2] + [4/2 – 0]
= 1/2 + 2
= 5/2