10类RD Sharma解决方案–第9章算术级数–练习9.6 |套装1

问题1.找到以下算术级数的总和：

(i)50、46、42…至10个学期

解决方案：

Given A.P. has first term(a) = 50, 

Common difference(d) = 46 – 50 = – 4 

and number of terms(n) = 10

So, Sum of A.P. = S₁₀ = n[2a + (n – 1)d] / 2

= 10[2(50) + (10 – 1)(-4)]/2

= (10)(100 – 36)/2 

= 320

Hence, the sum of the first 10 terms of A.P. is 320.

(ii)1、3、5、7…..至12个学期。

解决方案：

Given A.P. has first term(a) = 1, 

common difference(d) = 3 – 1 = 2 

and number of terms(n) = 12

So, Sum of A.P. = S₁₂ = n[2a + (n – 1)d] / 2

= 12[2(1) + (12 – 1)(2)]/2

= 12[2 + 22]/2 

= 144

Hence, the sum of the first 12 terms of A.P. is 144.

(iii)3、9 / 2、6、15 / 2，…至25个学期

解决方案：

Given A.P. has first term(a) = 3, 

Common difference(d) = 9/2 – 3 = 3/2 

and number of terms(n) = 25

So, Sum of A.P. = S₂₅ = n[2a + (n – 1)d] / 2

= 25[2(3) + (25 – 1)(3/2)]/2

= 25[6 + 36]/2 = 525

Hence, the sum of the first 25 terms of A.P. is 525.

(iv)41、36、31…..至12个学期。

解决方案：

Given A.P. has first term(a) = 41, 

Common difference(d) = 36 – 41 = -5 

and number of terms(n) = 12

So, Sum of A.P. = S₁₂ = n[2a + (n – 1)d] / 2

= 12[2(41) + (12 – 1)(-5)]/2

= 12[82 – 55] = 162

Hence, the sum of the first 12 terms of A.P. is 162.

(v)a + b，a – b，a – 3b，…..至22个词

解决方案：

Given A.P. has first term(a) = a + b, 

Common difference(d) = (a – b) – (a + b) = -2b 

and number of terms(n) = 22

So, Sum of A.P. = S₂₂ = n[2a + (n – 1)d] / 2

= 22[2(a + b) + (22 – 1)(-2b)]/2

= 11{2(a + b) – 22b)

= 11(2a – 40b) = 22a – 440b

Hence, the sum of the first 22 terms of A.P. is 22a – 440b.

(vi)(x – y) ² ，(x ² + y ² )，(x + y) ² ，…至n个项

解决方案：

Given A.P. has first term(a) = (x – y)², 

number of terms(n) = n and

Common difference(d) = x² + y² – (x – y)² = x² + y² – x² + y² + 2xy = 2xy

So, Sum of A.P. = S_n = n[2a + (n – 1)d] / 2

= n[2(x – y)²+(n – 1)(2xy)]/2

= n[(x – y)²+(n – 1)(xy)]

Hence, the sum of the first n terms of A.P. is n[(x – y)²+(n – 1)(xy)].

(vii) 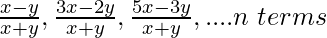$\frac{x-y}{x+y},\frac{3x-2y}{x+y},\frac{5x-3y}{x+y},....n\hspace{0.1cm}terms$

解决方案：

Given A.P. has first term(a) = $\frac{x-y}{x+y}$

number of terms(n) = n and

Common difference(d) = $\frac{3x-2y}{x+y}-\frac{x-y}{x+y}$        

= $\frac{2x-y}{x+y}$        

So, Sum of A.P. = S_n = n[2a + (n – 1)d] / 2

= $n\left[2\left(\frac{x-y}{x+y}\right) + (n-1) \left(\frac{2x-y}{x+y}\right)\right]/2$

= $\frac{n(2x-2y+2nx-ny-2x+y)}{2(x+y)}$

= $\frac{n[n(2x-y)]}{2(x+y)}$

Hence, the sum of the first n terms of A.P. is $\frac{n[n(2x-y)]}{2(x+y)}$

(viii)–26，–24，–22，…。至36个词

解决方案：

Given A.P. has first term(a) = -26, 

Common difference(d) = -24 – (-26) = 2 

and number of terms(n) = n.

So, Sum of A.P. = S₃₆ = n[2a + (n – 1)d] / 2

= 36[2(-26) + (36 – 1)2]/2

= 18[-52 + 70] = 324

Hence, the sum of the first 36 terms of A.P. is 324.

问题2.找到AP 5、2 – –1，– 4 – –7的n个项的总和。

解决方案：

Given A.P. has first term(a) = 5, 

Common difference(d) = 2 – 5 = -3

Sum of n terms of A.P. = S_n = n[2a + (n – 1)d] / 2

= n[2(5) + (n – 1)(-3)] / 2

= n{10 – 3n + 3)} / 2 

= n / 2(13 – 3n)

Hence, the sum of the n terms of A.P. is n/2(13 – 3n).

问题3.求出AP的n个项的总和，其项由_n = 5 – 6n给出。

解决方案：

Given A.P. has nth term, an = 5 – 6n

Putting n = 1, we get a, first term of the A.P.,

a = 5 – 6(1) = -1

Sum of n terms of A.P. = S_n = n[a + an]/2

= n[-1 + (5 – 6n)]/2

= n(4 – 6n)/2 = n(2 – 3n)

Hence, the sum of the n terms of A.P. is n(2 – 3n).

问题4.找出AP的最后十项之和：8、10、12、14，..，126。

解决方案：

Given A.P. has first term(a) = 8, 

Common difference(d) = 10 – 8 = 2 

and nth term(a_n) = 126.

The nth term of the A.P. is given by, a_n = a+(n – 1)d

=> 126 = 8 + (n – 1)(2)

=> 126 = 8 + 2n – 2

=> 2n = 120

=> n = 60

We have to find the sum of last ten terms i.e.,

S = a₅₁ + a₅₂ + a₅₃ + ……. + a₆₀

a₅₁ = 8 + (51 – 1)(2) = 8 + 50(2) = 108

So, sum would be S = 10[108 + 126]/2 = 5(234) = 1170

Hence, the sum of last 10 terms of the A.P. is 1170.

问题5.找到具有n个项的以下每个序列的前15个项的总和：

(i) _n = 3 + 4n

解决方案：

Given A.P. has nth term, a_n = 3 + 4n 

and number of terms(n) = 15

So, a_n = 3 + 4(15) = 63

On putting n = 1, we get a, first term of the A.P.,

a = 3 + 4(1) = 7

S₁₅ = n[a + a_n]/2

= 15(7 + 63)/2 = 15 x 35 = 525

Hence, the sum of the first 15 terms of given A.P. is 525.

(ii)b _n = 5 + 2n

解决方案：

Given A.P. has nth term, a_n = 5 + 2n and 

number of terms(n) = 15

So, a_n = 5 + 2(15) = 35

On putting n = 1, we get a, first term of the A.P.,

a = 5 + 2(1) = 7

S₁₅ = n[a + a_n]/2

= 15(7 + 35)/2 = 15 x 21 = 315

Hence, the sum of the first 15 terms of given A.P. is 315.

(iii)x _n = 6 – n

解决方案：

Given A.P. has nth term, a_n = 6 – n 

and number of terms(n) = 15

So, a_n = 6 – n = -9

On putting n = 1, we get a, first term of the A.P.,

a = 6 – 1 = 5

S₁₅ = n[a + a_n]/2

= 15(5 – 9)/2 = 15 x (-2) = -30

Hence, the sum of the first 15 terms of given A.P. is -30.

(iv)y _n = 9 – 5n

解决方案：

Given A.P. has nth term, a_n = 9 – 5n 

and number of terms(n) = 15

So, a_n = 9 – 5(15) = -66

On putting n = 1, we get a, first term of the A.P.,

a = 9 – 5 = 4

S₁₅ = n[a + a_n]/2

= 15(4 – 66)/2 = 15 x (-31) = -465

Hence, the sum of the first 15 terms of given A.P. is -465.

问题6.找出前20个项之和，即第n个项为_n = An + B的序列。

解决方案：

Given A.P. has nth term, a_n = An + B 

and number of terms(n) = 20

So, a_n = A(20) + B = 20A + B

On putting n = 1, we get a, first term of the A.P.,

a = A(1) + B = A + B

S₂₀ = n[a + a_n]/2

= 20(A+B + 20A + B)/2

= 10[21A + 2B]

= 210A + 20B

Hence, the sum of the first 20 terms of given A.P. is 210A + 20B.

_{问题7.求出第n个项由n} = 2 – 3n给出的AP的前25个项之和。

解决方案：

Given A.P. has nth term, a_n = 2 – 3n 

and number of terms(n) = 25

So, a_n = 2 – 3(25) = -73

On putting n = 1, we get a, first term of the A.P.,

a = 2 – 3(1) = -1

S₂₀ = n[a + a_n]/2

= 25(-1 – 73)/2

= 25 x (-37) = -925

Hence, the sum of the first 25 terms of given A.P. is -925.

_{问题8.求出第n个项由n} = 7 – 3n给出的AP的前25个项之和。

解决方案：

Given A.P. has nth term, a_n =  7 – 3n 

and number of terms(n) = 25

So, a_n = 7 – 3(25) = -68

On putting n = 1, we get a, first term of the A.P.,

a = 7 – 3(1) = 4

S₂₅ = n[a + a_n]/2

= 25(4 – 68)/2

= 25 x (-32)

= -800

Hence, the sum of the first 25 terms of given A.P. is -800.

问题9.如果从AP的第一项开始的一定数量的项的总和是25、22、19，…。 。 。是116。找到最后一项。

解决方案：

Given A.P. has first term(a) = 25, 

Common difference(d) = 22 – 25 = -3 and sum(S_n) = 116.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n – 1)d] / 2.

=> 116 = n[2(25) + (n − 1)(−3)]/2

=> n[53 − 3n]/2 = 116

=> 53n – 3n² = 232

=> 3n² – 53n + 232 = 0

=> 3n² – 24n – 29n + 232 = 0

=> 3n(n – 8) – 29 (n – 8) = 0

=> (3n – 29)( n – 8 ) = 0

=> n = 29/3 or n = 8

Ignoring n = 29/3 as number of terms cannot be a fraction, so we get, n = 8.

So, the last term is:

a₈ = a + (8 – 1)d = 25 + 7(-3) = 25 – 21 = 4

Hence, the last term of the given A.P. is 4.

问题10(i)。序列18、16、14…中有多少项。应该使它们的总和为零。

解决方案：

Given A.P. has first term(a) = 18, 

Common difference(d) = 16 – 18 = -2 and sum(S_n) = 0.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n – 1)d] / 2.

=> 0 = n[2(18) + (n – 1)(-2)]/2

=> 0 = n[36 + (-2n + 2)]/2

=> n[38 − 2n] = 0

=> n = 0 or 38 – 2n = 0

Ignoring n = 0 as number of terms cannot be 0. So we get,

=> 38 – 2n = 0

=> 2n = 38

=> n = 19

Hence, the number of terms(n) is 19.

(ii)在AP中有多少个术语，其第一和第五个术语分别为–14和2，且总和为40?

解决方案：

Given A.P. has first term(a) = –14, 

Fifth term(a₅) = 2 and sum(S_n) = 40.

Let the common difference of the A.P. be d. We get,

Then, a₅ = a + (5 – 1)d

=> 2 = -14 + 4d

=> 4d = 16

=> d = 4

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n – 1)d] / 2.

=> 40 = n[2(-14) + (n – 1)(4)]/2

=> 40 = n[-28 + (4n – 4)]/2

=> 40 = n[-32 + 4n]/2

=> 4n² – 32n – 80 = 0

=> n² – 8n – 20 = 0

=> n² -10n + 2n – 20 = 0

=> n(n -10) + 2(n – 10 ) = 0

=> (n + 2)(n – 10) = 0

=> n = -2 or n = 10

Ignoring n = -2 as number of terms cannot be negative. So we get, n = 10.

Hence, the number of terms (n) is 10.

( iii)AP 9、17、25，…中有多少条款。 。 。必须取为总和为636?

解决方案：

Given A.P. has first term(a) = 9, 

Common difference(d) = 17 – 9 = 8 and sum(S_n) = 636.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n – 1)d] / 2.

=> 636 = n[2(9) + (n − 1)(8)]/2

=> 636 = n[18 + (8n − 8)]/2

=>1271 = 10n + 8n²

=> 8n² + 10n − 1272 = 0

=> 4n²+ 5n − 636 = 0

=> 4n² − 48n + 53n − 636 = 0

=> 4n(n − 12) + 53(n − 12) = 0

=> (4n + 53)(n − 12) = 0

=> n = −53/4 or n = 12

Ignoring n = −53/4 as number of terms cannot be fraction. So we get, n = 12.

Hence, the number of terms (n) is 12.

(iv)AP 63、60、57，…的多少条款。 。 。必须取为总和为693?

解决方案：

Given A.P. has first term(a) = 63, 

Common difference(d) = 60 – 63 = -3 and sum(S_n) = 636.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n – 1)d] / 2.

=>  693 = n[2(63) + (n − 1)(−3)]/2

=> 693 = n[126+(−3n + 3)]/2

=> 693 = n[129 − 3n]/2

=> 129n − 3n² = 1386

=> 3n² − 129n + 1386 = 0

=> n² − 43n + 462 = 0

=> n² − 22n − 21n + 462 = 0

=> n(n − 22) − 21(n − 22) = 0

=> (n −22) (n −21) = 0

=> n = 22 or n = 21

So, the value of n can be both 21 as well as 22 because,

a₂₂ = a + 21d = 63 + 21(− 3) = 63 − 63 = 0

Sum remains the same even if we add the 22nd term because its value is 0.

Hence, the number of terms (n) is 21 or 22.

(v)AP的有效期为27、24、21。 。应该认为它们的和为零?

解决方案：

Given A.P. has first term(a) = 27, 

common difference(d) = 24 − 27 = −3 

and sum(S_n) = 0.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

=> 0 = n[2(27) + (n − 1)( − 3)]/2

=> 0 = n[54 + (n − 1)(-3)]

=> 0 = n[54 − 3n + 3]

=> n[57 − 3n] = 0

=> n = 0 or 3n = 57

Ignoring n = 0 as number of terms cannot be zero. So we get,

=> 3n = 57

=> n = 19

Hence, the number of terms (n) is 19.

问题11.求第一个的和

(i)AP的11个条款：2、6、10、14，…。 。 。

解决方案：

Given A.P. has first term(a) = 2, 

Common difference(d) = 6 − 2 = 4 

and number of terms(n) = 11.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₁₁ = 11[2(2) + (11 − 1)4]/2

= 11[4 + 40]/2

= 11 × 22 = 242

Hence, the sum of first 11 terms of the given A.P. is 242.

(ii)AP的13个条款：-6、0、6、12，…。 。 。

解决方案：

Given A.P. has first term(a) = -6, 

Common difference(d) = 0 − (−6) = 6 

and number of terms(n) = 13.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₁₃ = 13[2(−6) + (13 − 1)6]/2

= 13[(−12) + 72]/2

= 13[30] = 390

Hence, the sum of first 13 terms of the given A.P. is 390.

(iii)AP的51个任期：第二个任期为2，第四个任期为8。

解决方案：

Given A.P. has second term(a₂) = 2, 

Fourth term(a₄) = 8 and 

number of terms(n) = 51.

=> a₂ = a + d

=> 2 = a + d  …(1)

Also, a₄ = a + 3d

=> 8 = a + 3d  … (2)

Subtracting (1) from (2), we have

=> 2d = 6

=> d = 3

Putting d = 3 in (1), we get a = −1.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₅₁ = 51[2(−1) + (51 − 1)(3)]/2

= 51[−2 + 150]/2

= 51[74] = 3774

Hence, the sum of first 51 terms of the given A.P. is 3774.

问题12.求和

(i)8的前15倍

解决方案：

First 15 multiples of 8 are 8, 16, 24, …… , 120.

These multiples form an A.P. with first term(a) = 8, 

Common difference(d) = 16 − 8 = 8 

and number of terms(n) = 15.

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₁₅ = 15[2(8) + (15 − 1)8]/2

= 15[16 + 112]/2

= 15[64] = 960

Hence, the sum of the first 15 multiples of 8 is 960.

(ii)被(a)3(b)5(c)6整除的前40个正整数。

解决方案：

We know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

(a) First 40 positive integers divisible by 3 are 3, 6, 9, 12,…… ,120.

These integers form an A.P. with first term(a) = 3, 

Common difference(d) = 6 − 3 = 3 and number of terms(n) = 40.

S₄₀ = 40[2(3) + (40 − 1)3]/2

= 40(6 + 117)/2

= 20(123) = 2460

Hence, the sum of first 40 multiples of 3 is 2460.

(b) First 40 positive integers divisible by 5 are 5, 10, 15, 20,…… ,200.

These integers form an A.P. with first term(a) = 5, 

Common difference(d) = 10 − 5 = 5 and number of terms(n) = 40.

S₄₀ = 40[2(5) + (40 − 1)5]/2

= 40(10 + 195)/2

= 20(205) = 4100

Hence, the sum of first 40 multiples of 5 is 4100.

(c) First 40 positive integers divisible by 6 are 6, 12, 18, 24,…… ,240.

These integers form an A.P. with first term(a) = 6, 

Common difference(d) = 12 − 6 = 6 and number of terms(n) = 40.

S₄₀ = 40[2(6) + (40 − 1)6]/2

= 40(12 + 234)/2

= 20(246) = 4920

Hence, the sum of first 40 multiples of 6 is 4920.

(iii)所有可被13整除的3位数自然数。

解决方案：

All 3–digit natural numbers which are divisible by 13 are 104, 117,…… ,988.

These numbers form an A.P. with first term(a) = 104 and 

Common difference(d) = 117 − 104 = 13.

We know, the nth term of an A.P. id given by, a_n = a + (n − 1)d.

=> 988 = 104 + (n − 1)13

=> 988 = 104 + 13n -13

=> 988 = 91 + 13n

=> 13n = 897

=> n = 69

Also, we know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₆₉  = 69[2(104) + (69 − 1)13]/2

= 69[1092]/2

= 69(546) = 37674

Hence, the sum of all 3–digit natural numbers which are divisible by 13 is 37674.

(iv)所有3位数自然数，均为11的倍数。

解决方案：

All 3–digit natural numbers which are divisible by 11 are 110, 121, 132,…… ,990.

These numbers form an A.P. with first term(a) = 110 and 

Common difference(d) = 121 − 110 = 11.

We know, the nth term of an A.P. id given by, a_n = a + (n − 1)d.

=> 990 = 110 + (n − 1)11

=> 990 = 110 + 11n -11

=> 990 = 99 + 11n

=> 11n = 891

=> n = 81

Also, we know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₈₁ = 81[2(110) + (81 − 1)11]/2

= 81[1100]/2

= 81(550) = 44550

Hence, the sum of all 3–digit natural numbers which are divisible by 13 is 44550.

(v)所有2位数自然数可被4整除。

解决方案：

All 2-digit natural numbers divisible by 4 are 12, 16, 20,…… ,96.

These numbers form an A.P. with first term(a) = 4 

and common difference(d) = 16 − 12 = 4.

We know, the nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 96 = 12 + (n − 1)4

=> 4(n − 1) = 84

=>  n − 1 = 21

=> n = 22

Also, we know sum of n terms of an A.P. is given by, S_n = n[2a + (n − 1)d] / 2.

S₂₂ = 22[2(12) + (22 − 1)4]/2

= 22[24 + 84]/2

= 22[54] = 1188

Hence, the sum of all 2-digit natural numbers divisible by 4 is 1188.

问题13：求和：

(i)2 + 4 + 6 +。 。 。 + 200

解决方案：

Given series is an A.P. with first term(a) = 2, 

Common difference(d) = 4 − 2 = 2 and nth term(a_n) = 200.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 200 = 2 + (n − 1)2

=> 200 = 2 + 2n − 2

=> n = 200/2 

=> n = 100

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₁₀₀ = 100[2 + 200]/2

= 100[101] = 10100

Hence, the sum of terms of the given series is 10100.

(ii)3 + 11 + 19 +。 。 。 + 803

解决方案：

Given series is an A.P. with first term(a) = 3, 

Common difference(d) = 11 − 3 = 8 and nth term(a_n) = 803.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 803 = 3 + (n − 1)8

=> 803 = 3 + 8n − 8

=> n = 808/8 

=> n = 101

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₁₀₁ = 101[3 + 803]/2

= 101[403]

= 40703

Hence, the sum of terms of the given series is 40703.

(iii)(-5)+(-8)+(-11)+。 。 。 +(-230)

解决方案：

Given series is an A.P. with first term(a) = -5, 

Common difference(d) = (−8) − (−5) = −3 and nth term(a_n) = −230.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> −230 = −5 + (n − 1)(−3)

=> −230 = −5 − 3n + 3

=> n = 228/3

=> n = 76

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₇₆ = 76 [−5 + (−230)]/2

= 38 x (−235) = −8930

Hence, the sum of terms of the given series is –8930.

(iv)1 + 3 + 5 + 7 +。 。 。 + 199

解决方案：

Given series is an A.P. with first term(a) = 1,

Common difference(d) = 3 − 1 = 2 and nth term(a_n) = 199.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 199 = 1 + (n − 1)(2)

=> 199 = 1 + 2n − 2

=> n = 200/2 

=> n = 100

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₁₀₀ = 100[1 + 199]/2

= 50(200) = 10000

Hence, the sum of terms of the given series is 10000.

(ⅴ)7 + ^_10×1/2 + 14 +。 。 。 + 84

解决方案：

Given series is an A.P. with first term(a) = 7, 

Common difference(d) = 10¹/₂ − 7 = (21 − 14)/2 = 7/2 and nth term(a_n) = 84.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 84 = 7 + (n − 1)(7/2)

=> 168 = 14 + 7n − 7

=> n = 161/7 

=> n = 23

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₂₃ = 23[7 + 84]/2

= 23(91)/2

= 2093/2 = 1046.5

Hence, the sum of terms of the given series is 1046.5

(vi)34 + 32 + 30 +。 。 。 + 10

解决方案：

Given series is an A.P. with first term(a) = 34, 

Common difference(d) = 32 − 34 = −2 and nth term(a_n) = 10.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 10 = 34 + (n − 1)(−2)

=> 10 = 34 − 2n + 2

=> n = (36 −10)/2 

=> n = 13

Also, we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₁₃ = 13[34 + 10]/2

= 13(22)

= 286

Hence, the sum of terms of the given series is 286.

(vii)25 + 28 + 31 +。 。 。 + 100

解决方案：

Given series is an A.P. with first term(a) = 25, 

Common difference(d) = 28 − 25 = 3 and nth term(a_n) = 100.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 100 = 25 + (n − 1)(3)

=> 100 = 25 + 3n − 3

=> n = 88/3 

=> n = 26

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₂₆ = 26[25 + 100]/2

= 13(125)

= 1625

Hence, the sum of terms of the given series is 1625.

(ⅷ)18 + 15 ^_1/2 + 13 +。 。 。 +(-49^{_二分之一})

解决方案：

Given series is an A.P. with first term(a) = 18, 

Common difference(d) = $15\frac{1}{2}$ − 18 = (31 − 36)/2 = −5/2 and nth term(a_n) = $−49\frac{1}{2}$

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> $−49\frac{1}{2}$ = 18+(n − 1)(−5/2)

=> –135/2 = (n − 1)(−5/2)

=> n − 1 = 135/5

=> n = 28

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₂₈ = 28[18 + (−49¹/₂)]/2

= 14[−63/2]

= −441

Hence, the sum of terms of the given series is −441.

问题14. AP的第一项和最后一项分别为17和350。如果共同的差异是9，那么有多少个术语，它们的总和是多少?

解决方案：

Given A.P. has first term(a) = 17, 

Common difference(d) = 9 and last term(a_n) = 350.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d.

=> 350 = 17 + (n − 1) 9

=> 350 = 17 + 9n − 9

=> 9n = 342

=> n = 38

Also we know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

S₃₈ = 38(17 + 350)/2

= 19(367) = 6973

Hence, the number of terms of the given A.P is 38 and sum is 6973.

问题15. AP的第三项为7，第七项超过第三项的三倍，即为2。求出第一项，共同差和前20个项之和。

解决方案：

Given A.P. has third term(a₃) = 7 and seventh term(a₇) = 3a₃ + 2 = 3(7) + 2 = 23.

We know nth term of an A.P. is given by, a_n = a + (n − 1)d. So, we get,

a + 2d = 7 ….. (1)

a + 6d = 23 ….. (2)

Subtracting (1) from (2), we get,

=> (a + 6d) − (a + 2d) = 23 − 7

=> 4d = 16

=> d = 4

On putting d = 4 in (1), we get,

=> a + 2(4) = 7

=> a = 7 − 8

=> a = −1

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d] / 2.

Here a = −1, d = −4, n = 20. So sum is,

S₂₀ = 20[2(−1) + (20 − 1)(4)]/2

= 20[-2 + 76]/2

= 20[39] = 740

Hence, the sum of first 20 terms for the given A.P. is 740.

问题16. AP的第一项是2，最后一项是50。所有这些项的总和是442。找到共同的区别。

解决方案：

Given A.P. has first term(a) = 2, last term(a_n) = 50 and sum(S_n) = 442.

We know sum of n terms of an A.P. is given by S_n = n[a + a_n]/2.

=> 442 = n[2 + 50]/2

=> 26n = 442

=> n = 17

Also, we know nth term of an A.P. is given by, a_n = a + (n − 1)d. So, we get,

=> 50 = 2 + (17 − 1)d

=> 16d = 48

=> d = 3

Hence, the common difference of the A.P. is 3.

问题17.如果AP的第12个学期是–13，而前四个学期的总和是24，那么前10个学期的总和是多少?

解决方案：

We are given,

12th term of the A.P., (a₁₂) = a + 11d = −13  …. (1)

Sum of first four terms = S₄  = 4[2a + (4 − 1)d]/2 = 24  

=> 24 = 4[2a + 3d]/2

=> 2a + 3d = 12  ….. (2)

On multiplying eq(1) by 2 and subtracting eq(2) from it we get,

=> (2a+3d) − 2(a+11d) = 12 − 2(−13)

=> 2a + 3d − 2a − 22d = 38

=> −19d = 38

=> d = −2

On putting the value of d in eq(1), we get,

=> a + 11(−2) = −13

=> a = −13 + 22

=> a = 9

Now, sum of first 10 terms is given by,

S₁₀ = 10[2(9) + (10 − 1)(−2)]/2

= 10(18 − 18)/2 = 0

Hence, the sum of first 10 terms of the given A.P. is 0.

问题18：求该序列的n个项的总和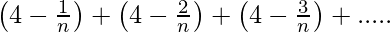$\left(4-\frac{1}{n}\right)+\left(4-\frac{2}{n}\right)+\left(4-\frac{3}{n}\right)+.....$

解决方案：

Given A.P. has first term(a) = $4-\frac{1}{n}$ 

Common difference(d) = $\left(4-\frac{2}{n}\right)-\left(4-\frac{1}{n}\right)$

= $\frac{4n-2-4n+1}{n}$ 

= -1/n 

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d] / 2

= $\frac{n}{2}\left[2\left(4-\frac{2}{n}\right)+(n-1)\left(\frac{-1}{n}\right)\right]$

= $\frac{n}{2}\left[8-\frac{2}{n}-1+\frac{1}{n}\right]$

= $\frac{n}{2}\left[\frac{8n-2-n+1}{n}\right]$

= $\frac{7n-1}{2}$

Hence, the sum of n terms of the given A.P. is $\frac{7n-1}{2}$

问题19。在AP中，如果第一项为22，则公共差为–4，n个项的和为64，则找到n。

解决方案：

Given A.P. has first term(a) = 22, common difference(d) = −4 and sum(S_n) = 64.

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d] / 2.

=> 64 = n[2(22) + (n − 1)(−4)]/2

=> 64 = n[44 − 4n + 4]/2

=> 48n − 4n² =128 

=> 4n² − 48n + 128 = 0

=> n² − 12n + 32 = 0

=> n² − 8n − 4n + 32 = 0

=> n(n − 8) − 4(n − 8) = 0

=> (n − 8)(n − 4) = 0

=> n = 8 or n = 4

Hence, the number of terms are either 4 or 8.

问题20.在AP中，如果第5和第12项分别是30和65，那么前20个项之和是多少?

解决方案：

Given A.P. has,

Fifth term, a₅ = a + 4d = 30  …..(1)

Twelfth term, a₁₂ = a + 11d = 65  ….(2)

On subtracting eq(1) from (2), we get,

=> (a + 11d) − (a + 4d) = 65 − 30

=> 7d = 35

=> d = 5

On putting d = 5 in eq(1), we get,

=> a + 4(5) = 30

=> a = 30 − 20

=> a = 10

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d] / 2.

Here a = 10, d = 5 and n = 20. So we get,

S₂₀ = 20[2(10) + (20 − 1)(5)]/2

= 20[20 + 95]/2

= 10[115] = 1150

Hence, the sum of first 20 terms for the given A.P. is 1150.

问题21.找到第二项和第三项分别为14和18的AP的前51个项之和。

解决方案：

Given A.P. has,

Second term, a₂ = a + d = 14  …..(1)

Third term, a₃ = a + 2d = 18

Hence, common difference(d) = a₃ − a₂ = 18 − 14 = 4.

On putting d = 4 in (1), we get,

=> a + 4 = 14

=> a = 10

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d] / 2.

Here a = 10, d = 4 and n = 51. So we get,

S₅₁ = 51[2(10) + (51 − 1)(4)]/2

= 51[20 + 200]/2

= 51[110] = 5610

Hence, the sum of first 51 terms for the given A.P. is 5610.

问题22.如果一个AP的7个项的总和为49，而17个项的总和为289，则找到n个项的总和。

解决方案：

We know sum of n terms of an A.P. is given by S_n = n[2a + (n − 1)d]/2. 

So we get, S₇ = 49

=> 7[2a + (7 − 1)d]/2 = 49

=> 7[a + 3d] = 49

=> a + 3d = 7 ….. (1)

And also, S₁₇ = 289

=> 17[2a + (17 − 1)d]/2 = 289

=> 17[a + 8d] = 289

=> a + 8d = 17 ….. (2)

On subtracting eq(1) from (2), we get,

=> a + 8d − (a + 3d) = 17 − 7

=> 5d = 10

=> d = 2

On putting d = 2 in (1), we get,

=> a + 3(2) = 7

=> a = 1

Here a = 1, d = 2, so sum of n terms would be,

S_n = n[2(1) + (n − 1)(2)]/2

= n[2 + 2n − 2]/2

= n[n] = n²

Hence, the sum of n terms of the given A.P is n².

问题23. AP的第一项为5，最后一项为45，总和为400。找到项数和共同差异。

解决方案：

Given A.P. has first term(a) = 5, last term(a_n) = 45 and sum(S_n) = 400.

We know sum of n terms of an A.P. is given by, S_n = n[a + a_n]/2

=> 400 = n[5 + 45]/2

=> 50n = 800

=> n = 16

Also, we know nth term of an A.P. given by, a_n = a + (n − 1)d.

=> 45 = 5 + (16 − 1)d

=> 15d = 40

=> d = 8/3

Hence, the number of terms of given A.P. is 16 and common difference is 8/3.

问题24.在AP中，第一个项是8，第n个项是33，前n个项的总和是123。求n和d是共同的区别。

解决方案：

Given A.P. has first term(a) = 8, nth term(a_n) = 33 and sum(S_n) = 123.

We know sum of n terms of an A.P. is given by, S_n = n[a + a_n]/2

=> 123 = n[8 + 33]/2

=> 41n = 246

=> n = 6

Also, we know nth term of an A.P. given by, a_n = a + (n − 1)d.

=> 33 = 8 + (6 − 1)d

=> 5d = 25

=> d = 5

Hence, the number of terms of given A.P. is 6 and common difference is 5.