10级RD Sharma解决方案–第4章三角形–练习4.3

问题1：在∆ABC中，AD是∠A的等分线，在D处遇到BC侧。

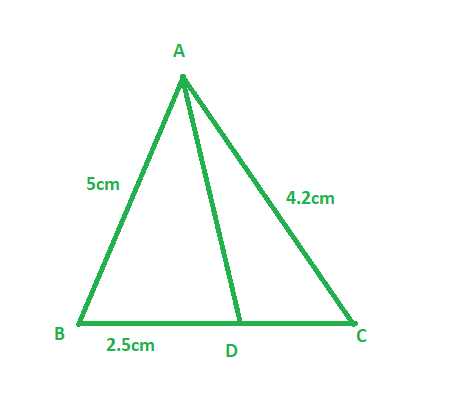
(i)如果BD = 2.5厘米，AB = 5厘米，AC = 4.2厘米，请找到DC

解决方案：

Given:

Length of side BD = 2.5 cm, AB = 5 cm, and AC = 4.2 cm.

To find: Length of side DC

In Δ ABC, AD is the bisector of ∠A, meeting side BC at D.

Since, AD is ∠A bisector,

Therefore, 

AB/AC = 2.5/DC

5/4.2 = 2.5/DC                 ( Since, AB = 5 cm, and AC = 4.2 cm )

5DC = 4.2 × 2.5

DC = (4.2 × 2.5)/5

DC = 2.1cm

Therefore, Length of side DC is 2.1 cm

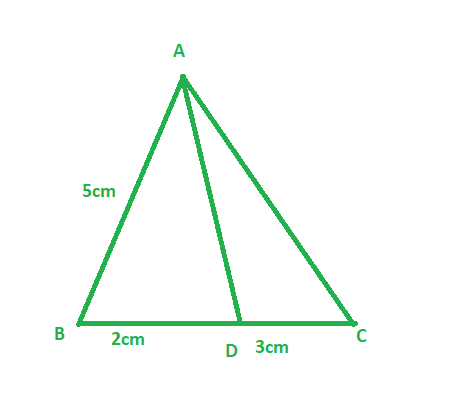
(ii)如果BD = 2厘米，AB = 5厘米，DC = 3厘米，找到AC

解决方案：

Given:

Length of side BD = 2 cm, AB = 5 cm, and DC = 3 cm

To find: Length of side AC

In Δ ABC, AD is the bisector of ∠A, meeting side BC at D

Since, AD is ∠A bisector.

Therefore,

AB/AC = BD/DC                                                (since AD is the bisector of ∠A and side BC)

5/ AC = 2/3                                                     (Since, BD = 2 cm, AB = 5 cm, and DC = 3 cm )

2AC = 5 × 3

AC = 15/2

AC = 7.5 cm

Therefore ,Length of side AC is 7.5 cm

(iii)如果AB = 3.5厘米，AC = 4.2厘米，DC = 2.8厘米，找到BD

解决方案：

Given:

Length of side AB = 3.5 cm, AC = 4.2 cm, and DC = 2.8 cm

To find: Length of side BD

In Δ ABC, AD is the bisector of ∠A, meeting side BC at D

Since, AD is ∠A bisector

Therefore,

⇒ AB/ AC = BD/ DC

3.5/ 4.2 = BD/ 2.8                       (Since, AB = 3.5 cm, AC = 4.2 cm, and DC = 2.8 cm)

4.2 x BD = 3.5 × 2.8

BD = 7/3

∴ BD = 2.3 cm

Therefore, Length of side BD is 2.3 cm

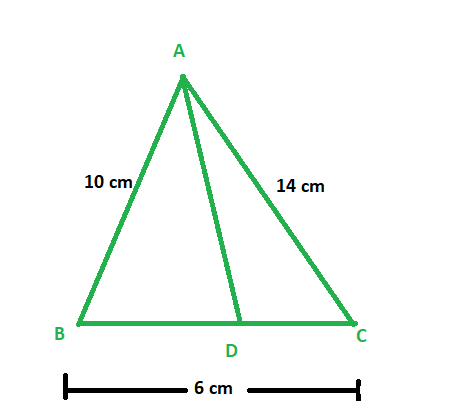
(iv)如果AB = 10厘米，AC = 14厘米，BC = 6厘米，找到BD和DC。

解决方案：

Given: 

 Length of side AB = 10 cm, AC = 14 cm, and BC = 6 cm

To find: Length of side BD and DC

In Δ ABC, AD is the bisector of ∠A meeting side BC at D

Since, AD is bisector of ∠A

Therefore, 

AB/AC = BD/DC                    – equation 1

Let BD be x, then DC = 6-x

Now, putting values in equation 1

⇒10/ 14 = x/ (6 – x)        

14x = 60 – 6x

20x = 60

x = 60/20

∴ BD = 3 cm and DC = (6 – 3) = 3 cm.

Therefore, Length of side BD is 3 cm and DC is 3cm

(v)如果AC = 4.2厘米，DC = 6厘米，BC = 10厘米，找到AB

解决方案：

Given:

 Length of side AC = 4.2 cm, DC = 6 cm, and BC = 10 cm.

To find: Length of side AB

In Δ ABC, AD is the bisector of ∠A, meeting side BC at D.

Since, AD is the bisector of ∠A

Therefore, we get

⇒ AB/ AC = BD/ DC

AB/ 4.2 = BD/ 6

We know that,

BD = BC – DC = 10 – 6 = 4 cm

⇒ AB/ 4.2 = 4/ 6

AB = (2 × 4.2)/ 3

∴ AB = 2.8 cm

Therefore, Length of side AB is 2.8 cm

(vi)如果AB = 5.6厘米，AC = 6厘米，DC = 3厘米，求BC

解决方案：

Given:

  Length of side AB = 5.6 cm, BC = 6 cm, and DC = 3 cm

To find: Length of side BC

In Δ ABC, AD is the bisector of  ∠A,  meeting side BC at D

Since, AD is the ∠A bisector

Therefore, we get

⇒ AB/ AC = BD/ DC

5.6/ 6 = BD/ 3

BD = 5.6/ 2 = 2.8cm

And, we know that,

BD = BC – DC

2.8 = BC – 3

2.8 + 3 = BC

∴ BC = 5.8 cm

Therefore, Length of side BC is 5.8 cm

(vii)如果AD = 5.6厘米，BC = 6厘米，BD = 3.2厘米，找到AC

解决方案：

Given:

Length of side AB = 5.6 cm, BC = 6 cm, and BD = 3.2 cm

To find: Length of side AC

In Δ ABC, AD is the bisector of ∠A, meeting side BC at D

Therefore, we get

⇒ AB/ AC = BD/ DC

5.6/ AC = 3.2/ DC

And, we know that

BD = BC – DC

3.2 = 6 – DC

∴ DC = 2.8 cm

⇒ 5.6/ AC = 3.2/ 2.8

AC = (5.6 × 2.8)/ 3.2

∴ AC = 4.9 cm

Therefore, Length of side AC is 4.9 cm

(viii)如果AB = 10厘米，AC = 6厘米，BC = 12厘米，找到BD和DC

解决方案：

Given:

Length of side AB = 10 cm, AC = 6 cm, and BC = 12 cm

To find: Length of side BD and DC

In Δ ABC, AD is the ∠A bisector, meeting side BC at D.

Since, AD is bisector of ∠A

Therefore, we get

⇒ AB/ AC = BD/ DC

10/ 6 = BD/ DC                                 – equation 1

And, we also know that

BD = BC – DC = 12 – DC

Let  length of side BD be x,

Then length of side DC will be 12 – x

Now putting values in equation 1, we get

10/ 6 = x/ (12 – x)

5(12 – x) = 3x

60 -5x = 3x

∴ x = 60/8 = 7.5

Hence, DC = 12 – 7.5 = 4.5cm and BD = 7.5 cm

Therefore ,Length of side BD is 7.5 cm and DC is 4.5 cm

问题2：在图中，AE是在E中产生的满足BC的外部∠CAD的等分线。如果AB = 10 cm，AC = 6 cm，BC = 12 cm，则找到CE。

解决方案：

Given:

Length of side AB = 10 cm, AC = 6 cm and BC = 12 cm

And, AE is the bisector of the exterior ∠CAD

To find: Length of side CE

Since, AE is the bisector of the exterior ∠CAD

Therefore, we get,

BE / CE = AB / AC ‘                               – equation 1

Let length of side CE be x

Therefore, BE = 12+ x

Now, putting this value in equation 1

(12+x)/ x = 10/ 6

6x + 72 = 10x

10x – 6x = 72

4x = 72

∴ x = 18

Since CE = x 

Therefore, Length of side CE is 18 cm

问题3： ΔABC是一个三角形，使得AB / AC = BD / DC，∠B= 70 ^o ，∠C= 50 ^o ，找到，BAD。

解决方案：

Given: 

Δ ABC such that AB/AC = BD/DC, ∠B = 70^o and ∠C = 50^o

To find: ∠BAD

In Δ ABC,

∠A + ∠B + ∠C = 180⁰

∠A = 180⁰ – (70^o + 50^o)

= 180^o – 120^o

= 60^o

Since, AB/AC = BD/DC

Therefore, AD is the bisector of ∠A

Therefore, ∠BAD = 1/2 (∠A )

Hence, ∠BAD = 60/2 = 30^o

Therefore, ∠BAD equals to 30^o

问题4：检查以下各项中的AD是否为ΔABC的∠A的二等分线：

(i)AB = 5厘米，AC = 10厘米，BD = 1.5厘米，CD = 3.5厘米

解决方案：

Given:

Length of side AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm

To check: whether AD is the bisector of ∠A 

Now,

AB/AC = 5/10 = 1/2

BD/CD = 1.5/3.5 = 3/7

Therefore,

AB/AC ≠ BD/CD

And since ratio between sides are not proportional

Therefore, AD is not the bisector of ∠A

(ii)AB = 4厘米，AC = 6厘米，BD = 1.6厘米，CD = 2.4厘米

解决方案：

Given:

Length of side AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm 

To check: whether AD is the bisector of ∠A 

Now,

AB/AC = 4/6 = 2/3

BD/CD = 1.6/2.4 =2/3

Therefore,

AB/AC = BD/CD

And since ratio between sides are  proportional

Therefore, AD is the bisector of ∠A

(iii)AB = 8厘米，AC = 24厘米，BD = 6厘米，BC = 24厘米

解决方案：

Given:

Length of side AB = 8 cm, AC = 24 cm, BD = 6 cm and BC = 24 cm

To check : whether AD is the bisector of ∠A

Length of side CD = BC – BD= 24 -6 =18cm

CD = 18cm

Now,

AB/AC = 8/24 = 1/3

BD/CD = 6/18 =1/3

Therefore,

AB/AC = BD/CD

And since ratio between sides are proportional

Therefore, AD is the bisector of ∠A

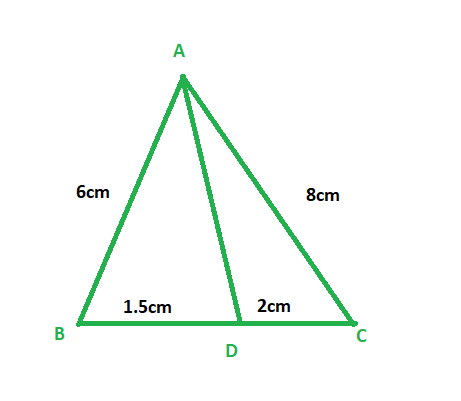
(iv)AB = 6厘米，AC = 8厘米，BD = 1.5厘米，CD = 2厘米

解决方案：

Given:

Length of side AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 2 cm

To check: whether AD is the bisector of ∠A

Now,

AB/AC = 6/8 = 3/4

BD/CD = 1.5/2 =3/4

Therefore,

AB/AC = BD/CD

And since ratio between sides are proportional

Therefore, AD is the bisector of ∠A

(v)AB = 5厘米，AC = 12厘米，BD = 2.5厘米，BC = 9厘米

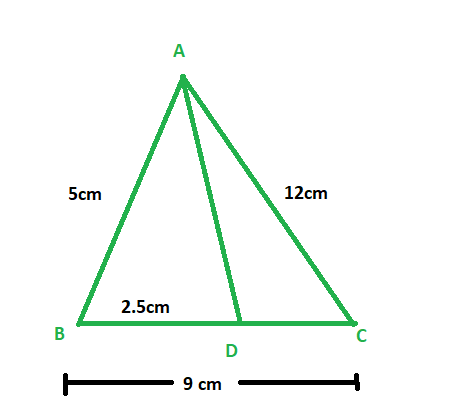
解决方案：

Given:

Length of side AB = 5 cm, AC = 12 cm, BD = 2.5 cm and BC = 9 cm

To check: whether AD is the bisector of ∠A

Length of side CD = BC – BD= 9 – 2.5 = 6.5cm

CD = 6.5cm

Now,

AB/AC = 5/12 = 5/12

BD/CD = 2.5/6.5 =5/13

Therefore,

AB/AC ≠ BD/CD

And since ratio between sides are not proportional

Therefore, AD is not the bisector of ∠A

问题5：在图。 AD二等分∠A，AB = 12厘米，AC = 20厘米，BD = 5厘米，确定CD。

解决方案：

Given: 

Length of side AB = 12 cm, AC = 20 cm, and BD = 5 cm

 AD bisects ∠A

To find: Length of side CD

Since, AD is the bisector of ∠A

Therefore, we get

AB/AC = BD/CD

12/20 = 5/CD

12 × CD = 20 × 5

CD = 100/12

CD = 8.33 cm

∴ CD = 8.33 cm.

Therefore, Length of side CD is 8.33 cm

问题6：在ΔABC中，如果∠1=∠2，

证明AB / AC = BD / CD

解决方案：

Given:

 ∠1 = ∠2

To prove : AB/AC = BD/CD

Construction: Through C , draw CE || BA which meets BA in E on producing the line further

Proof :

Since AD || CE 

Therefore, ∠2 = ∠3        (Alternate angle )

And, ∠1 = ∠4                (Corresponding angle)        

And ∠1 = ∠2           (Given)

Therefore, ∠3 = ∠4 

Since, sides opposite to equal angles are equal

So, AC = AE              – equation 1

Now, in ΔBCE

AD || CE by construction

So, AD is the bisector of ∠A

Therefore, we get

AB/AE = BD/CD

Since, AC = AE from equation 1

 Therefore, AB/AC = BD/CD         

Hence proved

问题7：D和E分别是BC，CA和AB侧的点。一个ΔABC使得AD平分∠A，BE平分的∠B和CF平分∠C。如果AB = 5厘米，BC = 8厘米，CA = 4厘米，请确定AF，CE和BD。

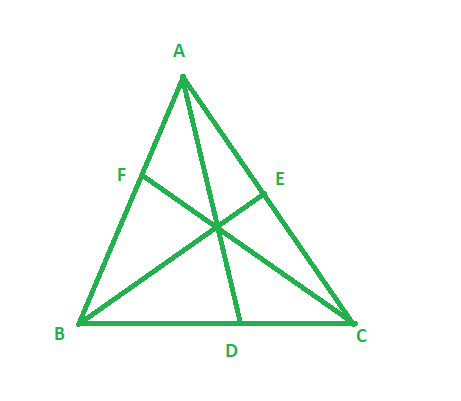
解决方案：

Given:

Length of side AB = 5 cm, BC = 8cm, and CA = 4 cm

AD bisects  ∠A, BE bisects ∠B and CF bisects ∠C

To find: Length of side AF, CE, and BD

Since, AD is the bisector of ∠A

Therefore, we get,

AB/AC = BD/CD

5/4 = BD/ (BC – BD)                      ( Since CD = BC – BD )

5/4 = BD/ (8 – BD)

40 – 5BD = 4BD

9BD = 40

Therefore, BD = 40/9

Since, BE is the bisector of ∠B

Therefore, we get,

AB/BC = AE/EC

5/8 = (AC – EC)/EC                       ( Since AE = AC – EC )

5/8 = (4 – EC)/EC

5EC = 8(4 – EC)

5EC = 32 -8EC

13EC =32

EC = 32/13

Therefore, EC = 32/13

Now, since, CF is the bisector of ∠C

Therefore, we get,

BC/CA = BF/AF

8/4 = (AB – AF)/AF                                  ( Since BF = AB – AF )

2 = (5 – AF)/AF

2AF = 5 – AF

3AF = 5

AF = 5/3

Therefore, AF = 5/3

So length of BD is 40/9cm, EC is 32/13cm and AF is 5/3 cm