问题11。在图中,PQ在圆的点R处以O为中心切线。如果∠TRQ= 30°,则找到m RSPRS
解决方案:
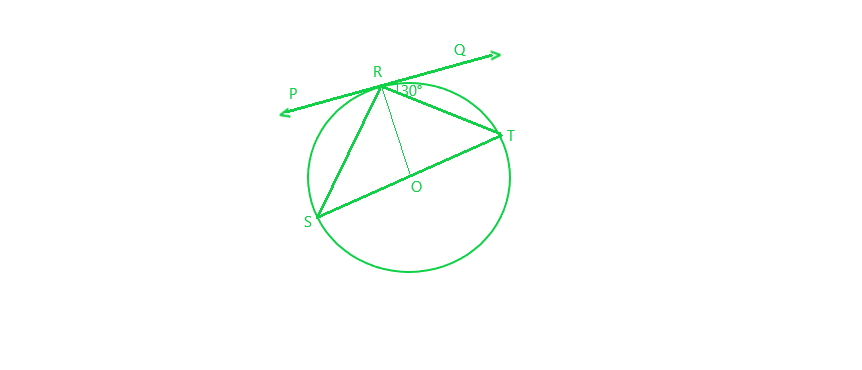
∠TRQ = 30° and PQ is tangent at point R
To Find: ∠PRS
Now ∠SRT = 90° (angle in a semicircle)
Also, ∠TRQ + ∠SRT + ∠PRS = 180° (Angles of a line)
=> 30° + 90° + ∠PRS = 180°
=> ∠PRS = 180° – 120°
=> ∠PRS = 60°
问题12.如果PA和PB是从外点P切线的切线,则PA = 10 cm,∠APB= 60°。求出和弦AB的长度。
解决方案:

PA = 10 cm and ∠APB = 60°
We also know that
PA = PB = 10 cm (Tangents drawn from a point outside the circle are equal)
=> ∠PAB = ∠PBA
Now, In ∆APB, we have:
∠APB + ∠PAB + ∠PBA = 180° (Angles of a triangle)
=> 60° + ∠PAB + ∠PAB = 180°
=> 2 ∠PAB = 180° – 60° = 120°
=> ∠PAB = 60°
∠PBA = ∠PAB = 60°
Hence. PA = PB = AB = 10 cm
Thus, length of chord AB = 10 cm
问题13:在∠B= 90°的直角三角形ABC中,画出一个圆,其AB的直径与P处的斜边AC相交。证明在P处的圆切线将BC切成两等分。
解决方案:
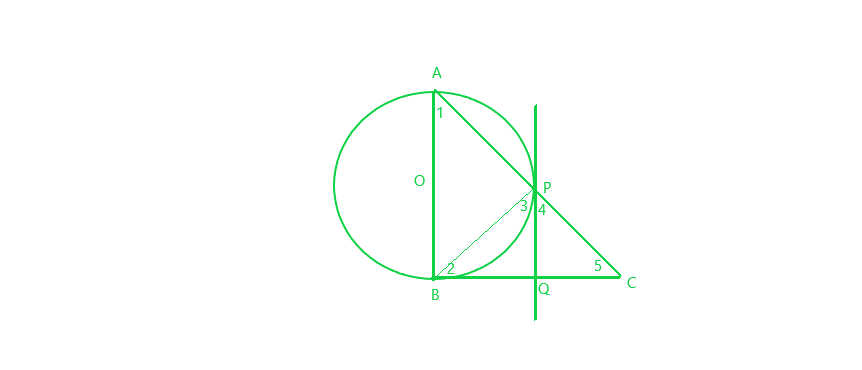
Given: Let O be the centre of the circle with diameter AB.
Tangents to the circle at P meets BC at Q.
To Prove: PQ bisects BC, i.e., BQ = QC
Proof:
∠ABC = 90°
In ∆ABC, ∠1 + ∠5 = 90° [angle sum property, ∠ABC = 90°]
∠3 = ∠1 [angle between tangent and the chord equals angle made by the chord in alternate segment]
=> ∠3 + ∠5 = 90° (1)
And, ∠APB = 90° [angle in semi-circle]
=> ∠3 + ∠4 = 90° (2) [∠APB + ∠BPC = 180°, linear pair]
From Equation (1) and (2), we get
∠3 + ∠5 = ∠3 + ∠4
∠5 = ∠4
=> PQ = QC (3) [sides opposite to equal angles are equal]
Also, QP = QB (4) [tangents drawn from an internal point to a circle are equal]
From equation (3) and (4), we get:
=> QB = QC
Thus, PQ bisects BC is proved
问题14.从外部点P将切线PA和PB绘制到以O为中心的圆上。如果CD是在点E处与圆的切线且PA = 14 cm,则找到∆PCD的周长。
解决方案:
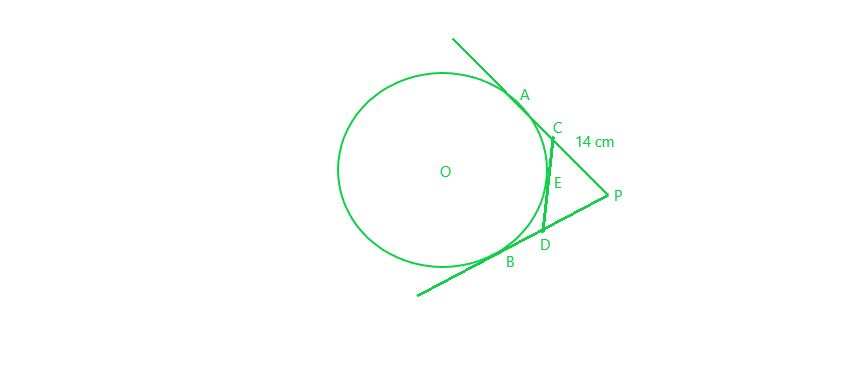
PA = 14 cm
PA = PB = 14 cm (PA and PB are the tangents to the circle from P)
Also,
CA = CE (1) (CA and CE are the tangents from C)
DB = DE (2) (DB and DE are the tangents from D)
So, perimeter of ∆PCD:
= PC + PD + CD
=> PC + PD + CE + DE
=> PC + CE + PD + DE
=> PC + CA + PD = DB (From (1) and (2))
=> PA + PB
=> 14 cm + 14 cm
= 28 cm
问题15。在图中,ABC是在B处成直角的直角三角形,使得BC = 6 cm,AB = 8 cm。找到其圆的半径。
解决方案:
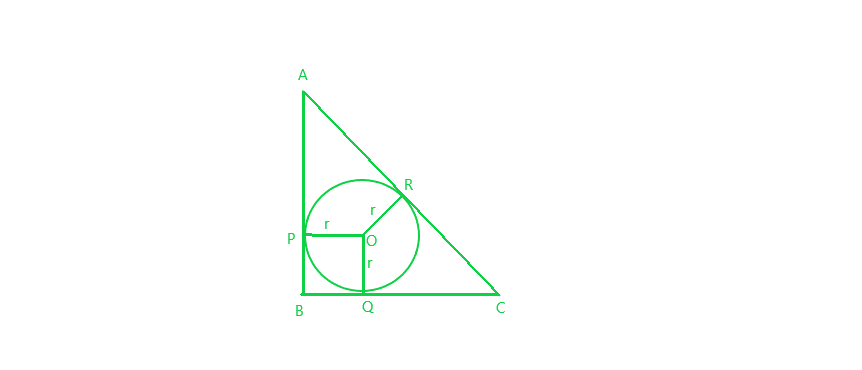
∠B = 90°, BC = 6 cm, AB = 8 cm and r be the radius of incircle with centre O
Applying Pythagoras Theorem in right-angled ∆ABC:
AC² = AB² + BC²
=> AC² = (8)² + (6)² = 64 + 36 = 100
=> AC = 10 cm
=> AR + CR = 10 cm (1)
Now, AP = AR (AP and AR are the tangents to the circle from A)
Similarly, CR = CQ and BQ = BP
OP and OQ are radii of the circle = r (2)
OP ⊥ AB and OQ ⊥ BC (3) (angle between the radius to the point of contact of tangent is 90°)
and ∠B = 90° (4)
From equation (2), (3) and (4):
BPOQ is a square
=> BP = BQ = r
=> AR = AP = AB – BD = 8 – r (5)
and CR = CQ = BC – BQ = 6 – r (6)
From equation (1), (5) and (6), we get:
AR + CR = 10
=> 8 – r + 6 – r = 10 (from (5) and (6))
=> 14 – 2r = 10
=> 2r = 14 – 10 = 4
=> r = 2
Radius of the incircle = 2 cm
问题16.证明在圆弧的中点处绘制的切线平行于连接圆弧端点的弦。
解决方案:
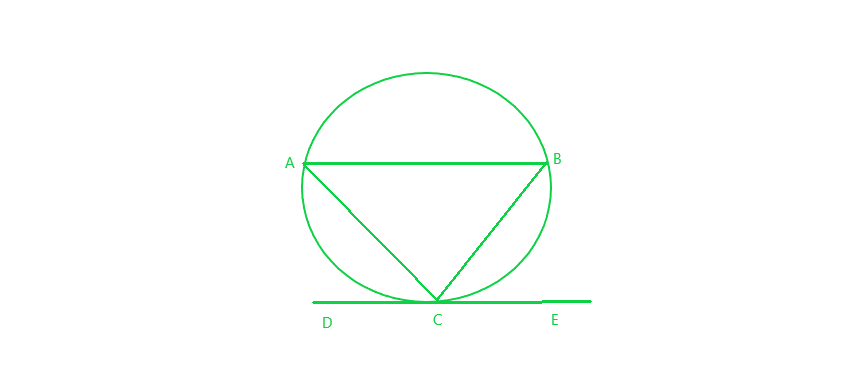
Given: Let mid-point of arc ACB be C and, DCE be the tangent to it
To prove: AB || DCE
Proof:
Arc AC = Arc BC
=> Chord AC = Chord BC
Now, In ∆ABC,
AC = BC
=> ∠CAB = ∠CBA (1) (equal sides corresponding to the equal angle)
Since, DCE is a tangent line.
∠ACD = ∠CBA (angle in alternate segment are equal)
=> ∠ACD = ∠CAB (from Eq. (1))
=> ∠ACD and ∠CAB are alternate angles
Which is only possible only when AB || CDE
Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
问题17.从点P开始,将两个切线PA和PB绘制到一个以O为中心的圆上。如果OP =圆的直径,则表明ΔAPB是等边的。
解决方案:
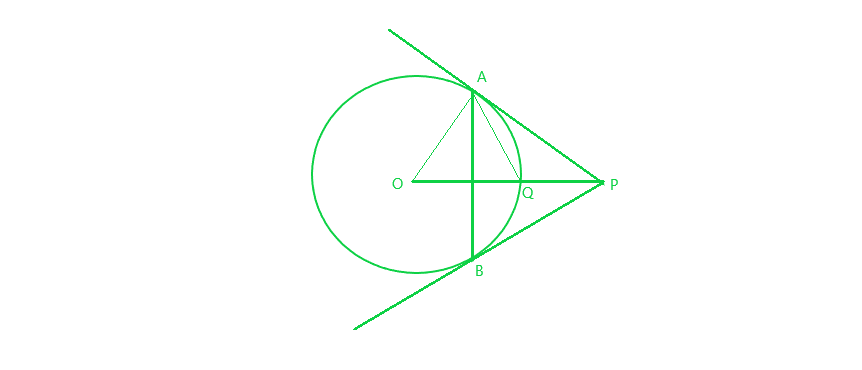
Given : Two tangents PA and PB are drawn to the circle and OP is diameter
To prove: ∆APB is equilateral
Proof: OP = 2r (let r be the radius of the circle)
=> OQ + QP = 2r
=> OQ = QP = r (OQ is the radius)
Now in right ∆OAP,
OP is the hypotenuse and Q is the mid point of it
=> OA = AQ = OQ (mid-point of hypotenuse of a right triangle is equidistant from its vertices)
Thus, ∆OAQ is equilateral triangle
=> ∠AOQ = 60°
Also, ∠APO = 90° – 60° = 30° (Sum of all the angles of triangle is 180° )
=> ∠APB = 2 ∠APO = 2 x 30° = 60° (1)
We also know that, PA = PB (Tangents from P to the circle)
=> ∠PAB = ∠PBA (2)
Now, in ∆APB:
∠PBA + PAB + ∠APB = 180° (Sum of all angles)
=> 2∠PBA = 120° (from (1) and (2))
=> ∠PAB = ∠PBA = 60°
Hence, ∆APB is an equilateral triangle.
问题18:将两个切线段PA和PB绘制到一个以O为中心的圆上,使得∠APB= 120°。证明OP = 2 AP。
解决方案:
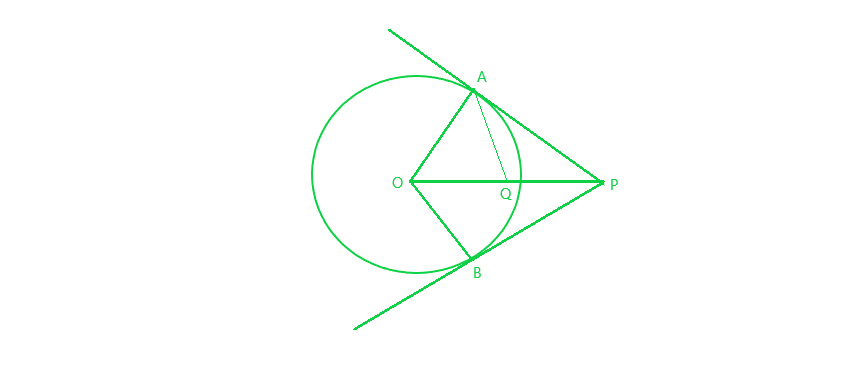
Given : Two tangents to the circle from a point P and ∠APB = 120°
To prove : OP = 2 AP
Proof : In right ∆OAP,
∠OPA = (1/2)∠APB = 60°
=> ∠AOP = 90° – 60° = 30°
Let, Q be mid point of hypotenuse OP of ∆OAP
=> QO = QA = QP
=> ∠OAQ = ∠AOQ = 30°
=> ∠PAQ = 90° – 30° = 60°
So, ∆AQP is an equilateral triangle
=> QA = QP = AP (1)
Also, Q is mid point of OP
=> OP = 2 QP = 2 AP (from (1))
Hence, proved.
问题19:如果ΔABC是等腰线,且AB = AC,并且C(0,r)是ΔABC接触L处BC的内切线。证明L将BC对等。
解决方案:
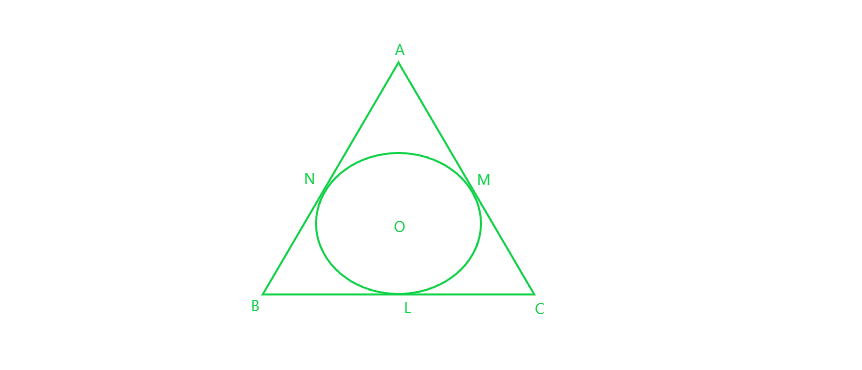
Given: ∆ABC isosceles with AB = AC and incircle with centre O and radius r touches the side BC of ∆ABC at L.
To prove : L is mid point of BC.
Proof : AM and AN are the tangents to the circle from A
=> AP = AQ
But AB = AC (given)
=> AB – AQ = AC – AP
=> BQ = CP (1)
Now BL and BQ are the tangents from B
=> BL = BQ (2)
Similarly, CL and CP are tangents
=> CL = CP (3)
Also, BQ = CP (from (1))
=> BL = CL (from (2) and (3))
Hence, proved that L is mid point of BC.