第11类RD Sharma解决方案–第23章直线-练习23.5

问题1.找到通过以下两对点的直线方程。

(i)(0，0)和(2，-2)

解决方案：

Here, the two points are (x₁, y₁) = (0, 0) and (x₂, y₂) = (2, -2).

So the equation of the line in two point form is

y – y₁ = (y₂ – y₁) / (x₂ – x₁)(x – x₁)  

y – 0 = [(-2 – 0)/(2 – 0)] (x – 0)

⇒ y = (-1)x

⇒ y = -x

(ii)(a，b)和(a + c sinα，b + c cosα)

解决方案：

Here, the two points are (x₁, y₁) = (a, b) and (x₂, y₂) = (a + c sin α, b + c cos α).

So the equation of the line in two point form is

y – b = (b + c cos α – b)/(a + c sin α – a)(x- a)

⇒ y – b = (cos α/sin α)(x – a)

⇒ y – b = cot α(x – a)

(iii)(0，-a)和(b，0)

解决方案：

Here, the two points are (x₁, y₁) = (0, -a) and (x₂, y₂) = (b, 0).

So the equation of the line in two point form is

y – (-a) = (0 – (-a))/(b – 0)(x – 0)

⇒ b(y + a) = ax

⇒ ax – by = ab

(iv)(a，b)和(a + b，a – b)

解决方案：

Here, the two points are (x₁, y₁) = (a, b) and (x₂, y₂) = (a + b, a – b).

So the equation of the line in two point form is

y – b = (a – b – b)/(a + b – a)(x – a)

⇒ y – b = (a – 2b)/b (x – a)

⇒ y – b = (a – 2b)x + a² – 2ab

⇒ (a – 2b)x – by + b² + 2ab – a² = 0

(v)(在₁ ，a / t ₁ )和(在₂ ，a / t ₂ )

解决方案：

Here, the two points are (x₁, y₁) = (at₁, a/t₁) and (x₂, y₂) = (at₂, a/t₂).

So the equation of the line in two point form is

y – a/t₁ = (a/t₂ – a/t₁) / (at₂ – at₁)(x – at₁)  

⇒ y – a/t₁ = ((at₁ – at₂)/t₁t₂)/(at₂ – at₁)(x – at₁)

⇒ t₁t₂y – at₂ = (-1)(x – at₁)

⇒ t₁t₂y + x = at₁ + at₂

(vi)(一个cosα，一个sinα)和(一个cosβ，一个sinβ)

解决方案：

Here, the two points are (x1, y1) = (a cos α, a sin α) and (x2, y2) = (a cos β, a sin β).

So the equation of the line in two point form is

y – a sin α =(a sin β – a sin α)/(a cos β – a cos α)(x – a cos α)  

⇒ y – a sin α = [2cos (β + α)/2 sin (β – α)/2] / [-2sin (β + α)/2 sin (β – α)/2](x – a cos α)

⇒ y – a sin α = -[cos (β + α)/2]/[sin (β + α)/2](x – a cos α)

⇒ x cos (β + α)/2 + y sin (β + α)/2 = a(sin α [sin (β + α)/2] + cos α [cos (β + α)/2])

⇒ x cos (β + α)/2 + y sin (β + α)/2 = a cos (α – β/2 – α/2)

⇒ x cos (β + α)/2 + y sin (β + α)/2 = a cos (α/2 – β/2)

问题2。在三角形的边上分别找到方程，其角点分别为坐标。

(i)(1、4)，(2，-3)和(-1，-2)

解决方案：

Given: Points A (1, 4), B (2, -3) and C (-1, -2). 

Equation of the line passing through the two points (x₁, y₁) and (x₂, y₂)  

y – y₁ = [(y₂ – y₁)/(x₂ – x₁)] (x – x₁) 

Equation of the sides AB, 

By using the above formula 

y – 4 = [(-3 – 4)/(2 – 1)](x – 1)

⇒ y – 4 = -7x + 7

⇒ y + 7x = 11

Similarly

 Equation of the sides BC

 ⇒ y + 3 = [(-2 – (-3))/(-1 – 2)](x – 2) 

y + 3 = (-1/3) (x – 2) 

⇒ 3y + 9 = -x + 2 

⇒ 3y + x = – 7

⇒ x + 3y + 7 = 0 

And equation of the sides CA 

⇒ y + 2 = [(4 – (-2))/(1 – (-1))](x + 1) 

⇒ y + 2 = 3(x + 1)

⇒ y + 2 = 3x + 3

⇒ y – 3x = 1 

The equation of the required sides of the triangle are y + 7x = 11, x+ 3y + 7 =0 and y – 3x = 1

(ii)(0，1)，(2，0)和(-1，-2)

解决方案：

Given, Points A (0, 1), B (2, 0) and C (-1, -2). 

The equation of the line passing through the two points (x₁, y₁) and (x₂, y₂) 

 y – y₁ = [(y₂ – y₁)/(x₂ – x₁)] (x – x₁) 

Equation of the sides AB,

By using the above formula 

 y – 1 = [(0 – 1)/(2 – 0)](x – 0) 

⇒ y – 1 = -1/2 x 

⇒ 2y – 2 = -x 

⇒ x + 2y = 2 

Equation of the sides BC

y – 0 = [(-2 – 0)/(-1 – 2)](x – 2) 

⇒ y – 0 = (-2/3)(x – 2) 

⇒ 3y = -2x + 4

⇒ 2x – 3y = 4 

Equation of the sides CA

⇒ y – (-2) = [(1 + 2)/(1 + 0)](x – (-1))

⇒ y + 2 = 3(x + 1) 

⇒ y + 2 = 3x + 3 

⇒ y – 3x = 1

The required equation of sides of the triangle are x + 2y = 2, 2x – 3y = 4, and y – 3x = 1

问题3。找到一个三角形的中位数方程，该三角形的顶点坐标为(-1，6)，(-3，-9)和(5，-8)。

解决方案：

Let A (−1, 6), B (−3, −9) and C (5, −8) be the coordinates of the given triangle and 

D, E, and F be midpoints of AB, BC and AC, respectively. 

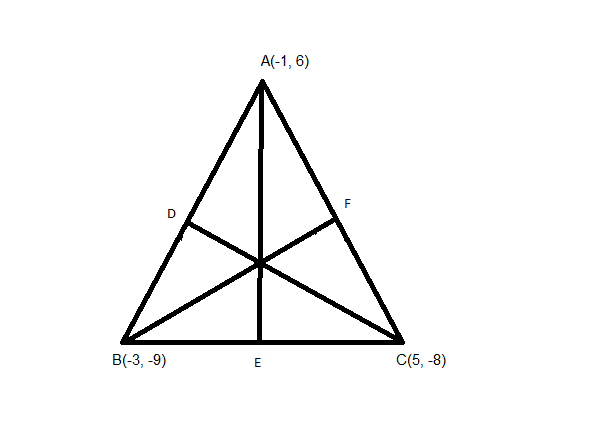
Coordinate of midpoint of AB = D[(-1 – 3)/2, (6 – 9)/2]

= D(-2, -3/2) 

Median CD passes through C (5, -8) and D(-2, -3/2)

So, by using the formula (y – y₁) = [(y₂ – y₁)/(x₂ – x₁)] (x – x₁) 

(y – (-8)) = [(-3/2 – (-8))/(-2 – 5)] (x – 5)

⇒ y + 8 = -13/14(x-5)

⇒ 14y + 112 = -13x + 65

⇒ 13x + 14y + 47 = 0

Coordinate of midpoint of BC = E[(-3 + 5)/2, (-9 – 8)/2]

= E(1, -17/2) 

Median AE passes through A (-1, 6) and E (1, -17/2) 

Using the two point formula

⇒ y – 6 = -29/4 (x + 1)

⇒ 4y – 24 = -29x – 29 

⇒ 29x + 4y + 5 = 0

Coordinate of midpoint of AC = F[(-1 + 5)/2, (6 – 8)/2]

= E(2, -1) 

Similarly, Median BF passes through B (-3,-9) and F (2,-1) 

By using the formula, 

y – (-9) = [(-1 – (-9))/(2 – (-3))] (x – (-3)) 

⇒ y + 9 = 8/5 (x + 3)

⇒ 5y + 45 = 8x + 24

⇒ 8x – 5y – 21 = 0

The equation of the required medians of triangle are: 29x + 4y + 5 = 0, 8x – 5y – 21 = 0, and 13x + 14y + 47 = 0

问题4。找到矩形对角线的方程，该矩形的边为x = a，x = a’，y = b和y = b’。

解决方案：

Given,

Equation of sides of the rectangle are x = a, x = a’, y = b and y = b’ 

Thus, the vertices of the rectangle are A (a, b), B (a’, b), C (a’, b’) and D (a, b’)

 Equation of the diagonal passing through A (a, b) and C (a’, b’) 

 By using the formula (y – y₁) = [(y₂ – y₁)/(x₂ – x₁)] (x – x₁) 

⇒ y – b = [(b’ – b)/(a’ – a)] (x – a)

⇒ (a’ – a)y – b(a’ – a) = (b’ – b)x – a(b’ – b) 

⇒ (a’ – a) – (b’ – b)x = ba’ – ab’ 

Similarly, equation of diagonal passing through B (a’, b) and D (a, b’)

 By using the two point formula, 

⇒ y – b = [(b’ – b)/(a – a’)] (x – a’)

⇒ (a – a’)y – b(a – a’) = (b’ – b)x – a’ (b’ – b) 

⇒ (a’ – a)y + (b’ – b)x = a’b’ – ab 

The required equation of diagonals are y(a’ – a) – x(b’ – b) = a’b – ab’ and y(a’ – a) + x(b’ – b) = a’b’ – ab

问题5。找到三角形ABC的边BC的方程，其顶点分别为A(-1，-2)，B(0，1)和C(2，0)。另外，找到通过(-1，-2)的中值方程。

解决方案：

Equation of side BC of the triangle ABC is

(y – 1) = [(0 – 1)/(2 – 0)] (x – 0)

⇒ (y – 1) = (-1/2)x

⇒ x + 2y – 2 = 0

Mid point of (0, 1) and (2, 0)

= [(0 + 2)/2, (1 + 0)/2]

= (1, 1/2)

Equation of median through (-1, -2) and (1, 1/2)

(y – (-2)) = [(1/2 + 2)/(1 + 1)](x – (-1))

⇒ y + 2 = 5/4(x + 1)

⇒ 4y + 8 = 5x + 5

⇒ 5x – 4y – 3 = 0 is the required equation of median.

问题6。通过使用线方程的概念，证明三个点(3，0)，(-2，-2)和(8，2)是共线的。

解决方案：

To show that the points(-2, -2), (8, 2) and (3, 0) are collinear,

The equation of the line passing through points (3, 0), (-2, -2) is

(y − 0) = [(−2 − 0)/(−2 − 3)](x − 3)

y = -2/−5(x − 3)

5y = 2x − 6

2x − 5y = 6

Now, putting the third point in the above equation to check if it satisfies or not.

L.H.S. = 2 × 8 − 5 × 2

= 16 − 10

= 6 = R.H.S.

Therefore, the line passing through points (3, 0) and (-2, -2) also passes through point (8, 2).

Hence, points (3,0), (-2, -2) and (8, 2) are collinear.

问题7.证明线y-x + 2 = 0将点(3，-1)和(8，9)的连接按比例2：3划分。

解决方案：

Suppose the line y- x+ 2=0 divides the join of points (3, -1) and (8, 9) in the ratio 2:3. 

The coordinate of point of division must lie on the given line.

 Coordinate of point of division = [(8×2+ 3×3) / (2+3), (9×2-3) / (2+ 3)]

= (25/5, 15/ 5) = (5, 3)

Putting this coordinate in y – x + 2 = 0 

= 3 – 5 + 2

= -2 + 2 = 0

Thus, we see that the coordinate satisfies the r = equation of line which 

proves that line divides the join of points in the ratio of 2:3.

问题8.在直线上找到方程，该方程将点(a，b)和(a’，b’)之间的距离二等分，还将点(-a，b)和(a’，–之间的距离二等分b’)。

解决方案：

The points which bisects the given points are (x1, y1) = (a + a′/2, b + b′/2) and (x2, y2) = (-a + a′/2, b − b′/2) 

Using the two point formula  

(y − y₁) = [(y₂ − y₁)/(x₂ − x₁)](x − x₁) 

[y – (b + b’)/2] = $[\frac{\frac{(b − b′ − b − b′)}{2}}{\frac{(−a + a′ − a − a′)}{2}} ] [x-\frac{(a+ a')}{2}]$

⇒ (2y – b – b’)/2 = b’/a (2x – a – a’)/2

⇒ 2ay – ab – ab’ = 2b’x – ab’ – a’b’

⇒ 2ay – 2b’x + a’b’ – ab = 0 Is the required equation of the straight line

问题9：连接点(2、3)和(4，-5)的线除以穿过点(6、8)和(-3，-2)的线的比率是多少。

解决方案：

Equation of the line joining (6, 8) and (-3, -2)

y – 8 = [(-2 – 8)/(-3-  6)](x – 6)

⇒ Y – 8 = 10/9(x – 6)

⇒ 9Y – 72 = 10x – 60

⇒ 10x – 9y + 12 = 0

Let the ratio in which the points (2, 3) and (4, -5) divided by k : 1

P[(4k + 2)/(k + 1), (-5k + 3)/(k + 1)]

We put this point in the above straight line as it satisfies the above equation

 10 (4k + 2)/(k + 1) – 9(-5k + 3)/ (k + 1) + 12 = 0

40k + 20 + 45k – 27 + 12k + 12 = 0

97k + 5 = 0

k = -5/97

or k = 5/97 (External)

问题10.四边形的顶点是A(-2，6)，B(1，2)C(10，4)和D(7，8)。求出其对角线的等式。

解决方案：

Given A(−2, 6), B(1, 2), C(10, 4) and D(7, 8)

Diagonals are AC and BD

Equation of line AC

y − 6 = [(4 – 6)/(10 – (-2))] (x − (-2))

⇒ y − 6 = (-2/12)(x + 2)

⇒ 6y – 36 = -x – 2

⇒ x + 6y − 34 = 0

Equation of line BD

y − 2 = [(8 – 2)/(7 – 1)] (x − 1)

⇒ y – 2 =(6/6)(x- 1)

⇒ y – 2 = x – 1

⇒ x − y + 1 = 0

So the required equation are x + 6y − 34 = 0 and x − y + 1 = 0

问题11.铜棒的长度L(厘米)是其摄氏温度C的线性函数。在实验中，如果当C = 20时L = 124.942，当C = 110时L = 125.134，则用以下公式表示L： C。

解决方案：

Let us assume C to be along the x-axis and L along the y-axis

 We have two points (20, 124.942) and (110, 125.134) 

The linear relation between L and C is given by the equation of 

the line passing through points (20, 124.942) and (110, 125.134)

(L− 124.942) = (125.134 − 124.942) / (110 − 20)(C − 20)

⇒ L −124.942 = 0.192/90(C − 20)

⇒ L = 0.192/ 90(C − 20) + 124.942 is the required linear relation.

问题12.一家牛奶店的所有者发现，他每周可以出售980升牛奶，每公升14卢比，出售1220升牛奶，每公升16卢比。假设售价与需求之间存在线性关系，那么他每周可以以每升17卢比的价格出售多少升水?

解决方案：

Given, 

980 liters of milk sells out at Rs 14 per liter

1220 liters of milk sells out at Rs 16 per liter

Let us assume amount of milk on y-axis and selling price on x-axis.

We can say the line passes through A(14, 980), B(16, 1220) and C(17, x)

Since there is a linear relationship between selling price and demand

Therefore, Slope of AB= Slope BC

(1220 – 980)/(16 – 14) = (x – 1220)/(17 – 16)

⇒ 240/2 = x – 1220 / 1

x = 1340 liters of milk he could sell weekly at Rs 17 per liter 

问题13。找到顶点为A(4，3)，B(0，0)和C(2，3)的三角形的角度A的平分线方程。

解决方案：

Let AD be the bisector of angle A

Then BD : DC = AB : AC

|AB| = √((4 – 0)² + (3 – 0)²) = 5

|AC| = √((4 – 2)² + (3 – 3)²) = 2

⇒ BD/DC = AB/AC = 5/2

i.e. D divides BC in the ratio of 5:2

Now, coordinate of D are \frac{(5×2 +0)}{5+2}, \frac{(5×3+0)}{5+2} = (10/7, 15/7)

The required equation of the bisector AD=

Using the two point formula

y – 3 = [$\frac{(\frac{15}{7} - 3)}{(\frac{10}{7} - 4)}$)](x – 4)

⇒ y – 3 = [(15 – 21)/(10 – 28)](x – 4)

⇒ y – 3 = 1/3 (x – 4)

⇒ 3y – 9 = x – 4

⇒ x – 3y + 5 = 0

问题14：找到经过原点的直线方程，并将直线3x + y = 12的部分三等分，该部分在坐标轴之间截取。

解决方案：

To find the interception point we put x = 0 and y = 0.

3x + y = 12

x = 0 ⇒ y = 12

y = 0 ⇒ x = 4

So the line is intercepted between A(4, 0) and B(0, 12)

Let the points P and Q trisect the portion of the line AB

Now P divides AB in 1:2

= P \frac{(1(0) + 2(4))}{(1 + 2)}, \frac{(1(12) + 2(0))}{(1 + 2)}

= P(8/3, 4)

So the equation of line joining origin and P is  

y − 0 = [(4 – 0)/(8/3 – 0)](x – 0)

y = (12/8)x = (3/2)x

Now Q divides AP in 1:1, 

= Q[(8/3 + 0)/2, (4 + 12)/2]

= Q(4/3, 8)

The equation of line joining origin to Q is  

y – 0 = [(8 – 0)/(4/3 – 0)](x – 0) 

y = (24/4)x = 6x

So, the required equations are y = 6x and 2y = 3x.

问题15。找到由线x = 0，y = 0，x = 1和y = 1构成的正方形的对角线方程。

解决方案：

From the graph, we get four points, i.e., A(0, 1), B(1, 1), C(1, 0), and D(0, 0).

Now let us considered D1 is the diagonal formed by joining B and D point, 

and D2 is the diagonal formed by A and C points.

So, we find the equation of D1 diagonal:

(y – 1) = $\frac{(0 - 1)}{(0 - 1)} (x-1)$

(y – 1) = (1)(x – 1)

y = x

 So, we find the equation of D2 diagonal:

(y – 1) = $\frac{(0 - 1)}{(1 - 0)} (x-0)$

(y – 1) = (-1)(x)

y + x = 1