11类NCERT解决方案-第8章二项式定理–第8章的其他练习

问题1.如果扩展的前三个项分别为729、7290和30375，则在^{(a + b)n}的扩展中找到a，b和n。

解决方案：

As, we know that (r+1)^th term of (a+b)ⁿ is denoted by,

T_r+1 = ⁿC_r a^n-r b^r

Here, it is given that first three terms of the expansion are 729, 7290 and 30375.

When, T₁ = 729, T₂ = 7290 and T₃ = 30375

T₀₊₁ (r=0) = ⁿC₀ a^n-0 b⁰ = aⁿ = 729  …………………(1)

T₁₊₁ (r=0) = ⁿC₁ a^n-1 b¹ = na^n-1 b = 7290  …………………(2)

T₂₊₁ (r=0) = ⁿC₂ a^n-2 b² = $\frac{n!}{2!(n-2)!}$a^n-2b² = $\frac{n(n-1)a^{n-2}b^2}{2}$ = 30375  …………………(3)

Dividing (1) and (2), we get

$\frac{na^{n-1} b}{a^n} = \frac{7290}{729}$

na^n-1-n b = 10

$\frac{nb}{a}$ = 10 ……………………….(I)

Now, dividing (3) and (2), we get

$\frac{\frac{n(n-1)a^{n-2}b^2}{2}}{na^{n-1} b} = \frac{30375}{7290}$

$\frac{(n-1)b}{2a} = \frac{30375}{7290}$

$\frac{nb-b}{a} = \frac{25}{3}$

$\frac{nb}{a} - \frac{b}{a} = \frac{25}{3}$

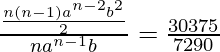
From (I), we can substitute

$10 - \frac{b}{a} = \frac{25}{3}$

$\frac{b}{a}$ = 10 – $\frac{25}{3}$

$\frac{b}{a} = \frac{30-25}{3} = \frac{5}{3}$ ………………….(II)

Substituting (II) in (I), we get

$\frac{nb}{a}$ = 10

$n(\frac{5}{3})$ = 10

n = $\frac{10 \times3}{5}$

n = 6

Substituting n = 6 in (1), we get

aⁿ = 729

a⁶ = 729

a = 3

Substituting a = 3 in (II), we get

$\frac{b}{a} = \frac{5}{3}$

b = $\frac{5\times3}{3}$

b = 5

Hence, a = 3, b = 5 and n = 6

问题2。找出(3 + ax) ^{9的展开式中x 2}和x ³的系数是否相等。

解决方案：

As, we know that (r+1)^th term of (a+b)ⁿ is denoted by,

T_r+1 = ⁿC_r a^n-r b^r

Here, a = 3 and b = ax and n = 9.

T_r+1 = ⁹C_r 3^9-r (ax)^r

T_r+1 = ⁹C_r $(\frac{3^9}{3^r})$ a^rx^r

T_r+1 = ⁹C_r $(\frac{3^9 \times a^r}{3^r}) x^r$

So, here if you want the power of x² and x³. Then r=2 and r=3.

r = 2, T_{2+1 =} $[^9C_2 (\frac{3^9 \times a^2}{3^2})] x^2$

r = 3, T₃₊₁ = $[^9C_3 (\frac{3^9 \times a^3}{3^3})] x^3$

Coefficient of x² = Coefficient of x³

$^9C_2 (\frac{3^9 \times a^2}{3^2}) = ^9C_3 (\frac{3^9 \times a^3}{3^3})$

$\frac{9!}{2! (9-2)!} \times \frac{3^9 \times a^2}{3^2} = \frac{9!}{3! (9-3)!} \times \frac{3^9 \times a^3}{3^3}$

$\frac{1}{2! (9-2)!} \times \frac{a^2}{3^2} = \frac{1}{3! (9-3)!} \times \frac{a^3}{3^3}$

$\frac{3! (9-3)!}{2! (9-2)!} = \frac{a^3 \times 3^2}{a^2 \times 3^3}$

$\frac{a}{3} = \frac{3! 6!}{2! 7!}$

$\frac{a}{3} = \frac{3}{7}$

a = $\frac{3\times 3}{7} = \frac{9}{7}$

Hence, a = $\frac{9}{7}$

问题3.使用二项式定理求出乘积(1 + 2x) ⁶ (1 – x) ^{7中x 5的系数。}

解决方案：

For getting the coefficient of x⁵, lets expand both the binomials for more clear understanding.

(1 + 2x)⁶ = ⁶C₀ + ⁶C₁ (2x) + ⁶C₂ (2x)² + ⁶C₃ (2x)³ + ⁶C₄ (2x)⁴ + ⁶C₅ (2x)⁵ + ⁶C₆ (2x)⁶

= 1 + 6 (2x) + 15 (2x)² + 20 (2x)³ + 15 (2x)⁴ + 6 (2x)⁵ + (2x)⁶

= 1 + 12 x + 60x² + 160 x³ + 240 x⁴ + 192 x⁵ + 64x⁶

(1 – x)⁷ = ⁷C₀ – ⁷C₁ (x) + ⁷C₂ (x)² – ⁷C₃ (x)³ + ⁷C₄ (x)⁴ – ⁷C₅ (x)⁵ + ⁷C₆ (x)⁶ – ⁷C₇ (x)⁷

= 1 – 7x + 21x² – 35x³ + 35x⁴ – 21x⁵ + 7x⁶ – x⁷

Now, the product will be seen as follows

(1 + 2x)⁶ (1 – x)⁷ = (1 + 12 x + 60x² + 160 x³ + 240 x⁴ + 192 x⁵ + 64x⁶) (1 – 7x + 21x² – 35x³ + 35x⁴ – 21x⁵ + 7x⁶ – x⁷)

Here, what we can see that x⁵ will be obtained when two terms will be multiplied of having sum of power of x as 5. Those two terms will be as follows:

First binomial	Second binomial
1st term	6th term
2nd term	5th term
3rd term	4th term
4th term	3rd term
5th term	2nd term
6th term	1st term

So, 

Coefficient of x⁵ = (1)(-21) + (12)(35) + (60)(-35) + (160)(21) + (240)(-7) + (192)(1)

Coefficient of x^{5 =} -21 + 420 – 2100 + 3360 – 1680 + 192

Coefficient of x⁵ = -21 + 420 – 2100 + 3360 – 1680 + 192

Coefficient of x⁵ = 171

Hence, the coefficient of x⁵ in the expression (1+2x)⁶ (1-x)⁷ is 171.

问题4.如果a和b是不同的整数，则只要n是正整数^{，就证明a – b是n} – b ^{n的因数。}

[提示写一个= =(a – b + b) ⁿ并展开]

解决方案：

To prove that (a – b) is a factor of (aⁿ – bⁿ), 

aⁿ – bⁿ = k (a – b) where k is some natural number or constant.

a can be written as = a – b + b

aⁿ = (a – b + b)ⁿ = [(a – b) + b]ⁿ

[(a – b) + b]ⁿ = ⁿC₀ (a – b)ⁿ + ⁿC₁ (a – b)^n-1 b + ……….ⁿC_n-1(a – b)b^n-1 + ⁿC_n bⁿ

aⁿ = (a – b)ⁿ + n (a – b)^n-1 b + ……….ⁿC_n-1(a – b)b^n-1 + bⁿ

Now, aⁿ – bⁿ will be

aⁿ – bⁿ = [(a – b)ⁿ + n (a – b)^n-1 b + ……….ⁿC_n-1(a – b)b^n-1 + bⁿ] – bⁿ

aⁿ – bⁿ = (a – b)ⁿ + n (a – b)^n-1 b + ……….ⁿC_n-1(a – b)b^n-1

Taking (a-b) common, we have

aⁿ – bⁿ = (a – b) [(a –b)^n-1 + n (a – b)^n-2 b + …… + ⁿC_n-1 b^n-1]

aⁿ – bⁿ = (a – b) k

Where k = [(a –b)^n-1 + n (a – b)^n-2 b + …… + ⁿC_n-1 b^n-1] is a natural number

Hence, it is proved a – b is a factor of aⁿ – bⁿ, where n is a positive integer

问题5.评估(√3+√2) ⁶ −(√3−√2) ⁶ 。

解决方案：

Using binomial theorem the expression (a + b)⁶ and (a – b)⁶, can be expanded as follows:

(a + b)⁶ = ⁶C0 a⁶ + ⁶C₁ a⁵ b + ⁶C₂ a⁴ b² + ⁶C₃ a³ b³ + ⁶C₄ a² b⁴ + ⁶C₅ a b⁵ + ⁶C₆ b⁶

(a – b)⁶ = ⁶C₀ a⁶ – ⁶C₁ a⁵ b + ⁶C₂ a⁴ b² – ⁶C₃ a³ b³ + ⁶C₄ a² b⁴ – ⁶C₅ a b⁵ + ⁶C₆ b⁶

Now adding them,

(a + b)⁶ – (a – b)⁶ = ⁶C₀ a⁶ + ⁶C₁ a⁵ b + ⁶C₂ a⁴ b² + ⁶C₃ a³ b³ + ⁶C₄ a² b⁴ + ⁶C₅ a b⁵ + ⁶C₆ b⁶ – [⁶C₀ a⁶ – ⁶C₁ a⁵ b + ⁶C₂ a⁴ b² – ⁶C₃ a³ b³ + ⁶C₄ a² b⁴ – ⁶C₅ a b⁵ + ⁶C₆ b⁶]

(a + b)⁶ – (a – b)⁶ = 2[⁶C₁ a⁵ b + ⁶C₃ a³ b³ + ⁶C₅ a b⁵]

Substituting a = √3 and b = √2, we get

(√3 + √2)⁶ – (√3 – √2)⁶ = 2 [6 (√3)⁵ (√2) + 20 (√3)³ (√2)³ + 6 (√3) (√2)⁵]

= 2 [54(√6) + 120 (√6) + 24 √6]

= 2 (√6) (198)

= 396 √6

问题6.找到的价值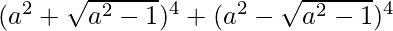$(a^2 + \sqrt{a^2-1})^4 + (a^2 - \sqrt{a^2-1})^4$ 。

解决方案：

Using binomial theorem the expression (x+y)⁴ and (x – y)⁴, can be expanded as follows:

(x + y)⁴ = ⁴C₀ x⁴ + ⁴C₁ x³ y + ⁴C₂ x² y² + ⁴C₃ x y³ + ⁴C₄ y⁴

(x – y)⁴ = ⁴C₀ x⁴ – ⁴C₁ x³ y + ⁴C₂ x² y² – ⁴C₃ x y³ + ⁴C₄  y⁴

Now adding them,

(x + y)⁴ + (x – y)⁴ = ⁴C₀ x⁴ + ⁴C₁ x³ y + ⁴C₂ x² y² + ⁴C₃ x y³ + ⁴C₄ y⁴ + [⁴C₀ x⁴ – ⁴C₁ x³ y + ⁴C₂ x² y² – ⁴C₃ x y³ + ⁴C₄ y⁴]

(x + y)⁴ + (x – y)⁴ = 2[⁴C₀ x⁴ + ⁴C₂ x² y² + ⁴C₄ y⁴]

Substituting x = a² and y = $\sqrt{a^2-1}$, we get

$(a^2 + \sqrt{a^2-1})^4 + (a^2 - \sqrt{a^2-1})^4 = 2[(a^2)^4 +6 (a^2)^2 (\sqrt{a^2-1})^2 + (\sqrt{a^2-1})^4]$

= 2[a⁸ + 6a⁴ (a²-1) + (a²-1)²]

= 2[a⁸ + 6a⁶ – 6a⁴ + (a⁴ + 1 – 2(a²)(1))]

= 2[a⁸ + 6a⁶ – 6a⁴ + a⁴ + 1 – 2a²]

= 2a⁸ + 12a⁶ – 10a⁴ – 4a² + 2

问题7。使用展开的前三个项来找到(0.99) ^{5的近似值。}

解决方案：

To make 0.99 in binomial form,

0.99 = 1 – 0.01

Now by applying binomial theorem, we get

(0. 99)⁵ = (1 – 0.01)⁵

Taking first three terms of its expansion, we have

= ⁵C₀ (1)⁵ – ⁵C₁ (1)⁴ (0.01) + ⁵C₂ (1)³ (0.01)²

= 1 – 5 (0.01) + 10 (0.01)²

= 1 – 0.05 + 0.001

= 0.951

Approximation of (0.99)⁵ = 0.951.

问题8.如果n的展开式中从开始算起的第五项与从结束算起的第五项之比，求n $(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n$是√6：1。

解决方案：

As, here it is said we have to calculate

(Fifth term from the beginning : Fifth term from the end) of the Binomial = $(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n$

Instead of taking fifth term from the end, lets reverse the binomial term and take it from beginning.

Fifth term from the end of binomial $(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n$ = Fifth term from the beginning $(\frac{1}{\sqrt[4]{3}}+ \sqrt[4]{2})^n$

Lets move further with this

As, we know that (r+1)^th term of (a+b)ⁿ is denoted by,

T_r+1 = ⁿCr a^n-r b^r

Fifth term from the beginning of $(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n$, 

T₅ = T₄₊₁ = ⁿC₄ $(\sqrt[4]{2})^{n-4} (\frac{1}{\sqrt[4]{3}})^4$

T₅ = ⁿC₄ $(\sqrt[4]{2})^n(\frac{1}{\sqrt[4]{2} \times \sqrt[4]{3}})^4$

T₅ = ⁿC⁴ $(\sqrt[4]{2})^n (\frac{1}{2 \times 3})$

T₅ = ⁿC₄ $(\frac{(\sqrt[4]{2})^n}{6})$ …………………………….(1)

Now, Fifth term from the beginning of $(\frac{1}{\sqrt[4]{3}}+ \sqrt[4]{2})^n$,

T₅ = T₄₊₁ = ⁿC₄ $(\frac{1}{\sqrt[4]{3}})^{n-4} (\sqrt[4]{2})^4$

T₅ = ⁿC₄ $\times \frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{\sqrt[4]{3}})^4} \times (2)$

T₅ = ⁿC₄ $\frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{3})} (2)$

T₅ = ⁿC₄ $(\frac{3}{(\sqrt[4]{3})^n}) (2)$

T₅ = ⁿC₄ $(\frac{6}{(\sqrt[4]{3})^n})$ ……………………….(2)

Now taking ratio of (1) and (2), which is equal to √6:1

$\frac{^nC_4 (\frac{(\sqrt[4]{2})^n}{6})}{^nC_4 (\frac{6}{(\sqrt[4]{3})^n})} = \sqrt{6}$

$\frac{(\sqrt[4]{2})^n \times (\sqrt[4]{3})^n}{(6\times 6)} = \sqrt{6}$

$(\sqrt[4]{6})^n = \sqrt{6} \times 36$

$6^{\frac{n}{4}} = 6^{\frac{5}{2}}$

$\frac{n}{4} = \frac{5}{2}$

n = $\frac{5\times 4}{2}$

n = 10

问题9.使用二项式定理展开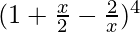$(1+\frac{x}{2} - \frac{2}{x})^4$ ，x≠0。

解决方案：

Grouping $(1+\frac{x}{2} - \frac{2}{x})^4$ in binomial form, we have

$[(1+\frac{x}{2}) - \frac{2}{x}]^4$

Comparing it with (a+b)ⁿ,

a = $(1+\frac{x}{2})$, b = $\frac{2}{x}$ and n = 4

$[(1+\frac{x}{2}) - \frac{2}{x}]^4$ = ⁴C₀ $(1+\frac{x}{2})^4$ –  ⁴C₁ $(1+\frac{x}{2})^3 (\frac{2}{x})$ + ⁴C₂ $(1+\frac{x}{2})^2 (\frac{2}{x})^2$ – ⁴C₃ $(1+\frac{x}{2}) (\frac{2}{x})^3$ + ⁴C₄ $(\frac{2}{x})^4$

= $(1+\frac{x}{2})^4 - 4 (1+\frac{x}{2})^3 (\frac{2}{x}) + 6 (1+(\frac{x}{2})^2 (\frac{4}{x^2}) - 4 (1+\frac{x}{2}) (\frac{8}{x^3}) + (\frac{16}{x^4})$

= $(1+\frac{x}{2})^4 - (\frac{8}{x}) (1+\frac{x}{2})^3 + (\frac{24}{x^2}) (1+\frac{x}{2})^2 - 4 (\frac{8}{x^3} + (\frac{x}{2})(\frac{8}{x^3})) + (\frac{16}{x^4})$

= $(1+\frac{x}{2})^4 - (\frac{8}{x}) (1+\frac{x}{2})^3 + (\frac{24}{x^2}) (1+\frac{x}{2})^2 - 4 (\frac{8}{x^3} + \frac{4}{x^2}) + (\frac{16}{x^4})$

Now, lets get the value of $(1+\frac{x}{2})^4, (1+\frac{x}{2})^3$ and $(1+\frac{x}{2})^2$

$(1+\frac{x}{2})^2 = 12 + (\frac{x}{2})^2 + 2(1)(\frac{x}{2})$

$(1+\frac{x}{2})^2 = 1 + \frac{x^2}{4} + x$

$(1+\frac{x}{2})^3$ = ³C₀ (1)³ + ³C₁ (1)² $(\frac{x}{2})$ + ³C₂ (1) $(\frac{x}{2})^2$ + ³C₃ $(\frac{x}{2})^3$

$(1+\frac{x}{2})^3 = 1 + \frac{3x}{2} + \frac{3x^2}{4} + \frac{x^3}{8}$

$(1+\frac{x}{2})^4$ = ⁴C₀ (1)⁴ + ⁴C₁ (1)³ $(\frac{x}{2})$ + ⁴C₂ (1)² $(\frac{x}{2})^2$ + ⁴C₃ (1) $(\frac{x}{2})^3$ + ⁴C₄ $(\frac{x}{2})^4$

$(1+\frac{x}{2})^4 = 1 + 2x + \frac{3x^2}{2} + \frac{x^3}{2} + \frac{x^4}{16}$

Now, substituting these values in the main equation, we get

= $1 + 2x + \frac{3x^2}{2} + \frac{x^3}{2} + \frac{x^4}{16} - (\frac{8}{x}) (1 + \frac{3x}{2} + \frac{3x^2}{4} + \frac{x^3}{8}) + (\frac{24}{x^2}) (1 + \frac{x^2}{4} + x) - 4 (\frac{8}{x^3} + \frac{4}{x^2}) + (\frac{16}{x^4})$

= $1 + 2x + \frac{3x^2}{2} + \frac{x^3}{2} + \frac{x^4}{16} - (\frac{8}{x} + (\frac{8}{x})(\frac{3x}{2}) + (\frac{8}{x})(\frac{3x^2}{4}) + (\frac{8}{x})(\frac{x^3}{8})) + (\frac{24}{x^2} + (\frac{24}{x^2})(\frac{x^2}{4}) + (\frac{24}{x^2}) (x)) - (\frac{32}{x^3} + \frac{16}{x^2}) + (\frac{16}{x^4})$

= $1 + 2x + \frac{3x^2}{2} + \frac{x^3}{2} + \frac{x^4}{16} - \frac{8}{x} - 12 - 6x - x^2 + \frac{24}{x^2} + 6+ \frac{24}{x} - \frac{32}{x^3} - \frac{16}{x^2}) + (\frac{16}{x^4})$

= $\frac{16}{x} + \frac{8}{x^2} - \frac{32}{x^3} + \frac{16}{x^4} - 4x + \frac{x^2}{2} + \frac{x^3}{2} + \frac{x^4}{16} - 5$

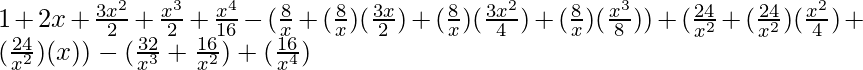
问题10.使用二项式定理求(3x ² – 2ax + 3a ² ) ^{3的展开。}

解决方案：

Grouping (3x²– 2ax + 3a²)³ in binomial form, we have

[3x² + (- 2ax + 3a²)]³

Comparing it with (a+b)ⁿ,

a = 3x², b = -a (2x-3a) and n = 3

[3x² + (-a (2x-3a))]³

= ³C₀ (3x²)³ +  ³C₁ (3x²)² (-a (2x-3a)) +  ³C₂ (3x²) (-a (2x-3a))² +  ³C₃ (-a (2x-3a))³

= 27x⁶ +  3 (9x⁴) (-a) (2x-3a) +  3 (3x²) (-a)² (2x-3a)² + (-a)³ (2x-3a)³

= 27x⁶ + (-54ax⁵ + 81a²x⁴) +  9a²x² (2x-3a)² – a³ (2x-3a)³

Now, lets get the value of (2x-3a)² and (2x-3a)³.

(2x-3a)² = (2x)² + (3a)² – 2(2x)(3a)

(2x-3a)² = 4x² + 9a² -12xa

(2x-3a)³ = (2x)³ – (3a)³ – 3(2x)(3a)(2x-3a)

(2x-3a)³ = 8x³ – 27a³ – 36x²a +54xa²

Now, substituting these values in the main equation, we get

= 27x⁶ – 54ax⁵ + 81a²x⁴ +  9a²x² (4x² + 9a² -12xa) – a³ (8x³ – 27a³ – 36x²a + 54xa²)

= 27x⁶ – 54ax⁵ + 81a²x⁴ + 36a²x⁴ + 81a⁴x² -108x³a³ – (8a³x³ – 27a⁶ – 36x²a⁴ + 54xa⁵⁾

= 27x⁶ – 54ax⁵ + 117a²x⁴ + 81a⁴x² -108x³a³ – 8a³x³ + 27a⁶ + 36x²a⁴ – 54xa⁵

= 27x⁶ – 54ax⁵+ 117a²x⁴ – 116a³x³ + 117a⁴x² – 54a⁵x + 27a⁶