11类NCERT解决方案-第11章圆锥曲线部分-练习11.3

在练习1到9中的每个练习中，找到焦点的坐标，顶点，长轴的长度，短轴的偏心率和椭圆形的直肠的长度。

问题1 $\frac{x^2}{36} + \frac{y^2}{16}$ = 1

解决方案：

Since denominator of x²/36 is larger than the denominator of y²/16,

the major axis is along the x-axis. 

On comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 36 and b² = 16

⇒ a = ±6 and b = ±4

The Foci:

Foci = (c, 0) and (-c, 0) when (a² > b²)

c = √(a² – b²)          -(when a² > b²)

c = √(36 – 16)

c = √20 = 2√5

⇒ (2√5, 0) and (-2√5, 0)

Vertices:

Vertices = (a, 0) and (-a, 0) when (a² > b²)

⇒ (6, 0) and (-6, 0)

Length of major axis:

Length of major axis = 2a (when a² > b²)

= 2 × 6

⇒ Length of major axis = 12

Length of minor axis:

Length of minor axis = 2b (when a² > b²)

= 2 × 4

⇒ Length of minor axis = 8

Eccentricity

Eccentricity = c/a (when a² > b²)

= 2√5/6

= √5/3

Length of the latus rectum:

Length of the latus rectum = 2b²/a (when a² > b²)

= 2×16/6

= 16/3

问题2。 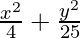$\frac{x^2}{4} + \frac{y^2}{25}$ = 1

解决方案：

Since denominator of y²/25 is larger than the denominator of x²/4, 

the major axis is along the y-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 4 and b² = 25

⇒ a = ±2 and b = ±5

The Foci:

Foci = (0, c) and (0, -c) when (a² < b²)

c = √(b² – a²)       -(when a² < b²)

c = √(25 – 4)

c = √21

⇒ (0, √21) and (0, -√21)

Vertices:

Vertices = (0, b) and (0, -b) when (a² < b²)

⇒ (0, 5) and (0, -5)

Length of major axis:

Length of major axis = 2b (when a² < b²)

= 2 × 5

⇒ Length of major axis = 10

Length of minor axis:

Length of minor axis = 2a (when a² < b²)

=2 × 2

⇒ Length of minor axis = 4

Eccentricity:

Eccentricity = c/b (when a² < b²)

= √21/5

Length of the latus rectum:

Length of the latus rectum = 2a²/b (when a² < b²)

= 2×4/5

= 8/5

问题3。 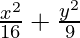$\frac{x^2}{16} + \frac{y^2}{9}$ = 1

解决方案：

Since denominator of x²/16 is larger than the denominator of y²/9, 

the major axis is along the x-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 16 and b² = 9

⇒ a = ±4 and b = ±3

The Foci:

Foci = (c, 0) and (-c, 0) when (a² > b²)

c = √(a² – b²)       -(when a² > b²)

c = √(16 – 9)

c = √7

⇒ (√7, 0) and (-√7, 0).

Vertices:

Vertices = (a, 0) and (-a, 0) when (a² > b²)

⇒ (4,0) and (-4,0)

Length of major axis:

Length of major axis = 2a (when a² > b²)

= 2 × 4

⇒ Length of major axis = 8

Length of minor axis:

Length of minor axis = 2b (when a² > b²)

= 2 × 3

⇒ Length of minor axis = 6

Eccentricity:

Eccentricity = c/a (when a²>b²)

= √7/4

Length of the latus rectum:

Length of the latus rectum = 2b²/a (when a² > b²)

= 2 × 9/4

= 9/2

问题4。 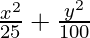$\frac{x^2}{25} + \frac{y^2}{100}$ = 1

解决方案：

Since denominator of y²/100 is larger than the denominator of x²/25, 

the major axis is along the y-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 25 and b² = 100

⇒ a = ±5 and b = ±10

The Foci:

Foci = (0, c) and (0, -c) when (a² < b²)

c = √(b² – a²)       -(when a² < b²)

c = √(100 – 25)

c = √75

c = 5√3

⇒ (0, 5√3) and (0, -5√3)

Vertices:

Vertices = (0, b) and (0, -b) when (a² < b²)

⇒ (0, 10) and (0, -10)

Length of major axis:

Length of major axis = 2b (when a² < b²)

= 2 × 10

⇒ Length of major axis = 20

Length of minor axis:

Length of minor axis = 2a (when a² < b²)

= 2 × 5

⇒ Length of minor axis = 10

Eccentricity:

Eccentricity = c/b (when a² < b²)

= 5√3/10

= √3/2

Length of the latus rectum:

Length of the latus rectum = 2a²/b (when a² < b²)

= 2 × 25/10

= 5

问题5 $\frac{x^2}{49} + \frac{y^2}{36}$ = 1

解决方案：

Since denominator of x²/49 is larger than the denominator of y²/36, 

the major axis is along the x-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 49 and b² = 36

⇒ a = ±7 and b = ±6

The Foci:

Foci = (c, 0) and (-c, 0) when (a² > b²)

c = √(a² – b²)       -(when a² > b²)

c = √(49 – 36)

c = √13

⇒ (√13, 0) and (-√13, 0).

Vertices:

Vertices = (a, 0) and (-a, 0) when (a² > b²)

⇒ (7, 0) and (-7, 0)

Length of major axis:

Length of major axis = 2a (when a² > b²)

= 2 × 7

⇒ Length of major axis = 14

Length of minor axis:

Length of minor axis = 2b (when a² > b²)

= 2 × 6

⇒ Length of minor axis = 12

Eccentricity:

Eccentricity = c/a (when a² > b²)

= √13/7

Length of the latus rectum:

Length of the latus rectum = 2b²/a (when a² > b²)

= 2 × 36/7

= 72/7

问题6。 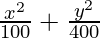$\frac{x^2}{100} + \frac{y^2}{400}$ = 1

解决方案：

Since denominator of y²/400 is larger than the denominator of x²/100, 

the major axis is along the y-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 100 and b² = 400

⇒ a = ±10 and b = ±20

The Foci:

Foci = (0, c) and (0, -c) when (a² < b²)

c = √(b² – a²)       -(when a² < b²)

c = √(400 – 100)

c = √300

c = 10√3

⇒ (0, 10√3) and (0, -10√3)

Vertices:

Vertices = (0, b) and (0, -b) when (a² < b²)

⇒ (0, 20) and (0, -20)

Length of major axis:

Length of major axis = 2b (when a² < b²)

= 2 × 20

⇒ Length of major axis = 40

Length of minor axis:

Length of minor axis = 2a (when a² < b²)

= 2 × 10

⇒ Length of minor axis = 20

Eccentricity:

Eccentricity = c/b (when a² < b²)

= 10√3/20

= √3/2

Length of the latus rectum:

Length of the latus rectum = 2a²/b (when a² < b²)

= 2×100/20

= 10

问题7. 36x ² + 4y ² = 144

解决方案：

36x² + 4y² = 144

Dividing LHS and RHS by144,

$\frac{36x^2}{144} + \frac{4y^2}{144} = \frac{144}{144}$

$\frac{x^2}{4} + \frac{y^2}{36}$ = 1 (Obtained Equation)

Since denominator of y²/36 is larger than the denominator of x²/4, 

the major axis is along the y-axis.

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 4 and b² = 36

⇒ a = ±2 and b = ±6

The Foci:

Foci = (0, c) and (0, -c) when (a² < b²)

c = √(b² – a²)      -(when a² < b²)

c = √(36 – 4)

c = √32

c = 4√2

⇒ (0, 4√2) and (0, -4√2)

Vertices:

Vertices = (0, b) and (0, -b) when (a² < b²)

⇒ (0, 6) and (0, -6)

Length of major axis:

Length of major axis = 2b (when a²2)

= 2 × 6

⇒ Length of major axis = 12

Length of minor axis

Length of minor axis = 2a (when a² < b²)

= 2 × 2

⇒ Length of minor axis = 4

Eccentricity:

Eccentricity = c/b (when a² < b²)

= 4√2/6

= 2√2/3

Length of the latus rectum:

Length of the latus rectum = 2a²/b (when a² < b²)

= 2 × 4/6

= 4/3

问题8. 16x ² + y ² = 16

解决方案：

16x² + y² = 16

Dividing LHS and RHS by16,

$\frac{16x^2}{16} + \frac{y^2}{16} = \frac{16}{16}$

$\frac{x^2}{1} + \frac{y^2}{16}$ = 1 (Obtained Equation)

Since denominator of y²/16 is larger than the denominator of x²/1, 

the major axis is along the y-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 1 and b² = 16

⇒ a = ±1 and b = ±4

The Foci: 

Foci = (0, c) and (0, -c) when (a² < b²)

c = √(b² – a²)       -(when a² < b²)

c = √(16 – 1)

c = √15

⇒ (0, √15) and (0, -√15)

Vertices:

Vertices = (0, b) and (0, -b) when (a² < b²)

⇒ (0, 4) and (0, -4)

Length of major axis:

Length of major axis = 2b (when a² < b²)

= 2 × 4

⇒ Length of major axis = 8

Length of minor axis:

Length of minor axis = 2a (when a² < b²)

=2 × 1

⇒ Length of minor axis = 2

Eccentricity:

Eccentricity = c/b (when a² < b²)

= √15/4

Length of the latus rectum:

Length of the latus rectum = 2a²/b (when a² < b²)

= 2 × 1/4

= 1/2

问题9. 4x ² + 9y ² = 36

解决方案：

4x² + 9y² = 36

Dividing LHS and RHS by 36,

$\frac{4x^2}{36} + \frac{9y^2}{36} = \frac{36}{36}$

$\frac{x^2}{9} + \frac{y^2}{4}$ = 1 (Obtained Equation)

Since denominator of x²/9 is larger than the denominator of y²/4, 

the major axis is along the x-axis. 

Comparing the given equation with $\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, we get

a² = 9 and b² = 4

⇒ a = ±3 and b = ±2

The Foci:

Foci = (c, 0) and (-c, 0) when (a² > b²)

c = √(a² – b²)      -(when a² > b²)

c = √(9 – 4)

c = √5

⇒ (√5, 0) and (-√5, 0).

Vertices

Vertices = (a, 0) and (-a, 0) when (a² > b²)

⇒ (3, 0) and (-3, 0).

Length of major axis

Length of major axis = 2a (when a² > b²)

= 2 × 3

⇒ Length of major axis = 6

Length of minor axis

Length of minor axis = 2b (when a² > b²)

= 2 × 2

⇒ Length of minor axis = 4

Eccentricity

Eccentricity = c/a (when a² > b²)

= √5/3

Length of the latus rectum

Length of the latus rectum = 2b²/a (when a² > b²)

= 2 × 4/3

= 8/3

在以下每个练习10至20中，找到满足给定条件的椭圆方程：

问题10.顶点(±5，0)，焦点(±4，0)。

解决方案：

Since the vertices are on x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that a = ±5, c = ±4

As, from the relation

c² = a² – b² (when a² > b²)

b² = a² – c²

b² = 25 – 16

b² = 9

So, a² = 25 and b² = 9

Hence, the required equation of ellipse,

$\frac{x^2}{25} + \frac{y^2}{9}$ = 1

问题11.顶点(0，±13)，焦点(0，±5)。

解决方案：

Since the vertices are on y-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where b is the semi-major axis. (where a² < b²)

Given that b = ±13, c = ±5

As, from the relation

c² = b² – a² (when a² < b²)

a² = b² – c²

a² = 169 – 25

a² = 144

So, a² = 144 and b² = 169

Hence, the required equation of ellipse,

$\frac{x^2}{144} + \frac{y^2}{169}$ = 1

问题12.顶点(±6，0)，焦点(±4，0)。

解决方案：

Since the vertices are on x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that a = ±6, c = ±4

As, from the relation

c² = a² – b² (when a² > b²)

b² = a² – c²

b² = 36 – 16

b² = 20 

So, a² = 36 and b² = 20

Hence, the required equation of ellipse,

$\frac{x^2}{36} + \frac{y^2}{20}$ = 1

问题13.长轴的末端(±3，0)，短轴的末端(0，±2)。

解决方案：

Since the major axis are on x-axis, and minor axis on the y-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that a = ±3, b = ±2

So, a² = 9 and b² = 4

Hence, the required equation of ellipse,

$\frac{x^2}{9} + \frac{y^2}{4}$ = 1

问题14.长轴的末端(0，±√5)，短轴的末端(±1，0)。

解决方案：

Since the major axis are on y-axis, and minor axis on the x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where b is the semi-major axis. (where a² < b²)

Given that a = ±1, b = ±√5

So, a² = 1 and b² = 5

Hence, the required equation of ellipse,

$\frac{x^2}{1} + \frac{y^2}{5}$ = 1

问题15。主轴26的长度，焦点(±5，0)。

解决方案：

Since the foci are on x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that c = ±5 and Length of major axis = 26

As, Length of major axis = 2a (when a² > b²)

2a = 26

a = 13

As, from the relation

c² = a² – b² (when a² > b²)

b² = a² – c²

b² = 169 – 25

b² = 144

So, a² = 169 and b² = 144

Hence, the required equation of ellipse,

$\frac{x^2}{169} + \frac{y^2}{144}$ = 1

问题16.短轴16的长度，焦点(0，±6)。

解决方案：

Since the foci are on y-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where b is the semi-major axis. (where a² < b²)

Given that c = ±6 and Length of minor axis = 16

As, Length of minor axis = 2a (when a² < b²)

2a = 16

a = 8

As, from the relation

c² = b² – a² (when a² < b²)

b² = c² + a²

b² = 36 + 64

b² = 100 

So, a² = 64 and b² = 100

Hence, the required equation of ellipse,

$\frac{x^2}{64} + \frac{y^2}{100}$ = 1

问题17.焦点(±3，0)，a = 4。

解决方案：

Since the foci are on x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that a = 4 and c = ±3

As, from the relation

c² = a² – b² (when a² > b²)

b² = a² – c²

b² = 16 – 9

b² = 7

So, a² = 16 and b² = 7

Hence, the required equation of ellipse,

$\frac{x^2}{16} + \frac{y^2}{7}$ = 1

问题18：b = 3，c = 4，原点居中； x轴上的焦点。

解决方案：

Since the foci are on x-axis, the equation will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1, where a is the semi-major axis. (where a² > b²)

Given that b = 3 and c = 4

As, from the relation

c² = a² – b² (when a² > b²)

a² = b² + c²

a² = 9 + 16

a² = 25

So, a² = 25 and b² = 9

Hence, the required equation of ellipse,

$\frac{x^2}{25} + \frac{y^2}{9}$ = 1

问题19.以(0,0)为中心，y轴为长轴，并经过点(3，2)和(1，6)。

解决方案：

The standard equation of ellipse having centre (0, 0) will be of the form 

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1

Since the points (3, 2) and (1, 6) lie on the ellipse, we can have 

$\frac{3^2}{a^2} + \frac{2^2}{b^2}$ = 1 

$\frac{9}{a^2} + \frac{4}{b^2}$ = 1         -(1)

$\frac{1^2}{a^2} + \frac{6^2}{b^2}$ = 1 

$\frac{1}{a^2} + \frac{36}{b^2}$ = 1        -(2)

Eq(2) subtracted from (multiplying eq(1) by 9) and, we get

9×($\frac{9}{a^2} + \frac{4}{b^2}$) – ($\frac{1}{a^2} + \frac{36}{b^2}$) = 9 – 1

$\frac{81}{a^2} + \frac{36}{b^2} - \frac{1}{a^2} - \frac{36}{b^2}$ = 8

80/a² = 8

a² = 80/8

a² = 10

Now, substituting a² = 10 in eq(1)

$\frac{9}{a^2} + \frac{4}{b^2}$ = 1

9/10 + 4/b² = 1

4/b² = 1 – 9/10

4/b² = 1/10

b² = 10 × 4 = 40

So, a² = 10 and b² = 40

Hence, the required equation of ellipse,

$\frac{x^2}{10} + \frac{y^2}{40}$ = 1

问题20.长轴在x轴上并穿过点(4，3)和(6，2)。

解决方案：

The standard equation of ellipse having centre (0, 0) will be of the form

$\frac{x^2}{a^2} + \frac{y^2}{b^2}$ = 1

Since the points (4,3) and (6,2) lie on the ellipse, we can have

$\frac{4^2}{a^2} + \frac{3^2}{b^2}$ = 1

$\frac{16}{a^2} + \frac{9}{b^2}$ = 1         -(1)

and, $\frac{6^2}{a^2} + \frac{2^2}{b^2}$ = 1

$\frac{36}{a^2} + \frac{4}{b^2}$ = 1         -(2)

(multiplying eq(2) by 9) subtracted from (multiplying eq(1) by 4) and, we get

9×($\frac{36}{a^2} + \frac{4}{b^2}$ ) – 4×($\frac{16}{a^2} + \frac{9}{b^2}$) = 9 – 4

$\frac{324}{a^2} + \frac{36}{b^2} - \frac{64}{a^2} - \frac{36}{b^2}$ = 5

260/a² = 5

a² = 260/5

a² = 52

Now, substituting a² = 52 in eq(1)

$\frac{16}{2} + \frac{9}{b^2}$ = 1

9/b² = 1 – 16/52

9/b² = 36/52

9/b² = 36/52

b² = 9 × 36/52 = 13

So, a² = 52 and b² = 13

Hence, the required equation of ellipse,

$\frac{x^2}{52} + \frac{y^2}{13}$ = 1