第11类RD Sharma –第20章几何级数-练习20.4

问题1.1求以下无穷级数的和： $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞$

解决方案：

Given series: $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞$

It is in the form of Geometric progression where first term=1 and common ratio=-1/3

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$ where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

       S=$\frac1{1-{(-\frac13)}}$

         =$\frac1{1+\frac13}$

        =3/4

Thus, $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞=3/4$

问题1.2找出以下无穷级数的总和： $8+4\sqrt2+4+..........∞$

解决方案：

Given series $8+4\sqrt2+4+..........∞$

It is in the form of Geometric progression where first term=8 and common ratio=1/√2

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

 S=$\frac8{1-{\frac1{\sqrt2}}}$

   =$\frac{8\sqrt2}{\sqrt2-1}$

  = 8√2(√2+1)

 =16+8√2

Thus, $8+4\sqrt2+4+..........∞$=16+8√2

问题1.3求以下无穷级数的总和： $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞$

解决方案：

Given series $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞$

⇒$(\frac25+\frac2{5^3}+......∞)+(\frac3{5^2}+\frac3{5^4}+.....∞)$

These two equations are in the form of Geometric progression

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

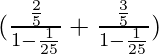
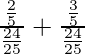
S=$(\frac{\frac25}{1-\frac1{25}}+\frac{\frac35}{1-\frac1{25}})$

 =$\frac{\frac25}{\frac{24}{25}}+\frac{\frac35}{\frac{24}{25}}$

 =$\frac1{\frac{24}{25}}$

 =25⁄24

Thus, $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞=\frac{25}{24}$

问题1.4找到以下无穷级数的和： 10-9 + 8.1-7.29 +……….∞

解决方案：

  Given series: 10-9+8.1-7.29+……….∞

⇒  $10-9+\frac{81}{10}-\frac{729}{100}+........ ∞$

The above series are in Geometric Progression with first term=10 and common ratio=-9⁄10

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

⇒ S=$\frac{10}{1-(-\frac{9}{10})}$

⇒ S=100⁄19

Thus $10-9+8.1-7.29+..........∞=\frac{100}{19}$

问题1.5求以下无穷级数的和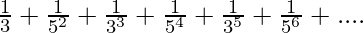： $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞$

解决方案：

Given series: $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞$

         ⇒ $(\frac13+\frac1{3^3}+\frac1{3^5}+....∞)+(\frac1{5^2}+\frac1{5^4}+....∞)$

 These two equations are in the form of Geometric progression

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

          ⇒ $(\frac{\frac13}{1-\frac1{3^2}}+\frac{\frac1{5^2}}{1-\frac1{5^2}})$

         ⇒ $(\frac{\frac13}{\frac8{3^2}}+\frac{\frac1{5^2}}{\frac{24}{5^2}})$

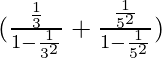
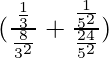
        ⇒ 3⁄8+1⁄24

        ⇒ 10⁄24

Thus, $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞=\frac{10}{24}$

问题2：证明$(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)$

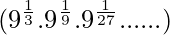
解决方案：

Let us consider left hand side of the given equation

 ⇒ $(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)$

 ⇒ $9^{\frac13+\frac19+\frac1{27}....∞}$

   The equation $\frac13+\frac19+\frac1{27}....∞$ is in the form of Geometric progression where first term=1⁄3 and common ratio=1⁄3

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

   ⇒ $9^{\frac{\frac13}{1-\frac13}}$

   ⇒ $9^{\frac12}$

   ⇒ 3= Right hand side of the given equation

Thus we proved that $(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)=3$

问题3：证明$(2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞)=2$

解决方案：

Let us consider left hand side of the given equation

let S= $2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞$

S=$2^{\frac14+\frac28+\frac3{16}+....∞}$

Denoting the terms in power with x

x=$\frac14+\frac28+\frac3{16}+.......∞$         eq-(1)

We can clearly see that this equation is neither in GP nor in AP. But the numerator of this equation is in AP and denominator in GP

let us multiply (1) with 1/2

$\frac12x=\frac12[\frac14+\frac28+\frac3{16}+.....∞]$           eq-(2)

Let us subtract (2) from (1)

$x-\frac{x}2=[\frac14+\frac28+\frac3{16}+....∞]-[\frac18+\frac2{16}+\frac3{32}+...∞]$

    $\frac{x}2=\frac14+(\frac28-\frac18)+(\frac3{16}-\frac2{16})+...∞$

    $\frac{x}2=\frac14+\frac18+\frac1{16}+...∞$

      x=$\frac12+\frac14+\frac18+....∞$

This equation is in the form of Geometric progression where first term=1/2 and common ratio=1/2

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

⇒  x=$\frac{\frac12}{1-\frac12}$

⇒  x=$\frac{\frac12}{\frac12}$

⇒ x=1

⇒S=2=Right hand side of the equation

Thus we proved that $(2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞)=2$

问题4：如果S _p表示级数1 + r ^p + r ^2p +…….∞的和，而s _p表示级数1 – r ^p + r ^2p +…….∞的和。证明S _p + s _p = 2S _2p。

解决方案：

Given S_p=1+r^p+r^2p+…….∞

The above equation is in Geometric progression where first term=1 and common ratio=r^p

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio where r<1

Thus, on substituting the value of a and r in that formula

here |r|<1 ⇒|r^p|<1

S_p=$\frac1{1-r^p}$         eq-(1)

and  s_p=1 – r^p+r^2p+…….∞

The above equation is in Geometric progression where first term=1 and common ratio=-r^p

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio where r<1

Thus, on substituting the value of a and r in that formula

here |r|<1 ⇒|r^p|<1

s_p=$\frac1{1+r^p}$          eq-(2)

on adding (1) and (2)

S_p+s_p=$\frac1{1-r^p}+\frac1{1+r^p}$

         = $\frac{1-r^p+1+r^p}{(1-r^p)(1+r^p)}$

         =$\frac2{1-(r^p)^2}$

        =$\frac2{1-r^{2p}}$                eq-(3)

From (1) We can write $\frac1{1-r^{2p}}$=S_2p

From (3), we can write that S_p+s_p=2S_2p

Hence proved.

问题5：求出一个无限递减的GP的总和，其中所有项均为正，第一项为4，第三项与第五项之差等于32⁄81

解决方案：

Let a denote the first term of G.P and r be the common ratio

we know that nth term of a G.P is given by a_n=ar^n-1

Given a=4 and a₅-a₃=$\frac{32}{81}$

Here a₅=4r⁴, a₃=4r²

⇒ 4r⁴-4r²=32⁄81

⇒  4r²(r²-1)=32⁄81

⇒ r²(r²-1)=8⁄81

let x=r²

⇒ x(x-1)=8⁄81

⇒ 81x²-81x-8=0

by using the formula of quadratic equation to solve the above equation, we get 

 x= $\frac{-(-81)\pm\sqrt{(81)^2-4(-8)(-81)}}{162}$

⇒ x=$\frac{81\pm\sqrt{6561-2592}}{162}$

⇒ x=18⁄162 or x=144⁄162

⇒ x=1⁄9  or x=8⁄9

⇒ r²=1⁄9  or r²=8⁄9

⇒ r=1⁄3  or r=2√2/3

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Let us take 1st case a=4 and r=1⁄3

Then, S=$\frac4{1-\frac13}$

⇒ S=6

Now, in 2nd case a=4 and r=$\frac{2\sqrt{2}}3$

Then, S=$\frac4{1-\frac{2\sqrt2}3}$

⇒ S=$\frac{12}{3-2\sqrt2}$

Thus the sum of the terms of an infinite decreasing G.P in which all the terms are positive are 6 and $\frac{12}{3-2\sqrt2}$

问题6：将循环十进制表示为0.125125125…。作为一个有理数。

解决方案：

Let x=0.125125125……            eq-(1)

Here 125 is the repeating term 

so,let us multiply both sides of the equation with a number such that complete repetitive part of number comes after decimal.

let us multiply (1) with 1000 in both sides ,we get

1000x=125.125125125……               eq-(2)

let us subtract (1) from (2)

1000x-x=125.0000

999x=125

   x=125⁄999

Thus, 0.125125125…. can be expressed as 125/999

问题7：找到其十进制扩展为的有理数$0.42\bar{3}$

解决方案：

Let x=0.423333333…………             eq-(1)

here 3 is the repeating part .

So let us multiply both sides of equation (1) with a number such that complete repetitive part comes after decimal

Let us multiply (1) with 100

100x =42.33333……….          eq-(2)

let us subtract (1) from (2) 

100x-x=(42.3333333………..)-(0.4233333….)

  99x =41.91

     x=41.91/99

   x=4191/9900

The rational number whose decimal expansion is $0.42\bar{3}$ is 4191/9900

问题8-1：查找具有以下十进制扩展数的有理数为$0.\bar3$

解决方案：

let x=0.333333333333………..

    x=0.3+0.03+0.003+………∞

   x=3(0.1+0.01+0.001+……..∞)

  x=$3(\frac1{10}+\frac1{100}+\frac1{1000}+......∞)$

The above equation is in Geometric Progression with common ratio=1⁄10 and first term=1⁄10

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

  x=$3(\frac{\frac1{10}}{1-{\frac1{10}}})$

  x=3×1⁄9

  x=1⁄3

The rational number having decimal expansion is $0.\bar3$ is 1⁄3

问题8-2：找到具有以下十进制扩展数的有理数为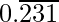$0.\overline{231}$

解决方案：

let x=0.231231231……….          eq-(1)

     x=0.231+0.000231+0.000000231+……..∞

    x=231(0.001+0.00001+0.0000001+……∞)

    x=$231(\frac1{10^3}+\frac1{10^6}+\frac1{10^9}+....∞)$

The above equation is in the form of Geometric Progression with first term=1⁄1000 common ratio=1⁄1000

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

   x=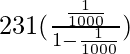$231(\frac{\frac1{1000}}{1-\frac1{1000}})$

     =$231(\frac1{999})$

     x=231/999

The rational number having decimal expansion is $0.\overline{231}$ is 231/999

问题8-3：查找具有以下十进制扩展数的有理数为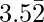$3.5\bar{2}$

解决方案：

let x=3.5222222……..

     x=3.5+0.02+0.002+0.0002+…….∞

     x=3.5+2(0.01+0.001+0.0001+…………∞)

let s= 0.01+0.001+0.0001+…………∞

    s=$\frac1{100}+\frac1{1000}+\frac1{10000}+........∞$

The above equation is in the form of Geometric Progression with first term=1⁄100 and common ratio=1⁄10

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

    s=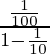$\frac{\frac1{100}}{1-\frac1{10}}$

     s =1⁄90

x=3.5+2s

  =3.5+2×1⁄90

  =35⁄10+1⁄45

  =(315+2)/90

  =317/90

The rational number having decimal expansion is $3.5\bar{2}$ is 317/90.

问题8-4：查找具有以下十进制扩展数的有理数为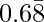$0.6\bar8$

解决方案：

let x=0.688888……….

    x=0.6+0.08+0.008+0.0008+0.00008+…….∞

   x=0.6+8(0.01+0.001+0.0001+……..∞)

let s=0.01+0.001+0.0001+………∞

    s=$\frac1{100}+\frac1{1000}+\frac1{10000}+......∞$

The above equation is in the form of Geometric Progression with first term= 1⁄100 and common ratio=1⁄10  

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

Thus, on substituting the value of a and r in that formula

 s=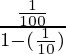$\frac{\frac1{100}}{1-(\frac1{10})}$

  =1⁄90

x=0.6+8s

 =0.6+8×1⁄90

 =62⁄90

The rational number having decimal expansion is $0.6\bar8$ is 62/90

问题9：等边三角形的一侧是18厘米。边的中点被连接形成另一个三角形，其中点又被连接形成另一个三角形。该过程将无限期继续。求出所有三角形的(i)周长之和(ii)所有三角形的面积。

解决方案：

According to Mid-Point Theorem, the sides of each triangle formed by joining the midpoints of an equilateral triangle are half of the sides of the equilateral triangle.

Thus, the sides of equilateral triangles formed are 18cm,9cm,4.5cm,2.25cm,…………….

i) Sum of perimeters of all the triangles

Let Sum of perimeters of all the triangles be P

P=3×18+3×9+3×4.5+3×2.25+………….∞

  =3(18+9+9/2+9/4+……….∞)

It is in the form of G.P with first term=18 and common ratio=1⁄2

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

where a=first term and r=common ratio

P=3($\frac{18}{1-\frac12}$)

  =3(18×2)

  =3(36)=108

Thus, Sum of perimeters of all the triangles=108cms

ii) Sum of Areas of all the triangles

We know that the area of equilateral triangle =√3/4(a²)

where a is the length of the side of equilateral triangle.

Let Sum of Areas of all the triangles be A

A= √3/4(18)²+√3/4(9)²+√3/4(4.5)²+√3/4(2.25)²+…………….∞

   =√3/4((18)²+(9)²+(4.5)²+(2.25)²+…………∞)

It is in the form of G.P with first term=(18)² and common ratio=1⁄4

We know that sum of G.P terms up to infinity is S=$\frac{a}{1-r}$

A= $\frac{\sqrt3}4(\frac{18^2}{1-\frac14})$

  = (√3/3)×18²

  = 324/√3

 = 108√3 cm²

Thus the Sum of Areas of all the triangles =108√3cm²

问题10：找到一个无限GP，其第一项为1，且每一项是其后所有项的总和

解决方案：

Given first term=1

let common ratio be r

Also given each term is the sum of all the terms which follow it

⇒ a_n=[a_n+1+a_n+2+a_n+3+……………∞] ∀ n∈ N

⇒ ar^n-1=arⁿ+arⁿ⁺¹+arⁿ⁺²+……………..∞           [since there are in G.P]

⇒ r^n-1=rⁿ+rⁿ⁺¹+rⁿ⁺²+…………..∞

⇒ r^n-1=$\frac{r^n}{1-r}$

⇒ r^n-1(1-r)=rⁿ

⇒ r^n-1-rⁿ=rⁿ

⇒ r^n-1=2rⁿ

⇒ 1=2r

⇒ r=1⁄2

Now, the infinite series will be a,ar,ar²,ar³………..∞

And thus the infinite G.P is 1,1⁄2,1⁄4,1⁄8,………………….∞

问题11：无限GP的前两个项之和为5，每个项是后续项之和的三倍。找到GP

解决方案：

Let the first term be a and common difference be r in a given infinite G.P

Given a₁+a₂=5

⇒ a+ar=5     -(i)

Also, Given, a_n=3[a_n+1+a_n+2+a_n+3+………∞] ∀ n∈ N

 ⇒ ar^n-1=3[ar^n+1-1+ar^n+2-1+ar^n+3-1+………..∞]

            =3[arⁿ+arⁿ⁺¹+arⁿ⁺²+………….∞]

           =3arⁿ[1+r+r²+………….∞]

           =3arⁿ\frac1{1-r}

  ar^n-1=3arⁿ\frac1{1-r}

  ⇒ r^-1=3⁄1-r

  ⇒ 1-r=3r

  ⇒ 1=4r

 ⇒ r=1⁄4

On substituting the value of r in (i)

 ⇒ a+a(1⁄4)=5

 ⇒ a(1+1⁄4)=5

 ⇒ a(5⁄4)=5

 ⇒ a=4

Now, the G.P terms will be a,ar,ar²,ar³,……………∞

Thus, the G.P terms will be 4,1,1⁄4,1⁄16…………∞

问题12：表明在具有公共比率r(| r | <1)的无限GP中，每个项与跟随其后的所有项之和具有恒定的比率。

解决方案：

Let us Consider a infinite G.P series whose terms are a₁,a₂,a₃,a₄,a₅…………∞ and common ratio r(|r|<1).

Also, let us assume the sum of all terms following each term will be S₁,S₂,S₃,S₄………….∞

we know that 1+r+r²+r³+r⁴+……………..∞=1⁄1-r

Now,S₁=$\frac{a_2}{1-r}$=$\frac{ar}{1-r}$

S₂=$\frac{a_3}{1-r}$=$\frac{ar^2}{1-r}$

S₃=$\frac{a_4}{1-r}$=$\frac{ar^3}{1-r}$

⇒ a₁/S₁=$\frac{a}{\frac{ar}{(1-r)}}$=(1-r)/r

⇒a₂/S₂=$\frac{ar}{\frac{ar^2}{(1-r)}}$=(1-r)/r

⇒ a₃/S₃=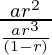$\frac{ar^2}{\frac{ar^3}{(1-r)}}$=(1-r)/r

We can clearly observe that a_n/S_n=constant

Thus, we proved that ratio of each term to the sum of all the terms that follow it are constant.

问题13：如果S表示无穷GP的和S ₁表示其项的平方和，则证明第一项和公比分别为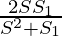$\frac{2SS_1}{S^2+S_1}$和$\frac{S^2-S_1}{S^2+S_1}$

解决方案：

Let us consider an infinite G.P series 

let a be the first term and r be the common ratio in G.P series.

Given

 a+ar+ar²+ar³+…………..∞=S

⇒ a(1+r+r²+r³+…………..∞)=S

⇒ a(1⁄1-r)=S                          eq-(1)

Also Given

S₁=a²+a²r²+a²r⁴+…………..∞

   =a²(1+r²+r⁴+………….∞)

   =a²($\frac1{1-r^2}$)

    =$\frac{a}{1+r}$×$\frac{a}{1-r}$

   S₁=S×($\frac{a}{1+r}$)                   eq-(2)

Divide (2) by (1)

S₁/S= $\frac{\frac{aS}{1+r}}{\frac{a}{1-r}}$

       =$\frac{S}{\frac{1+r}{1-r}}$

  $\frac{S_1}{S^2}=\frac{1-r}{1+r}$ 

⇒ (1-r)S²=(1+r)S₁

⇒ S²-S₁=r(S²+S₁)

⇒ r=$\frac{S^2-S_1}{S^2+S_1}$

On substituting the value of r in (1)

S= $\frac{a}{1-\frac{{S^2-S_1}}{{S^2+S_1}}}$

S = $\frac{a{(S^2+S_1)}}{S^2+S_1-(S^2-S_1)}$

 S= $\frac{a(S^2+S_1)}{2S_1}$

2SS₁=a(S²+S₁)

⇒ a=$\frac{2SS_1}{S^2+S_1}$

Thus, we proved that a=$\frac{2SS_1}{S^2+S_1}$ and r=$\frac{S^2-S_1}{S^2+S_1}$