Class 11 RD Sharma解决方案–第20章几何级数-练习20.5 |套装1

问题1.如果a，b，c在GP中，请证明日志a，log b，log c在AP中

解决方案：

Given: a, b and c are in G.P.

Using property of geometric mean, we get

b² = ac 

(b²)ⁿ = (ac)ⁿ

b²n = aⁿ cⁿ

Now, use log on both the sides, we get,

log b²ⁿ = log (aⁿcⁿ)

log (bⁿ)² = log aⁿ + log cⁿ

2 log bⁿ = log aⁿ + log cⁿ

Hence, proved log aⁿ, log bⁿ, log cⁿ are in A.P

问题2。如果a，b，c在GP中，请证明1 / log _a m，1 / log _b m，1 / log _c m在AP中

解决方案：

Given: a, b and c are in GP

Using the property of geometric mean

b² = ac 

On applying log on both sides with base m, we get

log_m b² = log_m ac

Using property of log

log_m b² = log_m a + log_m c 

2log_m b = log_m a + log_m c

2/log_b m = 1/log_a m + 1/log_c m

Hence, proved 1/log_a m, 1/log_b m, 1/log_c m are in A.P.

问题3.找出k，使得k + 9，k – 6和4构成GP的三个连续项

解决方案：

Let us considered  

a = k + 9

b = k − 6 

c = 4

AS we know that a, b and c are in GP, then

By using property of geometric mean, we get

b² = ac 

(k − 6)² = 4(k + 9)

k² – 12k + 36 = 4k + 36

k² – 16k = 0

k = 0 or k = 16

问题4. AP中有3个数字，它们的总和为15。如果分别将1、3、9加到它们上，则它们构成GP来找到这些数字。

解决方案：

Let us considered the first term of an A.P. = a  

Common difference = d

a₁ + a₂ + a₃ = 15

Here, the three number are: a, a + d, and a + 2d

So,

a + a + d + a + 2d = 15

3a + 3d = 15 or a + d = 5

d = 5 – a          -(1)

a + 1, a + d + 3, and a + 2d + 9

They are in GP, that is:

(a + d + 3)/(a + 1) = (a + 2d + 9)/(a + d + 3)

(a + d + 3)² = (a + 2d + 9)(a + 1)

a² + d² + 9 + 2ad + 6d + 6a = a² + a + 2da + 2d + 9a + 9

(5 – a)² – 4a + 4(5 – a) = 0

25 + a² – 10a – 4a + 20 – 4a = 0

a² – 18a + 45 = 0

a² – 15a – 3a + 45 = 0

a(a – 15) – 3(a – 15) = 0

a = 3 or a = 15

d = 5 – a

d = 5 – 3 or d = 5 – 15

d = 2 or – 10

Then,

For a = 3 and d = 2, A.P is 3, 5, 7

For a = 15 and d = -10, A.P is 15, 5, -5

Hence, the numbers are 3, 5, 7 or 15, 5, – 5

问题5.作为AP的连续项的三个数字之和为21。如果第二个数字减少1，第三个数字增加1，我们将获得GP的三个连续项。查找数字。

解决方案：

Let us considered the first term of an A.P. be = a

Common difference = d

a₁ + a₂ + a₃ = 21

Here, the three number are: a, a + d, and a + 2d

So,

3a + 3d = 21 or

a + d = 7.

d = 7 – a          -(1)

a, a + d – 1, and a + 2d + 1

They are now in GP, that is:

(a + d – 1)/a = (a + 2d + 1)/(a + d – 1)

(a + d – 1)² = a(a + 2d + 1)

a² + d² + 1 + 2ad – 2d – 2a = a² + a + 2da

(7 – a)² – 3a + 1 – 2(7 – a) = 0

49 + a² – 14a – 3a + 1 – 14 + 2a = 0

a² – 15a + 36 = 0

a² – 12a – 3a + 36 = 0

a(a – 12) – 3(a – 12) = 0

a = 3 or a = 12

d = 7 – a

d = 7 – 3 or d = 7 – 12

d = 4 or – 5

Then,

For a = 3 and d = 4, A.P is 3, 7, 11

For a = 12 and d = -5, A.P is 12, 7, 2

Hence, the numbers are 3, 7, 11 or 12, 7, 2

问题6. AP中三个数字a，b，c的总和为18。如果a和b分别增加4，而c增加36，则新数字构成GP查找a，b，c。

解决方案：

Let us considered the first term of an A.P. = a 

Common difference = d

b = a + d; c = a + 2d.

Given:

a + b + c = 18

3a + 3d = 18 or a + d = 6.

d = 6 – a          -(1)

a + 4, a + d + 4, and a + 2d + 36

They are now in GP, that is:

(a + d + 4)/(a + 4) = (a + 2d + 36)/(a + d + 4)

(a + d + 4)² = (a + 2d + 36)(a + 4)

a² + d² + 16 + 8a + 2ad + 8d = a² + 4a + 2da + 36a + 144 + 8d

d² – 32a – 128

(6 – a)² – 32a – 128 = 0

36 + a² – 12a – 32a – 128 = 0

a² – 44a – 92 = 0

a² – 46a + 2a – 92 = 0

a(a – 46) + 2(a – 46) = 0

a = – 2 or a = 46

d = 6 –a

d = 6 – (– 2) or d = 6 – 46

d = 8 or – 40

Then,

For a = -2 and d = 8, A.P is -2, 6, 14

For a = 46 and d = -40, A.P is 46, 6, -34

Hence, the numbers are – 2, 6, 14 or 46, 6, – 34

问题7. GP中三个数字的总和为56。如果我们从这些数字中依次减去1、7、21，我们将获得一个AP。找到这些数字。

解决方案：

Let us considered the three numbers = a, ar, ar²

a + ar + ar² = 56          -(1)

Now, subtract 1, 7, 21 from the numbers, we get,

(a – 1), (ar – 7), (ar² – 21)

The above numbers are in AP.

If three numbers are in AP, 

So, according to the arithmetic mean, we can write as 2b = a + c

2 (ar – 7) = a – 1 + ar² – 21

= (ar² + a) – 22

2ar – 14 = (56 – ar) – 22

2ar – 14 = 34 – ar

3ar = 48

ar = 48/3

ar = 16

a = 16/r          -(2)

Now, substitute the value of a in eq(1) we get,

(16 + 16r + 16r²)/r = 56

16 + 16r + 16r² = 56r

16r² – 40r + 16 = 0

2r² – 5r + 2 = 0

2r² – 4r – r + 2 = 0

2r(r – 2) – 1(r – 2) = 0

(r – 2) (2r – 1) = 0

r = 2 or 1/2

Substitute the value of r in eq(2) we get,

a = 16/r

= 16/2 or 16/(1/2)

= 8 or 32

Hence, the three numbers are (a, ar, ar²) is (8, 16, 32)

问题8.如果a，b，c在GP中，请证明：

(i)a(b2 + c ² )= c(a ² + b ² )

(ii)a ² b ² c ² [1 / a ³ + 1 / b ³ + 1 / c ³ ] = a ³ + b ³ + c ³

(iii)(a + b + c) ² /(a ² + b ² + c ² )=(a + b + c)/(a-b + c)

(iv)1 /(a ² – b ² )+ 1 / b ² = 1 /(b ² – c ² )

(v)(a + 2b + 2c)(a – 2b + 2c)= a ² + 4c ²

解决方案：

(i) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

Let LHS: a(b² + c²)

Now, on substituting b² = ac, we get

a(ac + c²)

a²c + ac²

c(a² + ac)

On Substituting ac = b² we get,

c(a² + b²) = RHS

LHS = RHS

Hence, proved.

(ii) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

Let LHS: a²b²c² [1/a³ + 1/b³ + 1/c³]

a²b²c²/a³ + a²b²c²/b³ + a²b²c²/c³

b²c²/a + a²c²/b + a²b²/c

(ac)c²/a + (b²)²/b + a²(ac)/c         -(∵ b² = ac)

ac³/a + b⁴/b + a³c/c

c³ + b³ + a³ = RHS

LHS = RHS

Hence, proved.

(iii) Given: a, b, c are in GP.

 Using the property of geometric mean,

b² = ac

Let LHS: (a + b + c)² / (a² + b² + c²)

(a + b + c)² / (a² + b² + c²) = (a + b + c)²/(a² – b² + c² + 2b²)

= (a + b + c)² / (a² – b² + c² + 2ac)      -(∵ b² = ac)

= (a + b + c)² / (a + b + c)(a – b + c)       -(∵ (a + b + c)(a – b + c) = a² – b² + c² + 2ac)

= (a + b + c) / (a – b + c)

= RHS

LHS = RHS

Hence, proved.

(iv) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

Let LHS: 1/(a² – b²) + 1/b²

On taking LCM, we get

1/(a² – b²) + 1/b² = (b² + a² – b²)/(a² – b²)b²

= a² / (a²b² – b⁴)

= a² / (a²b² – (b²)²)

= a² / (a²b² – (ac)²)        -(∵ b² = ac)

= a² / (a²b² – a²c²)

= a² / a²(b² – c²)

= 1/ (b² – c²)

= RHS

LHS = RHS

Hence, proved.

(v) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

Let LHS: (a + 2b + 2c) (a – 2b + 2c)

Now, on expanding, we get

(a + 2b + 2c) (a – 2b + 2c) = a² – 2ab + 2ac + 2ab – 4b² + 4bc + 2ac – 4bc + 4c²

= a² + 4ac – 4b² + 4c²

= a² + 4ac – 4(ac) + 4c²         -(∵ b² = ac)

= a² + 4c²

= RHS

LHS = RHS

Hence, proved.

问题9.如果a，b，c，d在GP中，请证明：

(i)(ab – cd)/(b ² – c ² )=(a + c)/ b

(ii)(a + b + c + d) ² =(a + b) ² + 2(b + c) ² +(c + d) ²

(iii)(b + c)(b + d)=(c + a)(c + d)

解决方案：

(i) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

bc = ad

c² = bd

Let LHS: (ab – cd) / (b² – c²)

(ab – cd) / (b² – c²) = (ab – cd) / (ac – bd)

= (ab – cd)b / (ac – bd)b

= (ab² – bcd) / (ac – bd)b

= [a(ac) – c(c²)] / (ac – bd)b

= (a²c – c³) / (ac – bd)b

= [c(a² – c²)] / (ac – bd)b

= [(a + c) (ac – c²)] / (ac – bd)b

= [(a + c) (ac – bd)] / (ac – bd)b

= (a + c) / b

= RHS

LHS = RHS

Hence, proved.

(ii) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

bc = ad

c² = bd

Let RHS: (a + b)² + 2(b + c)² + (c + d)²

Now, on expanding, we get

(a + b)² + 2(b + c)² + (c + d)² = (a + b)² + 2 (a + b) (c + d) + (c + d)²

= a² + b² + 2ab + 2(c² + b² + 2cb) + c² + d² + 2cd

= a² + b² + c² + d² + 2ab + 2(c² + b² + 2cb) + 2cd

= a² + b² + c² + d² + 2(ab + bd + ac + cb +cd)         -(∵ c² = bd, b² = ac)

(a + b + c)² + d² + 2d(a + b + c) = {(a + b + c) + d}²

RHS = LHS

Hence, proved.

(iii) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

bc = ad

c² = bd

Let LHS: (b + c) (b + d)

Now, on expanding, we get

(b + c) (b + d) = b² + bd + cb + cd

= ac + c² + ad + cd

= c (a + c) + d (a + c)

= (a + c) (c + d)

= RHS

LHS = RHS

Hence, proved.

问题10。如果a，b，c在GP中，请证明以下内容也在GP中：

(i)a ² ，b ² ，c ²

(ii)a ³ ，b ³ ，c ³

(iii)a ² + b ² ，ab + bc，b ² + c ²

解决方案：

(i) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

On squaring both the sides we get,

(b²)² = (ac)²

(b²)² = a²c²

Hence, proved a², b², c² are in G.P.

(ii) Given: a, b, c are in GP.

By using the property of geometric mean,

b² = ac

On squaring both the sides, we get

(b²)³ = (ac)³

(b²)³ = a³c³

(b³)² = a³c³

Hence, proved a³, b³, c³ are in G.P.

(iii) Given: a, b, c are in GP.

Using the property of geometric mean,

b² = ac

a² + b², ab + bc, b² + c² or (ab + bc)² = (a² + b²) (b² + c²) 

Let LHS: (ab + bc)²

Now, on expanding, we get

(ab + bc)² = a²b² + 2ab²c + b²c²

= a²b² + 2b²(b²) + b²c²            -(∵ ac = b²⁾

= a²b² + 2b⁴ + b²c²

= a²b² + b⁴ + a²c² + b²c²         -(∵ b² = ac)

= b²(b² + a²) + c²(a² + b²)

= (a² + b²)(b² + c²)

= RHS

LHS = RHS

Hence, a² + b², ab + bc, b² + c² are in GP.

问题11：如果GP中的a，b，c，d能够证明；

(i)(a ² + b ² )，(b ² + c ² )，(c ² + d ² )在GP中

(ii)(a ² – b ² )，(b ² – c ² )，(c ² – d ² )在GP中

(iii) 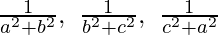$\frac{1}{a^2+b^2},\ \frac{1}{b^2+c^2},\ \frac{1}{c^2+a^2}$在GP中

(iv)(a ² + b ² + c ² )，(ab + bc + cd)，(b ² + c ² + d ² )在GP中

解决方案：

(i) Given: a, b, c, d are in G.P.

So, a, b = ar, c = ar², d = ar³

Now,

(b² + c²)² = (a² + b²)(c² + d²)

(a²r² + a²r⁴)² = (a² + a²r²)(a²r⁴ + a²r⁶)

a⁴(r² + r⁴) = a²(1 + r²)a²r⁴(1 + r²)

a⁴r⁴(1 + r²)² = a⁴r⁴(1 + r²)²

L.H.S = R.H.S

⇒ (b² + c²)² = (a² + b²)(c² + d²)

Hence, proved (a² + b²), (b² + c²), (c² + d²) are in G.P.

(ii)  Given: a, b, c, d are in G.P.

So, a, b = ar, c = ar², d = ar³

Now,

(b² – c²)² = (a² – b²)(c² – d²)

(a²r² – a²r⁴) = (a² – a²r²)(a²r⁴ – a²r⁶)

a⁴(r² – r⁴)² = a²(1 – r²) a²r⁴ (1 – r²)

a⁴r⁴ (1 – r²)² = a⁴r⁴ (1 – r²)²

L.H.S = R.H.S

⇒ (b² – c²)² = (a² – b²)(c² – d²)

Hence, proved (a² – b²), (b² – c²), (c² – d²) are in G.P.

(iii) Given: a, b, c, d are in G.P.

So, a, b = ar, c = ar², d = ar³

Now,

$\left(\frac{1}{b^2+c^2}\right)^2=\left(\frac{1}{a^2+b^2}\right)\left(\frac{1}{c^2+d^2}\right)\\ \left(\frac{1}{a^2r^2+a^2r^4}\right)^2=\left(\frac{1}{a^2+a^2r^2}\right)\left(\frac{1}{a^2r^4+a^2r^6}\right)\\ \frac{1}{a^4(r^2+r^4)}=\frac{1}{a^2(1+r^2)}\times\frac{1}{a^2(r^4+r^6)}\\ \frac{1}{a^4r^4(1+r^2)^2}=\frac{1}{a^2r^4(1+r^2)(1+r^2)}\\ \frac{1}{a^4r^4(1+r^2)^2}=\frac{1}{a^2r^4(1+r^2)^2}$

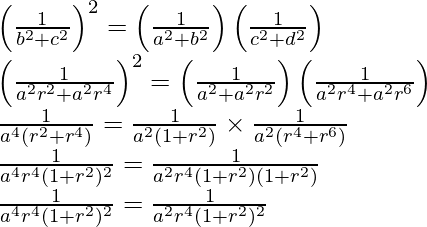
L.H.S = R.H.S

$\Rightarrow\left(\frac{1}{b^2+c^2}\right)^2=\left(\frac{1}{a^2+b^2}\right)\left(\frac{1}{c^2+d^2}\right)\\$ 

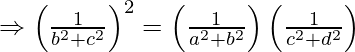
Hence, proved $(\frac{1}{a^2+b^2}),\ (\frac{1}{b^2+c^2}),(\frac{1}{c^2+d^2})$ are in G.P.

(iv) Given: a, b, c, d are in G.P.

So, a, b = ar, c = ar², d = ar³

Now,

(ab + bc + cd)² = (a² + b² + c²)(b² + c² + d²)

(a²r + a²r³ + a²r⁵)² = (a² + a²r² + a²r⁴)(a²r² + a²r⁴ + a²r⁶)

a⁴(r + r³ + r⁵)² = a²(1 + r² + r⁴) a²r² ( 1 + r² + r⁴)

a⁴r²(1 + r² + r⁴)² = a⁴r²(1 + r² + r⁴)²

L.H.S = R.H.S

⇒ (ab + bc + cd)² = (a² + b² + c²)(b² + c² + d²)

Hence, proved (a² + b² + c²), (ab + bc + cd), (b² + c² + d²) are in G.P.