问题1.画一个半径为6厘米的圆。从离中心10厘米的点开始,构造与圆的切线对并测量其长度?
解决方案:
Construction Procedure:
The construction to draw a pair of tangents to the given circle is as follows.
Step 1. Draw a circle with radius = 6 cm with centre O.
Step 2. A point P can be constructed 10 cm away from centre O.
Step 3. The points O and P are then joined to form a line
Step 4. Draw the perpendicular bisector of the line OP.
Step 5. Construct M as the mid-point of the line segment PO.
Step 6. Using M as the centre, measure the length of the line segment MO
Step 7. Now using MO as the radius, draw a circle.
Step 8. The circle drawn with the radius of MO, intersect the previous circle at point Q and R.
Step 9. Join the line segments PQ and PR.
Step 10. Now, PQ and PR are the required tangents.

理由:
The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 6cm with centre O. This can be proved by joining OQ and OR which are represented in dotted lines.
From the construction, we can see that,
∠PQO is an angle in the semi-circle.
Every angle in a semi-circle is a right angle, therefore,
∴ ∠PQO = 90°
Now,
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with a radius of 6 cm, PQ must be a tangent of the circle. Similarly, we can also prove that PR is a tangent of the circle. Hence, justified.
问题2.从半径为6 cm的同心圆上的一个点构造一个半径为4 cm的圆的切线,并测量其长度。另外,通过实际计算验证测量结果吗?
解决方案:
Construction Procedure:
For the specified circle, the tangent can be drawn as follows.
Step 1. Draw a circle of 4 cm radius with centre O.
Step 2. Taking O as the centre draw another circle of radius 6 cm.
Step 3. Locate a point P on this circle
Step 4. Join the points O and P to form a line segment OP.
Step 5. Construct the perpendicular bisector to the line OP, where M is the mid-point
Step 6. Taking M as its centre, draw a circle with MO as its radius
Step 7. The circle drawn with the radius OM, intersect the given circle at the points Q and R.
Step 8. Join the line segments PQ and PR.
Step 9. PQ and PR are the required tangents of the circle.
We can see that PQ and PR are of length 4.47 cm each.
Now, In ∆PQO,
Since PQ is a tangent,
∠PQO = 90°, PO = 6cm and QO = 4 cm
Applying Pythagoras theorem in ∆PQO, we obtain PQ2 + QO2 = PQ2
PQ2 + (4)2 = (6)2
=> PQ2 + 16 = 36
=> PQ2 = 36 − 16
=> PQ2 = 20
PQ = 2√5
PQ = 4.47 cm
Therefore, the tangent length PQ = 4.47
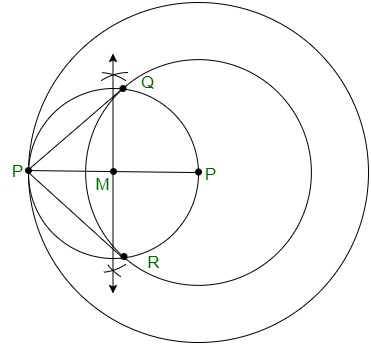
理由:
It can be proved that PQ and PR are the tangents to the circle of radius 4 cm with centre O.
Proof,
Join OQ and OR represented in dotted lines. Now,
∠PQO is an angle in the semi-circle.
Every angle in a semi-circle is a right angle, therefore, ∠PQO = 90° s.t
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with a radius of 4 cm, PQ must be a tangent of the circle. Similarly, we can prove that PR is a tangent of the circle.
问题3.画一个半径为3厘米的圆。在其延伸直径之一上取两个点P和Q,每个直径与中心的距离为7 cm 。从这两个点P和Q向圆画切线。
解决方案:
Construction Procedure:
The tangent for the given circle can be constructed as follows.
Step 1. Construct a circle with a radius of 3cm with centre O.
Step 2. Draw a diameter of a circle that extends 7 cm from the centre O of the circle and mark the endpoints as P and Q.
Step 3. Draw the perpendicular bisector of the constructed line segment PO.
Step 4. Mark the midpoint of PO as M.
Step 5. Draw another circle with M as centre and MO as its radius
Step 6. Now join the points PA and PB in which the circle with radius MO intersects the circle of circle 3cm.
Step 7. PA and PB are the required tangents of the circle.
Step 8. From that, QC and QD are the required tangents from point Q.
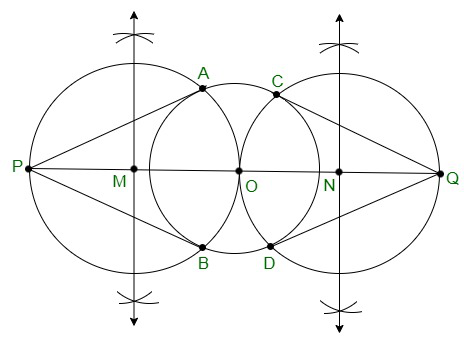
理由:
The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 3 cm with centre O.
Proof,
Join OA and OB. Now,
∠PAO is an angle in the semi-circle, which is equal to 90 degrees.
∴ ∠PAO = 90° s.t
⇒ OA ⊥ PA
Since OA is the radius of the circle with a radius of 3 cm, PA must be a tangent of the circle.
PB, QC, and QD are the tangent of the circle [by similar proof]. Hence, justified.
问题4.绘制一对切线到半径为5 cm的圆,该圆以60°的角度彼此倾斜吗?
解决方案:
Construction Procedure:
The tangents can be constructed in the following manner:
Step 1. Draw a circle with a centre O of the radius of 5 cm.
Step 2. Construct any arbitrary point Q on the circumference of the circle and join the line segment OQ.
Step 3. Also, draw a perpendicular to QP at point Q.
Step 4. Draw a radius OR, making an angle of 120° i.e(180°−60°) with OQ.
Step 5. Draw a perpendicular to the line RP at point R.
Step 6. Both the perpendicular bisectors intersect at P.
Step 7. Therefore, PQ and PR are the required tangents at an angle of 60°.

理由:
The construction can be justified by proving that ∠QPR = 60°
We have,
∠OQP = 90°, ∠ORP = 90°
Also ∠QOR = 120°
We know that, the summation of the interior angles of a quadrilateral = 360°
Substituting values,
∠OQP + ∠QOR + ∠ORP + ∠QPR = 360o
=> 90° + 120° + 90° + ∠QPR = 360°
Calculating, we get, ∠QPR = 60°
Hence, justified.
问题5.画一条长度为8厘米的线段AB。以A为中心,绘制一个半径为4 cm的圆,以B为中心,绘制另一个半径为3 cm的圆。从另一个圆的中心构造到每个圆的切线?
解决方案:
Construction Procedure:
The tangent for the given circle can be constructed as follows.
Step 1. Construct a line segment named AB = 8 cm.
Step 2. Taking A as the centre and draw a circle of a radius of 4 cm.
Step 3. Taking B as centre, draw another circle of radius 3 cm.
Step 4. Draw the perpendicular bisector of the line AB with M as the midpoint.
Step 5. Taking M as the centre, draw another circle with the radius of MA or MB which intersects the circle at the points P, Q, R, and S.
Step 6. Join the line segments AR, AS, BP, and BQ respectively.
Step 7. The required tangents are AR, AS, BP, and BQ.
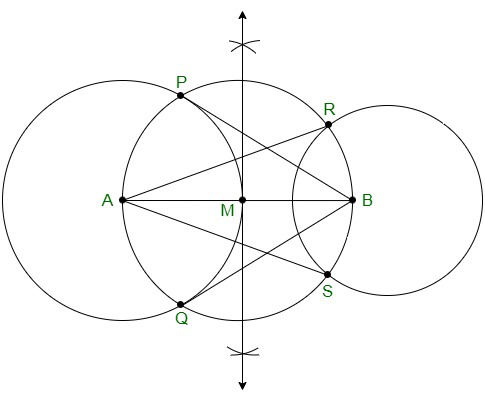
理由:
The construction can be justified by proving that AS and AR are the tangents of the circle with centre B and BP and BQ are the tangents of the circle with a circle centered at A.
Proof,
Join AP, AQ, BS, and BR.
∠ASB is an angle in the semi-circle.
∴ ∠ASB = 90°
⇒ BS ⊥ AS
Now, BS is the radius of the circle. Therefore, AS must be a tangent of the circle. Similarly, AR, BP, and BQ are the required tangents of the given circle.
问题6.假设ABC是一个直角三角形,其中AB = 6 cm,BC = 8 cm,∠B = 90°。 BD在AC上与B垂直。绘制通过B,C,D的圆。构造从A到该圆的切线?
解决方案:
Construction Procedure:
The tangent for the given circle can be constructed as follows
Step 1. Draw a line segment with base BC = 8cm
Step 2. Construct an angle of 90° at point B, s.t ∠ B = 90°.
Step 3. Taking B as centre, draw an arc of 6cm.
Step 4. Mark the point of intersection as A.
Step 5. Join the line segment AC.
Step 6. Now, we have ABC as the required triangle.
Step 7. Now, construct the perpendicular bisector to the line BC with the midpoint as E.
Step 8. Taking E as the centre, draw a circle with BE or EC as the radius.
Step 9. Join A and E to form a line segment.
Step 10. Now, again draw the perpendicular bisector to the line AE and the midpoint is taken as M
Step 11. Taking M as the centre, draw a circle with AM or ME as the radius.
Step 12. Both the circles intersect at points B and Q.
Step 13. Join points A and Q to form a line segment.
Step 14. Therefore, AB and AQ are the required tangents

理由:
The construction can be justified by proving that AG and AB are the tangents to the circle.
Proof,
Join EQ.
∠AQE is an angle in the semi-circle.
∴ ∠AQE = 90°
Now, ⇒ EQ⊥ AQ
Since EQ is the radius of the circle, AQ will be a tangent of the circle. Also, ∠B = 90°
⇒ AB ⊥ BE
Since BE is the radius of the circle, AB has to be a tangent of the circle. Hence, justified.
问题7.在手镯的帮助下画一个圆。在圆外取一点。从该点到圆构造一对切线?
解决方案:
Construction Procedure:
The required tangents can be constructed on the given circle as follows.
Step 1. Draw an arbitrary circle. Mark its centre as O.
Step 2. Draw two non-parallel chords such as AB and CD.
Step 3. Draw the perpendicular bisector of AB and CD
Step 4. Taking O as the centre where both the perpendicular bisectors AB and CD intersect.
Step 5. Take a point P outside the circle.
Step 6. Join the points O and P to form a line segment.
Step 7. Now draw the perpendicular bisector of the line PO and mark its midpoint as M.
Step 8. Taking M as centre and MO as the radius draw a circle.
Step 9. Both the circles intersect at the points Q and R.
Step 10. Now join PQ and PR.
Step 11. Therefore, PQ and PR are the required tangents.
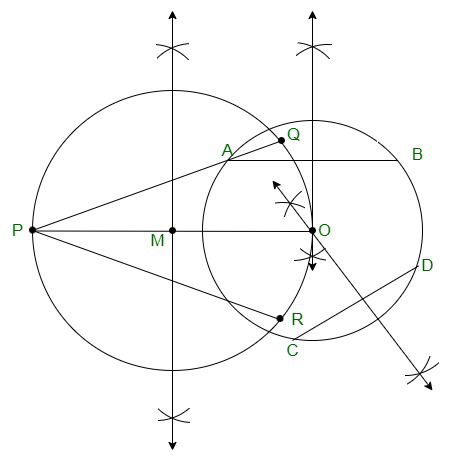
理由:
The construction can be justified by proving that PQ and PR are the tangents to the circle. The perpendicular bisector of any chord of the circle passes through the centre. Now, join the points OQ and OR.
Both the perpendicular bisectors intersect at the centre of the circle. Since ∠PQO is an angle in the semi-circle.
∴ ∠PQO = 90°
⇒ OQ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly,
∴ ∠PRO = 90°
⇒ OR ⊥ PO
Similarly, since OR is the radius of the circle, PR has to be a tangent of the circle. Therefore, PQ and PR are the tangents of a circle.